群论

一、引入

前置声明：

• 本文章讲述了群论在 OI 中的一点简单运用

• 需要一定的图论、生成函数基础

• 如果有什么建议或意见，欢迎评论、私信！！！

T1 有标号项链计数

给定正整数 \(n,m\) 求用 \(m\) 种颜色染色一个长为 \(n\) 的项链的方案数，项链不能旋转

solution

答案显然是 $m^n$

哪个项链不能旋转？？？这道题明显脱离实际好吧

T2 无标号项链计数

给定正整数 \(n,m\) 求用 \(m\) 种颜色染色一个长为 \(n\) 的项链的方案数，项链可以旋转

solution

我们可以用所有 $\lceil$旋转 $i$ 次$\rfloor$ 的操作来将所有项链 $\lceil$去重$\rfloor$，我们要问的是去重后的不同项链个数。

以 \(n=4,m=2\) 为例：

\(\lceil\)旋转一次\(\rfloor\)串成环

：

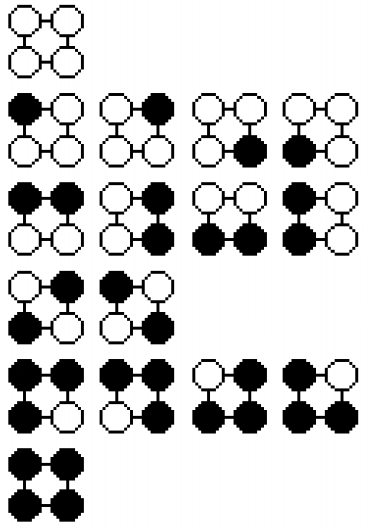
于是答案就是 \(6\)

我们于是需要一个巧妙的方法，让每个环都只算一次。

巧妙的方法：

我们对所有的项链 \(l\)，计算 旋转 \(r~(r\leq n)\) 次 后可以变成自己的 \(pair(l,r)\) 的个数

例子

将上图项链记为 \(l_1\)，那么就有 \(pair(l_1,2),pair(l_1,4)\) 满足条件

首先，我们计算对于每个项链，最少旋转 \(L\) 次可以变成自己

我们知道项链长为 \(n\)，很容易知道做 \(\exists k\in \mathbb{Z},kL = n\)，即可得到 \(L|n\)

那么一个 \(r\) 是合法的，当且仅当 \(L|r,r|n\)，那么一共就有 \(\frac n L\) 个合法的 \(r\)，而环中恰好有 \(L\) 个元素，所以每个环对答案的贡献恰好为 \(L\cdot\frac n L = n\)，计算这值后除以 \(n\) 就是答案。

然后，我们对每一个旋转 \(r\) 次的操作计算，有多少个项链 \(l\) 在 \(\lceil\)旋转\(r\)次\(\rfloor\) 的作用下不变，这就是\(\lceil\)旋转\(r\)次\(\rfloor\) 这个变换的不动点个数。

一个旋转操作会将项链分成若干个等价类，每个等价类的颜色必须相同，不同等价类间相互独立

例子

上图即为 \(n = 4,r = 2\) 时的 \(2\) 个等价类。

答案即为：

\[ans = \frac 1 n\sum\limits_{r=1}^nm^{\gcd(n,r)} \]

于是我们做到了 \(O(n)\) 的复杂度

我们需要通过上面的方法，尝试总结归纳出通用的结论。

二、基础知识

1. 群和群作用

• 群：设 \(G\) 为一个非空集合，在其中定义了一个二元运算 \(\circ\)，如果满足以下条件：
  • 封闭性：\(\forall f,g\in G,f\circ g \in G\)
  • 结合律：\(\forall f,g,h\in G,(f\circ g)\circ h = f\circ(g\circ h)\)
  • 单位元：\(\exists f\in G,\forall g\in G,g\circ e = e\circ g = g\)
  • 逆元：\(\forall f\in G,\exists g \in G,f\circ g = g\circ f = e\)，我们称 \(g\) 为 \(f\) 的逆元，记作 \(g = f^{-1}\)

注意！！！没有交换律！！！

特别地，对于满足交换律的群，我们将其称作 交换群 / 阿贝尔群

还有一类特殊的群，置换群：如果群 \(G\) 中的元素都是置换（排列），我们就称 \(G\) 为 置换群

• 染色：我们称一个 \(n\) 元数对 \(c = (c_0,c_1,\cdots,c_{n-1})\) 为一个 \(n\) 元的染色。

对于置换群众的一个置换 \(g\in G\)，我们定义它 \(\lceil\)作用\(\rfloor\) 于染色 \(c\) 上得到另一个染色 \(c'\) 式子如下：

\[g \cdot c = (c_{g_{(0)}},c_{g_{(1)}},\cdots,c_{g_{(n-1)}}) \]

例子

对于上面的T2，我们的一个项链即为一种染色

而题中的旋转即为置换：

\[\begin{Bmatrix} &\{0,1,2,3,\cdots,n-2,n-1\},\\ &\{1,2,3,4,\cdots,n-1,0\},\\ &\{2,3,4,5,\cdots,0,1\},\\ &\cdots\\ &\{n-1,0,1,2,\cdots,n-3,n-2\} \end{Bmatrix} \]

2. 轨道-稳定子群定理

我们之前的环即为轨道，对于一个染色 \(c\) 我们定义其轨道为 \(G\cdot c = \{g\cdot c|g\in G\}\)

我们考虑，对于所有把 \(c\) 映射到自己的元素组成的集合 \(G_c = \{g \in G,g \cdot c = c\}\)，容易发现
\((G_c, ·)\) 也构成一个群，我们称其为 \(c\) 在 \(G\) 中的 \(\lceil\)稳定子群(Stable subgroup)\(\rfloor\)，有
时也称作 \(\lceil\)稳定子\(\rfloor\)。