组合基础
一、基础原理
1.加法原理
2.乘法原理
3.排列
集合大小为n,从无序到有序\(\times n!\)
多重排列
\[\frac{(x_1+x_2+x_3+…+x_m)!}{x_1!x_2!…x_n!}
\]
二重排列 \(0/1\) 两个集合,即组合数
\[\frac{n!}{m!(n-m)!} = C_n^m=\binom n m
\]
注:\(\binom n m\)为组合数的另一种记法,为使下面的blog更加清晰,
二、一堆定理/结论
T1
\[\binom n m = \binom n {n-m}
\]
T2
\[\binom n m = \frac n m \binom {n-1}{m-1}
\]
T3 杨辉三角
\[\binom n m = \binom{n-1} m + \binom {n - 1}{m - 1}
\]
1.组合意义证明:
\(\binom n m\)表示在\(n\)个点中选出\(m\)个数,等价于\(\begin{cases}选第1个数,再在剩下的里面选(m-1)个数&\binom {n-1} {m-1} \\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~加上&~~~+\\ 不选第1个数,再在剩下的里面选m个数&\binom {n-1} m\end{cases}\)
2.代数证明:
\[\binom{n-1} m + \binom {n - 1}{m - 1}
\]
\[\Downarrow
\]
\[\frac{n-m}{n-m}\binom{n-1}{m} + \frac m m\binom{n-1}{m-1}
\]
\[\Downarrow
\]
\[\frac{(n-1)!\times(n-m)}{m!\times (n-1-m)!\times (n-m)} + \frac{(n-1)!\times m}{(n-m)!\times (m-1)!\times m}
\]
\[\Downarrow
\]
\[\frac{(n-1)!\times(n-m)}{m!\times(n-m)!}+\frac{(n-1)!\times m}{(n-m)!\times m!}
\]
\[\Downarrow
\]
\[\binom n m
\]
T4 二项式定理
\[(a+b)^n = \binom n 0 a^0b^n+\binom n 1 a^1 b^{n-1} + …+\binom n n a^nb^0 = \sum_{i = 0}^n \binom n i a^ib^{n-i}
\]
1.组合意义证明
将\(a、b\)看成两个集合即可
2.生成函数证明\(e^{an}* e^{bn}\)(注:*为卷积)
由生成函数知:(不会,喵)
3.泰勒展开-广义二项式定理(不会了,咕咕咕)
T5
\[\sum_{i=0}^n\binom n i = 2^n
\]
1.组合意义证明
在两个集合里边取\(n\)个数一共有\(2^n\)种,等于在其中一个集合中选\(\{0,1,2,3,…,n\}\)个数的方案和
2.卷积证明
\[\{1,1\}卷n次\to\{\binom n 0,\binom n 1,\binom n 2,…,\binom n n\}
\]
T6
\[\binom n r\binom r k = \binom n k\binom {n-k}{r-k}
\]
1.组合意义证明
我们先画一个图
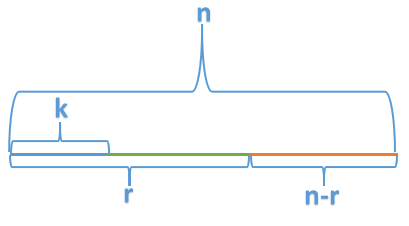
先在\(n\)个里面选\(r\)(绿+蓝)个,再在\(r\)个里面选\(k\)个(蓝) \(\binom n r\binom r k\)
先在\(n\)个里面选\(n-k\)个(绿+蓝)个,再在\(n-k\)个里面选\(r-k\)个(绿) \(\binom n r \binom {n-k}{r-k}\)
这两种方法都可以吧这一个线段分成三种颜色,可以证明他们是一样的
2.打开公式
\[\frac {n!}{r!\times (n-r)!}\times \frac {r!}{k!\times (r-k)!} = \frac{n!}{(n-r)!(r-k)!}
\]
T7 范德蒙卷积
对于任意给定的\(n,t,m\)有:
\[\sum_{i=0}^t\binom{n}{i}\binom{m}{t-i} = \binom{n+m}{t}
\]
-
组合意义证明:
考虑在n中选了i个数,m中选剩下的
-
二项式定理\((1+x)^{n+m} = (1+x)^n(1+x)^m\)
T8
\[\sum_{i=0}^n \binom{n}{i}^2
\]
利用\(T1\),\(T7\)的性质
\[\sum_{i=0}^n\binom{n}{i}\binom{n}{n-i}
\]
\[\binom{2n}{n}
\]
T9 Lucas定理
\[\binom n m = \binom {\lfloor \frac n k \rfloor}{\lfloor \frac m k\rfloor}\binom {n\%k}{m\% k}
\]
证明:
我们要求下面一个式子的值\(0\leq t,r <p\):
\[\binom {sp+t}{kp+r}\mod p
\]
即\([x^{kp+r}](1+x)^{sp+t}\mod p\)(此处含有生成函数的取项操作,不会看blog)
\[(1+x)^{sp+t} \equiv {((1+x)^p)}^s\times (1+x)^t\mod p
\]
又因为:
\[(1+x)^p \equiv 1 + \binom p 1x+\binom p2x^2+…+\binom p px^p\equiv1+x^p\mod p
\]
所以:
\[(1+x)^{sp+t} \equiv (1+x^p)^s\times(1+x)^t\equiv\sum_{i=0}^s\binom si x^{ip} ~\times ~\sum_{j=0}^t\binom tjx^j\mod p
\]
\[(1+x)^{sp+t}\equiv \sum_{i=0}^s\binom s i\sum _{j=0}^t\binom tj x^{ip+j}\mod p
\]
若要取\(x^{kp+r}\)的常数,\(i = k\),\(j = r\)
\[[x^{kp+r}](1+x)^{sp+t}\equiv \binom sk\times \binom tr\equiv\binom {\lfloor \frac n k \rfloor}{\lfloor \frac m k\rfloor}\binom {n\%k}{m\% k}\mod p
\]
得证
T10
\[\sum_{i = k}^{n}\binom i k = \binom{n+1}{k+1}
\]
1.杨辉三角证明:
考虑把第\(k\)行、第\(k\)列的数挪到第\(k+1\)行、第\(k+1\)列即可向下推(因为两个数相等,都为\(1\))
2.证明:
\[\binom {k+1}k = 0
\]
\[\Downarrow
\]
\[\sum_{i = k}^n\binom i k = \binom {k}{k+1} + \binom k k+\binom {k+1}k+…+\binom n k
\]
\[\Downarrow
\]
\[\sum_{i = k}^n\binom i k =\binom{k+1}{k+1} +\binom{k+1}k+…+\binom n k
\]
\[\vdots
\]
\[\sum_{i = k}^n\binom i k =\binom {n+1}{k+1}
\]
T11
\[\sum_{i=0}^ni\times \binom n i = n \times 2^{n-1}
\]
- 代数法证明:(感谢jeffy给予的帮助)
\[原式=0\binom n 0 + 1\binom n 1 + 2\binom n 2 + …+n \binom n n
\]
\[=\frac 1 2\sum_{i = 0}^n n \times \binom n i
\]
\[= \frac{n}{2}\sum_{i= 0}^n \binom n i
\]
\[= \frac n 2\times 2^n
\]
\[= n\times 2^{n-1}
\]
2.生成函数证明(不了解生成函数的可以看我的另一篇blog)
左边是序列,右边是对应的生成函数
由生成函数可以知道:
\[<\binom n 0,\binom n 1,\binom n 2,…>\Longrightarrow(1+x)^n
\]
考虑我们先进行求导
\[<\binom n 1,2\binom n 2,\binom n 3,…>\Longrightarrow[(1+x)^n]' = n(1+x)^{n-1}
\]
再进行右移1位
\[<0,\binom n 1,2\binom n2,3\binom n 3,…>\Longrightarrow nx(1+x)^{n-1}
\]
从而得到了我们的目标序列
\[<0,\binom n 1,2\binom n 2,3\binom n 3,…>
\]
那如何对这一个序列求和呢?
很简单,只需要让生成函数的\(x = 1\)即可
\[\sum_{i=0}^{n}i\times \binom n i = n\times 1\times(1+1)^{n-1} = n\times 2^{n-1}
\]



