二分图匹配

一、前置芝士

• 图论
• 二分图（下面会讲）

二、二分图

定义

设\(G=(V,E)\)是一个无向图，如果顶点\(V\)可分割为两个互不相交的子集\((A,B)\)，并且图中的每条边\((i,j)\)所关联的两个顶点\(i\)和\(j\)分别属于这两个不同的顶点集，则称图\(G\)为一个二分图。学过高中数学的
话应该能看懂我在说什么逃

更简单的定义

顶点集\(V\)可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。满足这样的图就叫二分图。

还是看不懂？？？来一张图

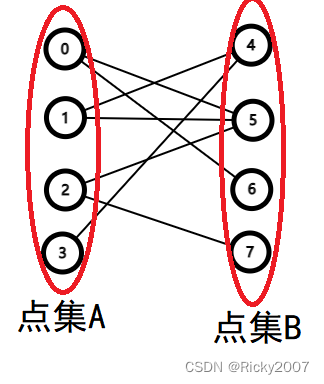
图中有两个点集，点集A、B相互连边，内部不连边的图即为二分图。

二分图的判定

考虑黑白染色 （不懂的可以问度娘），如果能染色即为二分图

三、二分图匹配

匈牙利算法

本质：反悔贪心
枚举子集A中还没有匹配的点，设此点为\(u_i\)，将它连向的点设为\(v_i\)，看 是否已经和某一个\(u_j\)匹配。

• 若不是，则：直接将\(u_i\)和\(v_i\)匹配。
• 若是，则：尝试能否更换\(v_i\)的匹配点为\(u_i\)
  \(u_j\)此时失去了匹配点，尝试重新为\(u_j\)寻找一个匹配点
  重复执行上述算法流程直到当前需要匹配的点找到了匹配点或者当前\(s_i\)连向的所有点都已经被更换过匹配。
  注意：我们不会为已经更换过匹配点的\(t_i\)重新更换匹配。

上述算法实际上是对于每一个A中的点贪心地去找它能否匹配，每次处理一个点总匹配对数要么不变要么加1，在最大匹配中的点一定会被匹配。

复杂度：

枚举每一个点，每次都有可能遍历全图，复杂度为\(O(n * V)\)

正确性：考虑可以自己尝试进行证明 口糊

更优秀的算法？

用dinic跑最大流的复杂度只有\(O(v * \sqrt V)\)
匈牙利能过谁写网络流啊

---

四、一些例题以及代码

P3386 【模板】二分图最大匹配

#include<cstdio>
using namespace std;
const int NN = 5e4+8;
int n,m,e,tag,ans;
int p[NN],vis[NN];//p为配对的数，vis为标记

struct Edge{
	int next,to;
}edge[NN];
int head[NN],cnt;
void init(){
	for(int i = 0; i <= n; i++)head[i] = -1;
	cnt = 0;
}
void add_edge(int u,int v){
	edge[++cnt] = {head[u],v};
	head[u] = cnt;
}//链式前向星

bool match(int x){
	for(int i = head[x]; i != -1; i = edge[i].next){
		int tt = edge[i].to;
		if(vis[tt] == tag)continue;
		vis[tt] = tag;//打标记
		if(p[tt] == 0){
			p[tt] = x;
			ans++;//最大匹配数
			return true;
		}
		else if(match(p[tt])){
			p[tt] = x;
			return true;
		}
	}
	return false;
}//匈牙利算法

int main(){
	scanf("%d%d%d",&n,&m,&e);
	init();
	for(int i = 1,u,v; i <= e; i++){
		scanf("%d%d",&u,&v);
		add_edge(u,v);
	}
	for(int i = 1; i <= n; i++){
		tag = i;match(i);//连边
	} 
	printf("%d",ans);
} 

P4251 [SCOI2015]小凸玩矩阵

• Step 1：求第k大的数的最小值，直接考虑二分答案
• Step 2：因为每一行和每一列的不能重复，可以考虑二分图匹配
• Step 3：因为求最小，所以可以建小于等于二分值的边（当然也有其他方法）

#include<cstdio>
#include<cstring>
using namespace std;
const int NN = 300;
int n,m,tag,res,k;
int A[NN][NN],pair[NN],flag[NN];//A为所给矩阵，pair为v[i]的配对，flag为标记
bool match(int u,const int & lim){
	for(int v = 1; v <= m; ++v){
		if(A[u][v] > lim) continue;//考虑省略建边
		if(flag[v] == tag) continue;
		flag[v] = tag;
		if(pair[v] == 0){
			pair[v] = u;++res;return true;
		}
		else if(match(pair[v],lim)){
			pair[v] = u;return true;
		}
	}
	return false;
}//匈牙利
bool erf(int &lim){
	memset(pair,0,sizeof(pair));
	memset(flag,0,sizeof(flag));
	res = 0;
	for(int i = 1; i <= n; ++i)
		tag = i,match(i,lim);
	if(res < k) return true;
	else return false;
}//二分判断条件
int main(){
	scanf("%d%d%d",&n,&m,&k);
	k = n-k+1;
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j <= m; ++j){
			scanf("%d",&A[i][j]);
		}
	}//输入矩阵
	int l = 0,r = 1e9+7,mid,ans = 0;
	while(l <= r) {
		mid = (l + r) / 2;
		if(erf(mid)){
			l = mid +1;
		}
		else{
			r = mid - 1;
			ans = mid;
		}
	}//二分
	printf("%d",ans);
} 

彩蛋：如何求出二分图中，使得匹配数为最大匹配的匹配的数量

---

写出文章实属不易，求点赞、收藏、关注，谢谢！

---