算法中的复杂度分析
复杂度
前言
来复习下，算法体重经常聊到的复杂度
算法中我们经常会从两个角度去考虑算法的优劣，那就是【时间维度】和【空间维度】
时间复杂度
时间复杂度：就是执行当前算法消耗的时间。
当然我们这里讲的时间复杂度是个更加通用的描述，因为我们知道代码在不同中机器中执行的时间是不同的，性能好的机器可能就用的时间更短。
所以我们这里的时间复杂度，用的是【大O符号表示法】，即T(n) = O(f(n))
如何理解呢？先来个栗子
func sum(n int) int {
sum :=0
i:=3
for m:=0;m<n;m++ {
sum+=n*i+1
}
return sum
}
比如上面这段代码，循环了n次，那么时间复杂度就是O(n)，如何分析呢？
我们假定每行代码执行的时间是一个时间颗粒，那我们上面的例子，第2和3行一共两个时间颗粒，4和5行就是2*n个时间颗粒，总共就是(2n+2)个时间颗粒。
当然这样算下来时间复杂度是T(n) = O(2n+2)，大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。
如果 n 很大时，而公式中的低阶、常量、系数三部分并不左右增长趋势，所以都可以忽略。也就是2n中的2和常量2都可以忽略，所以时间复杂度就是T(n) = O(n)
常数阶O(1)
无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)，如：
func sum(n int) int {
sum :=0
i:=3
sum=sum*i
return sum
}
因为这段代码中没有一个系数，会导致代码的执行时间随系数的变化而变化，所以不管这个代码有多少行，都可以时间复杂度是 O(1)
一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。
线性阶O(n)
比如我们刚开始的这个例子
func sum(n int) int {
sum :=0
i:=3
for m:=0;m<n;m++ {
sum+=n*i+1
}
return sum
}
代码中有个 for 循环，代码的执行时间会因为 n 的变化而变化，并且是线性增加或减少，所以这里用 O(n) 来表示他的时间复杂度。
对数阶O(logN)
func sum(n int) int {
sum :=0
for sum<n {
sum+=n*2
}
return sum
}
这里同样也是一个循环，只不过每次都乘以2。也就是2的 x 次方大于等于 n 。 执行的次数就是 x 。
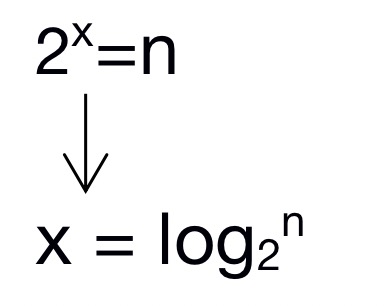
接着上面转换的结果，对于省略掉常数2，所以时间复杂度就是 O(logN)
实际上，不管是以2为底、以3为底，还是以10为底，我们可以把所有对数阶的时间复杂度都记为 O(logn)
线性对数阶O(nlogN)
将上面的代码实例，外面在循环 n 次，时间复杂度就是下面我们要讨论的 O(nlogN)
func sum(n int) int {
sum :=0
for i:=0;i<n;i++{
for sum<n {
sum+=n*2
}
}
return sum
}
这个就不展开讨论了，内层循环是上面我们讨论的 O(logN) ，外面多了一层循环，所以时间复杂度就是 O(nlogN)
平方阶O(n²)
这个就很好理解了，就是两层代码的循环
func sum(m,n int) int {
sum :=0
for i:=0;i<m;i++{
for j:=0;j<n;j++ {
sum+=j
}
}
return sum
}
当然有三层循环就是 O(n³)，依次类推
空间复杂度
空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。
来个栗子分析下
func test(n int) map[int]struct{} {
testMap := make(map[int]struct{}, n)
for i := 0; i < n; i++ {
testMap[i] = struct{}{}
}
return testMap
}
比如上面的这段代码，空间复杂度是 O(n)
我们可以看到 for 开始的时候申请了一个变量 i ，这是常量级别的，跟数据规模 n 没有关系，所以我们可以忽略。我们初始化了一个长度为 n 的 testMap。testMap 的长度会根据 n 的变化而变化，所以这段代码的空间复杂度就是 O(n)。
常数阶O(1)
这个很简单
func sum(n int) int {
sum :=0
i:=3
sum=sum*i
return sum
}
因为没有变量跟随数据规模 n 的变化而变化，所以空间复杂度就是 O(1)。
平方阶O(n²)
看个栗子
func test(n int) [][]int {
var sil = make([][]int, n)
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
sil[i] = append(sil[i], j)
}
}
return sil
}
定义了二维切片，随着两层循环，分别申请了 n*n 个空间的大小，所以空间复杂度就是 O(n²)
当然有二维切片就是 O(n³)，依次类推
最好、最坏情况时间复杂度
最好情况时间复杂度就是，在最理想的情况下，执行这段代码的时间复杂度。
最坏情况时间复杂度就是，在最糟糕的情况下，执行这段代码的时间复杂度。
比如这段代码
func sum(n, m int) int {
sum := 0
for i := 0; i < n; i++ {
if sum == m {
return sum
}
sum += i * 2
}
return sum
}
如果在第一次循环的时候，sum == m 就结束程序，那么这个时候的时间复杂度就是最好时间复杂度。
当然如果上面的 for 循环，遍历到最后一次也没满足 sum == m，那么这个时候的时间复杂度就是最坏情况时间复杂度。
平均情况复杂度
顾名思义就是，最好和最坏的时间复杂度的平均值。
比如上面的那个例子
引入概率之后，前面那段代码的加权平均值为(3n+1)/4。用大O表示法来表示，去掉系数和常量，这段代码的加权平均时间复杂度仍然是O(n)。
均摊时间复杂度
对一个数据结构进行一组连续操作中，大部分情况下时间复杂度都很低，只有个别情况下时间复杂度比较高，而且这些操作之间存在前后连贯的时序关系，这个时候，我们就可以将这一组操作放在一块儿分析，看是否能将较高时间复杂度那次操作的耗时，平摊到其他那些时间复杂度比较低的操作上。而且，在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。
其实也可以认为均摊时间复杂度就是一种特殊的平均时间复杂度。
总结
这里大概介绍了空间复杂度和时间复杂度
时间复杂度的全称是渐进时间复杂度，表示算法的执行时间与数据规模之间的增长关系。类比一下，空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。
这里的计算使用的是【大 O 复杂度表示法】，时间复杂度和空间复杂度只和数据规模 n 有关系，公式中的低阶、常量、系数三部分不影响增加趋势，所以不收这三个的影响。
参考
【算法的时间与空间复杂度（一看就懂）】https://zhuanlan.zhihu.com/p/50479555
【数据结构与算法之】https://time.geekbang.org/column/intro/100017301
【空间复杂度和时间复杂度】https://boilingfrog.github.io/2021/10/03/算法中的复杂度分析/
