【原创】寻找方程等于0的数值算法总结
机器学习中,很多问题都可以归结为寻找 f(x)=0 的点(例如,凸优化问题,寻找导数为0的点)。很多时候f(x)=0的解析解很难计算,下面,我们就总结一下该问题的数值计算方法。
1. Newton's Method(牛顿法)
牛顿法是利用函数在当前点的切线作为函数的近似,寻找当前点切线=0的点,作为下一个搜寻点。牛顿法的迭代公式如下:
\[{x_{n + 1}} = {x_n} - \frac{{f({x_n})}}{{f'({x_n})}}{\mkern 1mu} \]
下面是牛顿法法收敛的动态图示:
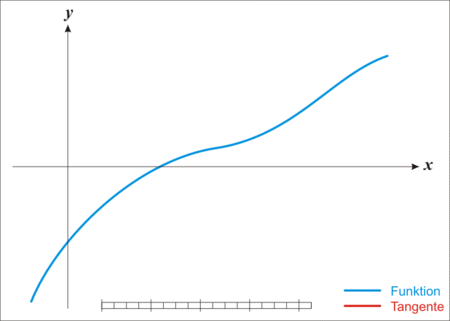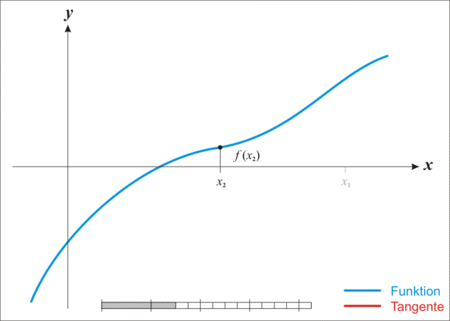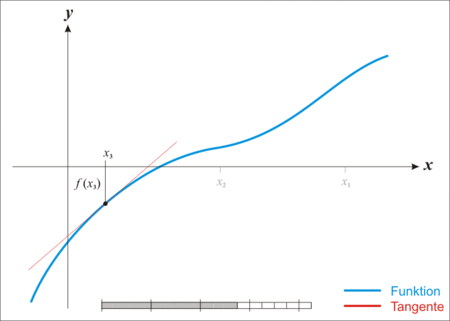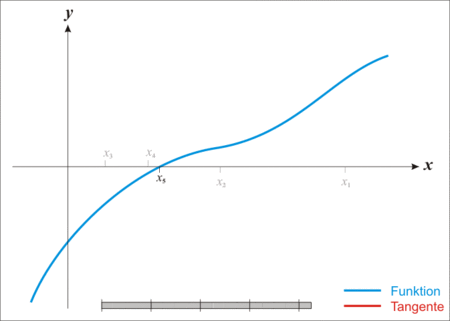
(注意:最优化问题里也有个”牛顿法“。虽然此”牛顿法"非彼“牛顿法”,但两者的思想还是挺相似的。最优化问题里,牛顿法是用二阶泰勒展开来近似当前的函数。)
2. Secand Method
该算法是牛顿法的近似,用上两个搜寻点的连线取代牛顿法里的切线,该线与y=0的交点就是下一个搜寻点。于牛顿法相比,Secand Method不需要计算导数,对于一阶不可微的函数,同样适用。算法的迭代公司如下:
\[{x_n} = {x_{n - 1}} - f({x_{n - 1}})\frac{{{x_{n - 1}} - {x_{n - 2}}}}{{f({x_{n - 1}}) - f({x_{n - 2}})}}\]
下面是Secand Method的迭代示意图:

3. Muller‘s Method
Muller's算法形式与Secand Method类似。不同的是Muller's算法通过本次迭代之前的三个迭代点信息来近似原函数。Muller算法与Secand算法的区别有点像最优化算法中梯度法和牛顿法的区别,前者都是一阶趋势迭代,后者都是二阶趋势迭代。Muller’s Method的迭代公式如下:
\[{y_k}(x) = f({x_{k - 1}}) + (x - {x_{k - 1}})f[{x_{k - 1}},{x_{k - 2}}] + (x - {x_{k - 1}})(x - {x_{k - 2}})f[{x_{k - 1}},{x_{k - 2}},{x_{k - 3}}]\]
其中,\(f[{x_{k - 1}},{x_{k - 2}}]\)和\(f[{x_{k - 1}},{x_{k - 2}},{x_{k - 3}}]\)是分差(Divided differences)。
\[f[{x_\nu }, \ldots ,{x_{\nu + j}}]: = \frac{{f[{x_{\nu + 1}}, \ldots ,{x_{\nu + j}}] - f[{x_\nu }, \ldots ,{x_{\nu + j - 1}}]}}{{{x_{\nu + j}} - {x_\nu }}}\]
4. Householder's method
Householder's method是一类通用算法,牛顿法只是Householder's method的一个特例。 Householder's method的迭代公式如下所示:
\[{x_{n + 1}} = {x_n} + d\;\frac{{{{\left( {1/f} \right)}^{(d - 1)}}({x_n})}}{{{{\left( {1/f} \right)}^{(d)}}({x_n})}}\]
可以证明:
\[|{x_{n + 1}} - a| \le K \cdot |{x_n} - a{|^{d + 1}}\]
所以,Householder's method算法的收敛速度是(d+1)阶。但是,有学者认为,算法的收敛更多的是来自迭代次数,而不是单次迭代的收敛速度。因此,2阶以上的收敛算法很少在实际中有应用。
当d=1是,该算法就与上文提到的牛顿算法等价,推到公式如下:
\[\begin{array}{*{20}{c}}
{{x_{n + 1}} = }&{{x_n} + 1{\mkern 1mu} \frac{{\left( {1/f} \right)({x_n})}}{{{{\left( {1/f} \right)}^{(1)}}({x_n})}}}\\
= &{{x_n} + \frac{1}{{f({x_n})}} \cdot {{\left( {\frac{{ - f'({x_n})}}{{f{{({x_n})}^2}}}} \right)}^{ - 1}}}\\
= &{{x_n} - \frac{{f({x_n})}}{{f'({x_n})}}}
\end{array}\]
参考文献:
1. http://en.wikipedia.org/wiki/Newton%27s_method
2. http://en.wikipedia.org/wiki/Secant_method
3. http://en.wikipedia.org/wiki/Muller%27s_method
4. http://en.wikipedia.org/wiki/Householder%27s_method




