老生常谈的直接插入排序、冒泡和选择排序

排序原理

有些排序算法，可以归纳为“有序区扩张，无序区收缩”。所谓有序区，就是在此区间的元素都已经是有顺序的了，无序区则是在此区间的元素都是杂乱无章的。接下来我们先看几个典型的“有序区扩张，无序区收缩”算法。

直接插入排序

首先，选定一端为有序区，然后将其余所有元素归入无序区，比如说有个待排序列是这样的：

[0, 1, 2, 3,  4,  5,  6, 7]  // 下标
[1, 5, 8, 10, 36, 24, 5, 9]  // 元素列表

首先，我们可以选定以下标 0 为有序区，其余所有元素 1 - 7 则都属于无序区，按照有序区扩张，无序区收缩的原则，每次从无序区中选定一个元素加入有序区中，对于直接插入排序来说，则顺序地从无序区中选择一个元素，然后放入有序区中，我们用 | 来分隔有序区和无序区，则刚开始时：

[1, | 5, 8, 10, 36, 24, 5, 9]

然后这样：

[1, 5, | 8, 10, 36, 24, 5, 9]

就这样直到无序区不再有元素：

[1, 5, 8, | 10, 36, 24, 5, 9]
[1, 5, 8, 10, | 36, 24, 5, 9]
[1, 5, 8, 10, 36, | 24, 5, 9]
[1, 5, 8, 10, 24, 36, | 5, 9]
[1, 5, 5, 8, 10, 24, 36, | 9]
[1, 5, 5, 8, 9, 10, 24, 36 |]    // 无序区不再有任何元素，结束

然后转化为核心代码就像这样：

// 参数表示从下标为 begin - end 的元素集合将被排序，下标从 0 开始，包括 begin 和 end
public static void insertSort(int[] data, int begin, int end) {

    // i 表示无序区第一个元素的下标，即等于在无序区中选中了一个元素，相当于无序区在收缩
    for (int i = begin + 1; i <= end; i++) {

        // 那么接下来就是要把这个从无序区中选中的元素放入有序区中，等同于有序区在扩张
        // 如果从无序区中选中的元素已经比有序区最后一个元素大了，也就是不用再找位置了，直接坐下就行！
        if(data[i] < data[i-1]) {

            // 用一个临时值代表这个选中的元素，从而避免需要频繁交换元素
            int tmp = data[i];

            // j 初始化为有序区最后一个元素下标
            int j = i - 1;

            // 怎么放呢？这里提供一种方式：
            // 从有序区逆序遍历，只要有序区中选中的元素不如无序区中选中的元素小，那么自动向前一步
            for (; j >= begin && data[j] > tmp; j--) {
                data[j + 1] = data[j];
            }

            // 经过有序区的大元素让步后，无序区中选中的元素就找到了自己的位置
            // 为什么是 j + 1 呢？因为下标为 j 的元素不满足向前一步的条件，所以是在它前面空了一个位置
            data[j + 1] = tmp;
        }
    }
}

冒泡排序

所谓冒泡排序，就是说像鱼吐泡泡一样，从无序区的第一个元素开始遍历直到无序区再无元素，每个元素都与前一个元素对比，这叫一趟冒泡，每趟都会产生一个元素进入有序区，当无序区再无元素时，待排数列已是有序。可能我说地太抽象了，来看下这张图：

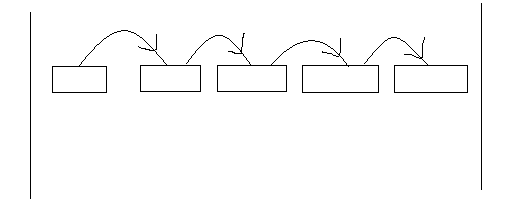
初始时，大家都在无序区，一趟冒泡后，变成了下面这样，有一个元素脱离了无序区，进入了有序区：

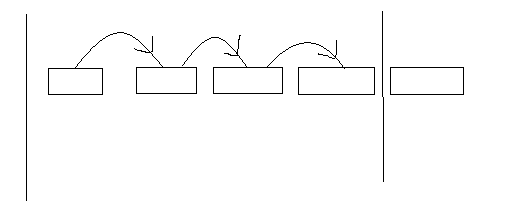
就是像这样，一个两个喵，你和我，心连心，手牵手... 咳咳，打个比方，有某桃园三结义某天排队去买奶茶，他们刚开始是这样排的(他们三个都属于无序区)：

| 小刘、小张、小关 |

突然大哥觉得自己应该在前面，也就是看上了二弟的位置，于是对三弟说，三弟，站大哥后面来！小张一听，大哥这是想插队啊，但秉着尊老爱幼的美德还是站到了大哥后面，然后就变成了这样：

| 小张、小刘、小关 |

大哥再看，二弟还在前面，不行，再来，于是就变成了这样，大哥成功占领二弟的位置：

| 小张、小关、| 小刘

这里，小刘的这种做法就是典型的一趟冒泡，最终小刘进入了有序区，只留下二弟和三弟在无序区中凌乱

转化为核心代码就像这样：

// 参数表示从下标为 begin - end 的元素集合将被排序，下标从 0 开始，包括 begin 和 end
public static void bubbleSort(int[] data, int begin, int end) {

    // i 表示从无序区中的选出来的元素将要放到有序区中的位置
    for (int i = end; i > begin; i--) {

        // 如果一轮冒泡中元素之间未发生过任何位置交换，那么这序列已是有序的了
        boolean changed = false;

        // 有序区的位置已经确定了，那么接下来就是从无序区中确定谁将坐上那个位置！
        // 怎么确定呢？打一架就行，谁赢谁上，赢者继续打，直到产生一个最终赢家，无疑它就是全场最厉害的
        for (int j = begin; j < i; j++) {

            // 如果打赢了就能够往前一步，继续下一场比赛
            if (data[j] > data[j + 1]) {
                swap(data, j, j + 1);

                // 元素位置发生了交换
                changed = true;
            }
        }

        // 如果没有元素交换过位置，已是有序，结束
        if (!changed) return;
    }
}

选择排序

有了冒泡排序的基础，难道还要慌这个吗？前面说过，冒泡排序是先确定了从无序区中选中的某个元素在有序区的位置，然后开始从无序区中选择一个元素放入这个位置。在冒泡排序中使用的是一个两个喵，啊呸，是擂台赛打架的方式确定最强者，打赢的就往前走，赢者的赢者的赢者...就是走在时代前列的人！但这样打一下走一下实在太费时间了，大家原地打就好了，如果我是最强者，我直接坐上有序区的宝座，就不用走那么多弯路了。

那么，既然这样，代码就变成这个风格了：

public static void selectSort(int[] data, int begin, int end){

    // i 表示本轮有序区的唯一位置，依次扩张
    for (int i = end; i > begin; i--) {
        
        // 假设现在坐在有序区唯一宝座上的是最强者
        int max = i;

        // 底层人物个个不服这最强者，纷纷欲与之一较高下
        for (int j = begin; j < i; j++) {
            
            // 打赢的
            if (data[j] > data[max]){
                // 最强者称号就是你的，但还不能坐上宝座，还得接受别人的挑战，直到大家都打不过你
                max = j;
            }
        }

        // 都打服之后，如果发现最强者不是原来坐在宝座上的人，那么不好意思，你来我的位置，我带着我的荣耀登上这宝座
        if (max != i){
            swap(data, i, max);
        }
    }
}