《Introduction to Algorithm》-chaper30-多项式与快速傅里叶变换

 

  两个n次多项式的相加最直接的方法所需要的时间是O(n)，而实现两个n次多项式的乘法的直接方法则需要O(n^2)，本章讨论的快速傅里叶变换(FFT),将会将这一过程的时间复杂度降至O(nlogn).同时本章也会给出一些FFT现实应用.

                         

  多项式的两种表示形式：

 

 

 

    通过上面的推导，我们简单总结一下得到的结论。

 

 

 

 

  而接下来问题的核心是，如果优化求值和插值过程的时间复杂度，求值过程直观的来看，时间复杂度是O(n^2)，而插值过程需要解线性方程组，需要的时间复杂度更高。

  为了算法的优化，我们需要引入一些复变函数的知识.

 

  下面这个是以n=8为例做出的草图。

 

  容易看到对于一个周期内，k=0,1,2,…,7分别有8个不等的复数解.

 

 

   以上详细给出了复变函数中的一些知识，需要尤为注意折半引理，这个引理是后面优化算法的核心，也是设计递归算法的核心所在。

     

    

   

   4,5行定义了主n次单位根和第一个根，这是为了在后面得到n个n次单位复数根.

   8,9行是基于折半引理的递归过程。

   10,11,12,13是根据递归“回归”的部分，即根据分治的结果得到母问题的解。13行的设置，结合循环，完成更新w的值的任务。

  

   简单的考察FFT的时间复杂度，有如下等式：

  T(n)=2T(n/2)+O(n)=O(nlgn)

 

 

  以上我们完成了对次数界为n的多项式的快速求值，即多项式的系数表达到多项式的点值表达。下面则开始讨论对次数界为n的多项式在n个点处的快速插值，即多项式的点值表达到多项式的系数表达。这个过程我们也称其为逆DFT。

 

 

 

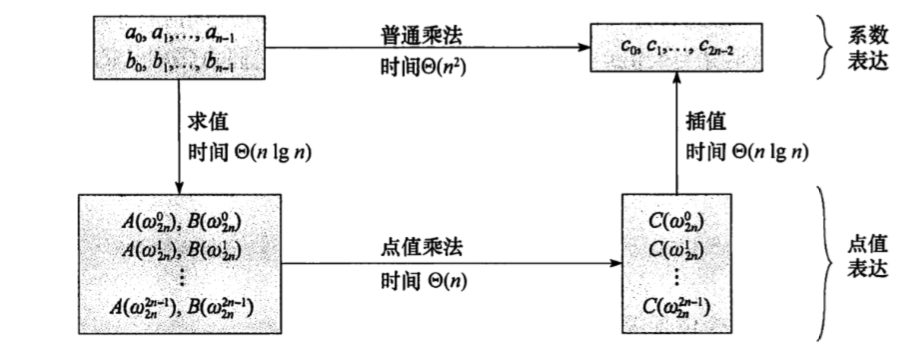
  那么我们给出下图，便可以基于上述理论加速两个n次多项式的乘法了(O(nlgn))。