《A First Course in Probability》-chape4-离散型随机变量-几种典型分布列
超几何分布:
超几何分布基于这样一个模型,一个坛子中有N个球,其中m个白球,N-m个黑球,从中随机取n(不放回),令X表示取出来的白球数,那么:

我们称随机变量X满足参数为(n,m,M)的超几何分布。
考察其期望的求法:

几何分布:
在独立重复实验当中,每一次实验成功的概率是p,我们关注使得实验成功一次所需要重复的实验次数n及其对应的概率,很容易看到,我们有如下的分布列:

验证其作为分布列的性质:

几何分布的期望:
根据期望的定义,并在这里设q = 1-p

二项分布:
基于最基础的一个离散型随机变量——伯努利随机变量X,我们进行n次重复的实验,其概率分布结果就是所谓的二项分布。
具体点来说,就是某个实验成功的概率是p,现在我们进行n此时杨,设随机变量X表示n次实验后成功的次数,那么有如下分布列成立。

关于其期望,推导过程和几何分布、超几何分布中期望的推导是同质的,先推出X^k的表达式,然后根据二项式恒等关系,寻求自相似性建立递推关系,然后得到最终的期望值、方差。


关于二项分布概率值的单调性这里有这样一个命题:对于满足参数为(n,p)的二项随机变量,k取得[0,n]时,P{X=k}先递增,后递减,当k = (n+1)p时取得最大值。

基于我们最为熟悉的离散型分布——二项分布,我们能够衍生出很多别的分布列,对于之前介绍过的几何分布,我们赋予其的含义是:某个事件成功的概率是p,在n次独立重复实验中恰好成功一次的概率是多少。顺着这层含义,我们把1次编程r次,便得到了所谓的负二项分布。设负二项分布的随机变量是X,独立事件成功的概率是p,则在n次重复独立实验中恰好成功r次的概率是:

较之二项分布,我们能够看到,负二项分布更加强调n次重复实验中“恰好”成功r次,也就是要求第n次实验恰好是第r次成功的实验。
我们通过一个问题来进行举例——巴拿赫火柴问题。
Q:某个抽烟的数学家总是随身带着两盒火柴,一盒放在左边口袋一盒放在右边口袋。每次他需要火柴时,他就从任意的口袋中的火柴盒中取出一个火柴,现在两盒火柴中都各有N个火柴,那么请问他第一次发现其中一个盒子已经空了的时候,另一盒恰好有k根火柴的概率有多大?
分析:首先我们需要讨论的一个点是,这个火柴位于哪个口袋的火柴盒是空的,显然是左是右具有对称性,我们分析一种情况,进行平方即可。
假设左口袋为空,那么这个过程的最后一个步骤显然是在数学家第2N-k次取火柴的时候,必然取走了右口袋中的一根火柴,这是一位他拿走左口袋的最后一根火柴的时候,我们就可以默认理性的数学家不会再去拿左口袋的火柴盒,因此我们就可以将其与负二项分布联系起来:在2N-k次重复实验当中,恰好有N次从左口袋取出的概率。
即

当然,这道问题的最终结果是将这个概率平方。
负二项分布的期望:
直接推导是难以给出E[X]有关负二项分布的参数r、p的联系的,因此这里我们考虑建立递推关系。
结合之前复合随机变量的计算法则,我们在这里容易得到如下的等式。

从二项分布结合级数推导而来的泊松分布:
对于二项分布我们很熟悉,在生活当中我们也很常用,但是其计算公式不免显得有点繁琐,我们现进行如下的简化推导:
设某个二项分布的参数是(n,p),设置参数λ=np.随机变量为X.

同时结合几种极限求法,我们能够看到,当n趋近于无穷的时候,有:

因此我们得到:

这便是泊松分布列。容易看到,n趋近于无穷的二项分布可以与泊松分布等价,如果基于n趋近于无穷,我们可以验证泊松分布的作为分布列的一个性质:

泊松分布的数字特征:
下面讨论泊松分布的期望和方差。
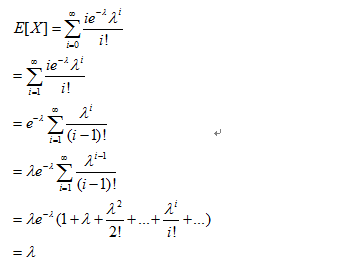

Ps:推导过程用到了泰勒级数的展开式,具体的内容笔者在《托马斯大学微积分》的专栏中会给出。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号