组合数学及其应用——卡特兰数

  卡特兰数是组合数学中常见也是重要的特殊计数公式。

  首先给出一个现实问题的模型：

  给出凸多边形的边数n，求解该凸多边形内部不相交的对角线把这个区域分成三角形区域的方法数。

 

  首先我们进行初步的分析，当n=2，h2=1,也就是说对于三角形，划分的情况数是1.这似乎有些不好理解，由于三角形内部无法添加对角线，所以符合情况的就是三角形本身，情况数为1.

 

  下面我们讨论n取任意值的情况。

  看下面的图。

 

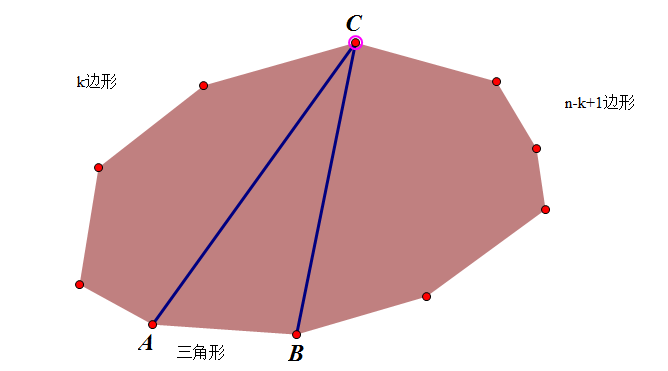
  考虑将n+1凸边形的子问题，即我们将AB视为基边，枚举C的位置，有n-1个可枚举位置，然后结合基本的计数原理，我们能够看到下面的递推式能够不重不漏的表示出h[n].

 

   

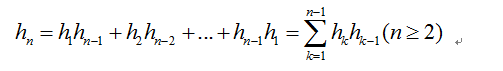
  而现在的问题在于，这样的递推公式是我们不喜爱的，我们喜欢的形式是斐波那契数列，给出的是前后项的关系式然后我们可以在线性时间复杂度下求出该数列，那么下面我们需要讨论的便是如何得到这个递推公式的解。

 

 

 

  下面是根据这条结论计算卡特兰数列的JAVA代码：

 

import java.io.*;
import java.util.*;
import java.math.BigInteger;


public class Main
{
 public static void main(String args[])
 {  
  BigInteger[] a = new BigInteger[101];
  a[0] = BigInteger.ZERO;
  a[1] = BigInteger.valueOf(1);
  for(int i = 2; i <= 100; ++i)
   a[i] = a[i - 1].multiply(BigInteger.valueOf(4 * i - 2)).divide(BigInteger.valueOf(i+1));
   Scanner in = new Scanner(System.in);
   int n;
   while(in.hasNext())
   {
    n = in.nextInt();
    System.out.println(a[n]);
   }
 }
}

  

 

 在引入卡特兰数列的实例模型中，我们从h1开始计数，考虑一般计数数列的使用习惯(从h0)开始，这里我们重新给出卡特兰数的定义：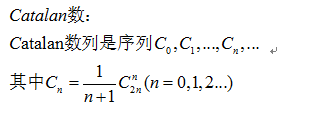

 

 

  这个定理将一系列的计数问题与卡特兰数联系了起来，而其中的关键就是部分和满足的那个大于等于0的不等式，下面呈现这个定理的证明，随后将会讨论一系列与之有关的实际问题。

 

   

 

  下面我们就来看几个通过这个定理联系在一起的实例。

   Ex1:2n个人排成一列进入剧场。入场券是50美分，2n个人中n个人手中有50美分，m个人手中有一元的纸币。剧场售票处的机械用一个空的收音机开始售票。有多少中排队方法能够成功的销售2n张票？

 

  分析：先简单化的考虑，将每个人视为相同的元素。将这个实际问题与刚刚给出的定理联系，题目的一个最大限制是，这个序列每当出现1美元的时候，售票处必须有大于一张的50美分。若我们将排队序列中50美分记为+1,1元纸币记作-1，那么对于我们排出的能够成功售出2n张票的序列，必须满足这个序列1~k这一段的和大于等于0(k∈[1,2n])，这就和定理内容联系了起来。再基于计数结果，将拿50美分的n个人视为不同元素，需要对n进行全排列。对拿1美元的人也是这样处理。

 

 

   Ex2：考虑在这样一个n x n的方格纸上，你当前的位置是(0,0),现在你的目标是(n,n),每一步中你可以选择上、下、左、右中任意一个方向前进一个单位长度，那么在所有从(0,0)到(n,n)的路线中，要求每一条路线中不能够穿越这个方格纸的对角线，那么请问有多少条符合要求的路线？

  注：所有路线均在2n步完成。

  分析：题目要求不能够穿过对角线，那么我们恰好将对角线当做对称轴，考虑上半部分可行的路线，根据对称性将最终的结果乘2即可。考察这样一个“上三角”区域，容易看到整条路线其实是n个+1和n个-1组成的序列，而所谓的+1、-1在这个问题中的具体含义便是：+1代表向上走一个单位长度，-1代表向右走一个单位长度。由于“不能越过对角线”这条限制，能够看到这个序列必须满足任意前k项和大于等于0的要求，这就又和上文我们给出的定理呼应起来，即我们可以得到结论，上三角区域的路线数是第n+1卡特兰数Cn

  即对于n x n的方格，总路线为2Cn.

 

  Ex3：当前有n个元素，我们需要将它们分别压入栈中然后全部取出，那么请问有多少中压栈(出栈)方案？

  分析：其实这个问题能够更加典型的诠释上文给出的定理。这里压栈操作我们视为+1，出栈操作视为-1，那么很显然能够完成n个元素均压入栈中并取出的条件是在2n个操作形成的+1、-1序列中，对于任意k，前k项要大于等于0，其结果是第n+1个卡特兰数Cn

 

 

  拟Catalan数：

                           

  

   

   分析：首先我们需要注意的一个问题是，在构造乘法方案的过程中，a x b和b x a是两种不同的方案，虽然在很多运算中是满足乘法交换律的，但对于矩阵乘法便不符合，虽然这里我们不讨论运算的结果。清楚这一点，将有利于理解后面的分析过程。