计算几何讲义——一道题目呈现的计算几何知识点

 

我们通过一个具体的题目来学习几个计算几何的知识点。

在计算几何中所谓的知识点，其实就是一个又一个的函数，因此在学习过程中要注意积累这些函数，并且要充分理解它们的使用条件，这样在用的时候才能够得心应手。

 Ex1：

  Morley定理告诉我们，任意三角形的三个角的6条三等分线会交出一个等边三角形记作△DEF，那么现在给出△ABC的三个顶点，请计算D、E、F的坐标.

                         

 

 分析：既然这道题目给出了原理，那么它的难点就主要在于如何取编程实现计算。我们首先来看一下为了求解这三个顶点，我们需要做一些什么，然后各自独立的分析，形成功能独立的函数。

 首先，求解三个顶点的过程中是存在对称性，因此我们找到求出一个顶点的方法即可，根据Morley定理，我们需要找到两个角的各自三等分线(靠近公共边的),他们的交点就是正三角形中的一个顶点。

 (1):两条三等分怎么找？

  考察这里我们有的已知条件：初始向量BC，旋转角度，旋转方向。然后现在我们想要求解旋转后的向量BD，因此这里我们用到向量旋转公式：

   

 

 

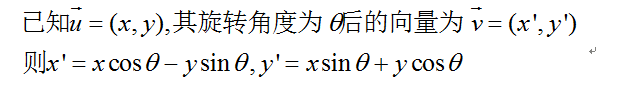
  (2)旋转角度怎么求？

  已知两个向量，求其夹角，用简单的点积就可以实现。

 

  (3)求得两条三等分直线后，如何求交点呢？

  需要注意的是，上文求得的所谓的“三等分直线”本质上是向量，而向量是可以平移的，因此我们需要用直线上边的点来限制向量的平移，也就是说，这里我们用向量参数来表示一条直线。

   

  看t1、t2的形式是不是很像克莱姆法则啊，猜对了，其实它就是一个线性方程组的解。

   

  完成了这些准备工作，关于代码实现，也就一目了然了。

  简单的参考代码如下：

  

#include<cstdio>
#include<cstring>
#include<cmath>

using namespace std;
struct point
{
    double x , y;
    point(double x = 0 , double y = 0):x(x),y(y){};//定义点的时候直接利用构造函数，很方便
};
typedef point Vector;//这里因为向量都有两个维度的有序参量

Vector operator + (Vector A,Vector B){return Vector(A.x+B.x , A.y+B.y);}
Vector operator - (point A,point B)  {return Vector(A.x-B.x , A.y-B.y);}
Vector operator * (Vector A,double p){return Vector(A.x*p , A.y*p);}
Vector operator / (Vector A,double p){return Vector(A.x/p , A.y/p);}

double Cross(Vector A , Vector B)//向量叉积
{
    return A.x * B.y - A.y * B.x;
}

point GetLineIntersection(point P ,Vector v , point Q , Vector w) //两直线交点(参数法)
{
    Vector u = P-Q;
    double t = Cross(w , u) / Cross(v ,w);
    return P+v*t;
}

Vector Rotate(Vector A , double rad)//向量旋转(逆时针是正角)
{
    return Vector(A.x*cos(rad) - A.y*sin(rad) , A.x*sin(rad) + A.y*cos(rad));
}

double Dot(Vector A, Vector B){return A.x*B.x + A.y*B.y;}//向量点乘
double Length(Vector A){return sqrt(Dot(A,A));}          //向量模长
double Angle(Vector A, Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}//向量之间夹角

point getD(point A , point B , point C)
{
    Vector v1 = C - B;
    double a1 = Angle(A-B , v1);
    v1 = Rotate(v1 , a1/3);

    Vector v2 = B - C;
    double a2 = Angle(A-C , v2);
    v2 = Rotate(v2 , -a2/3);
    return GetLineIntersection(B , v1 , C , v2);
}

int main()
{
    int T;
    point A,B,C,D,E,F;
    scanf("%d",&T);
    while(T--)
    {
      scanf("%lf%lf%lf%lf%lf%lf",&A.x,&A.y,&B.x,&B.y,&C.x,&C.y);
      D = getD(A,B,C);
      E = getD(B,C,A);
      F = getD(C,A,B);
      printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\n",D.x,D.y,E.x,E.y,F.x,F.y);
    }
    return 0;
}