数论习题
关于欧拉函数:
Q1(Problem source : poj 2478):
Description
F3 = {1/3, 1/2, 2/3} F4 = {1/4, 1/3, 1/2, 2/3, 3/4} F5 = {1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5}
You task is to calculate the number of terms in the Farey sequence Fn.
#include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> using namespace std; const int SIZE = 1000000 + 5; int phi[SIZE]; void init() { int i, j; memset(phi, 0, sizeof(phi)); phi[1] = 1; for(int i = 2; i < SIZE; i++) if(!phi[i]) { for(j = i; j < SIZE; j+=i) { if(!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i-1); } } } int main() { init(); int n; while(scanf("%d",&n)!=EOF && n) { long long sum = 0; for(int i = 2; i <= n; i++) { sum += phi[i]; } printf("%lld\n",sum); } }
for (variable = A; variable != B; variable += C) statement;I.e., a loop which starts by setting variable to value A and while variable is not equal to B, repeats statement followed by increasing the variable by C. We want to know how many times does the statement get executed for particular values of A, B and C, assuming that all arithmetics is calculated in a k-bit unsigned integer type (with values 0 <= x < 2k) modulo 2k.
考虑到这个层面,我们要做的本质上变成了求解同余方程:
A+Cx = B(mod 2^k)的最小非负整数解.
将其等价转化为Cx +2^k*y = B-A。
分别代入扩展欧几里得算法函数的参数即可求解.
简单的参考代码如下:
#include<cstdio> #include<iostream> using namespace std; void exgcd(long long a,long long b , long long &d , long long &x,long long &y) //gcd(a,b) = ax +by , d = gcd(a,b) { if(b==0) { x = 1;y =0; d = a ; return ; } else { exgcd(b,a%b,d,x,y); long long temp = x; x = y; y = temp - (a/b)*y; } } int main() { long long x ,y , m , n , l; long long a , b , c , d, k; while(cin >> a >> b >> c >> k &&(a + b + c + k)) { long long temp = c; c = b - a; a = temp; b = (long long)1 << k; exgcd(a,b,d,x,y); if(c%d !=0) { cout << "FOREVER\n"; } else { long long ans = x * c/d; //最小解 long long temp = b/d; ans = ans % temp +temp; cout << ans % temp << endl; } } return 0; }
Q3:阶乘的欧拉函数值(uva 11440)。
给出整数n , m,n∈[2,10^7],n≥m≥1,n-m≤10^5.那么请问[2,N!]有多少个x满足下列的性质,x的所有素因子都大于M.
分析:


参考代码如下:
#include<cstdio> #include<cstring> #include<cmath> using namespace std; const int maxn = 10000000 + 5; const int MOD = 100000007; int vis[maxn] , phifac[maxn]; void gen_primes(int n) { int m = (int)sqrt(n+0.5); int c = 0; memset(vis, 0, sizeof(vis)); for(int i = 2; i <= m; i++) if(!vis[i]){ for(int j = i*i; j <= n; j+=i) vis[j] = 1; } } int main() { int n , m; gen_primes(maxn); phifac[1] = phifac[2] = 1; for(int i = 3;i < maxn;i++) phifac[i] = ((long long)phifac[i-1] *(vis[i] ? i : i - 1)) %MOD;//题设给出取余运算MOD,中间过程一定要小心不要溢出。 while(scanf("%d%d",&n , &m) && n) { int ans = phifac[m]; for(int i = m + 1;i <= n;i++) ans = (long long)ans*i%MOD; printf("%d\n",(ans - 1 + MOD)%MOD); } return 0; }
Q4(uva 1363):
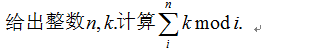
分析:这道问题表面上看起来很直观,似乎线性的枚举一遍然后加和即可,但是这个问题n的最大值是1000000000,所以即便是O(n)时间复杂度,也是要超时的。
所以我们需要利用数学技巧继续降低时间复杂度。


Q5(uva 10214):
在笛卡尔系下给出参数a,b,在[-a,a],[-b,b]的矩形区域内,除了原点,其余的整数对都种植树木,那么现在站在原点,问能够看到多少棵树?
分析:


参考代码如下:
#include<cstdio> #include<cmath> using namespace std; int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } int phi(int n) { int rea = n; for(int i = 2;i*i <=n;i++) if(n%i == 0) { rea = rea - rea/i; do n /= i; while(n%i == 0); } if(n > 1) rea = rea - rea/n; return rea; } long long fun(int a ,int b) { long long ans = 0; for(int i = 1;i <= a;i++) { int k = b/i; ans += k * phi(i); for(int j = k*i + 1;j <= b;j++) if(gcd(i , j) == 1) ans++; } return (ans * 4 + 4); } int main() { int a , b; while(scanf("%d%d",&a , &b) == 2 && a) { long long K = fun(a , b); long long N = (long long)(2*a + 1) * (2*b + 1) - 1; //运算细节,a b为int在运算过程中可能造成溢出,强制转换成longlong printf("%.7lf\n", (double)K / N); } }
Q6(uva 10820):
在某个具体问题中,两个参数组成的有序对(x,y)的值和(k*x,k*y)是一样的,那么现在给出另一个参数n,满足x≤n,y≤n的情况下,我们应该求多少组有序对的解?
分析:这个题目和上面在坐标系下种树的问题非常相似,我们需要求的解的数目,就是满足x≤n,y≤n,且gcd(x,y)=1的有序对(x,y).
既然有互素的关系,我们自然而然想到欧拉函数。
首先我们不考虑(1,1)(因为它是所有解中唯一一个横纵坐标相同的.),由于这里整数对(x,y)的顺序,即(x,y)和(y,x)是两种情况,但是考虑对称性,我们令x<y,求得结果然后乘2,再加上(1,1)这种情况即可.

Q7(uva 12169):
已知一个长度为2T的序列x[]的奇数项x[1],x[3],…,x[2T-1],还知道这个序列满足模运算递推公式:x[i] = (ax[i-1] + b) mod 10001,那么输出这个序列的x[2],x[4],…,x[2T].
分析:由于参数a、b是未知的,这里也没有太好的数学方法进行转化,考察a、b的范围是0到10000,因此我们只需枚举所有可能情况(a,b),然后反过来判断是否能够得到符号要求的x[1],x[3],…,x[2T-1]的数值即可。
参考代码如下:
#include<cstdio> #include<cstring> #include<iostream> using namespace std; const int maxn = 10000 + 5; const int maxt = 205; const int MOD = 10001; int x[maxt]; int T; void solve() { bool ok; int a , b; for(a = 0;a < maxn ;a++) for(b = 0;b < maxn;b++) { ok = true; for(int i = 2;i <= 2*T;i = i + 2) { x[i] = (a*x[i-1] + b)%MOD; if(i + 1 <= 2*T && x[i+1] != (a*x[i] + b)%MOD) {ok = false;break;} } if(ok) return; } } int main() { while(scanf("%d",&T)!=EOF) { int i = 1; for(int i = 1;i <= 2*T-1;i = i+2) //while(T--)的写法非常危险 cin>>x[i]; solve(); for(int i = 2;i <= 2*T;i = i + 2) cout<<x[i]<<endl; } }
Q8(uva 12716):
给出整数n(范围在[1,30000000]),询问有多少个整数对(a,b),满足gcd(a,b) = a XOR b.该问题认为(a,b)和(b,a)是一种情况。
分析:


#include<cstdio> using namespace std; const int maxn = 30000000 + 1; int cnt[maxn]; int sum[maxn]; void init() { for(int c = 1;c <= maxn;c++) for(int a = 2*c;a <= maxn;a += c) { int b = a - c; if(c == (a ^ b)) cnt[a]++; } sum[1] = 0; for(int i = 2;i <= maxn;i++) sum[i] = sum[i-1] + cnt[i]; } int main() { init(); int T; scanf("%d",&T); int tt = 1; while(T--) { int n; scanf("%d",&n); printf("Case %d: %d\n",tt++,sum[n]); } }
Q9(uva 11582):
给出a、b、n,(a,b∈[1,2^64],n<1000)求解斐波那契数列第a^b项对n取余的结果.
分析:直观来看这道问题并不抽象,但是有a、b太大使得我们不能够线性的求斐波那契数列在n剩余系下的结果.
结合斐波那契数列的递推关系,和容斥原理,我们容易看到,在n剩余系下的斐波那契数列、长度为n^2的斐波那契数列,必然存在不等于0的i,满足F[i] = 0 , F[i+1] = 1.这表明在n剩余系下的斐波那契数列必然存在周期性,我们只需要求得这个周期t。然后用快速幂得到a^b%t就可以解决这个问题了。剩下的就是编程技巧的问题了。
#include<cstdio> #include<iostream> using namespace std; typedef unsigned long long ULL; const int maxn = 1000 + 5; int F[maxn][6*maxn]; int period[maxn]; int pow_mod(ULL a, ULL b, int n) {//常规的参数为longlong的快速幂在这里会出错. if(!b) return 1; int k = pow_mod(a, b/2, n); k = k * k % n; if(b % 2) k = k * a % n; return k; } int solve(ULL a , ULL b , int t , int n) { if(a == 0 || n == 1) return 0; int p = pow_mod(a % t , b , t); return F[n][p]; } int main() { for(int n = 2;n < maxn;n++) { F[n][0] = 0;F[n][1] = 1; for(int j = 2;;j++) { F[n][j] = (F[n][j-1] + F[n][j-2])%n; if(F[n][j] == 1 && F[n][j-1] == 0) { period[n] = j - 1;break; } } } ULL a , b; int n; int t; scanf("%d",&t); while(t--) { cin>>a>>b>>n; cout<<solve(a , b , period[n] , n)<<endl; } }
Q10(uva 10375):
给出整数p,q,r,s(最大值为10000),让你计算下面的式子:
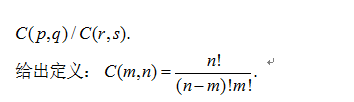
注意在原题描述中,dividing A by B的意思就是A/B,对于英语不好的读者这里可能产生歧义,输出结果不会超过10^8.
分析:考察p,q,r,s的最大值,不论是用阶乘定义还是帕斯卡公式得到的组合数都会无比巨大,但是结果在没有取模的情况下却是int类型以内的,这就说明我们不能整体的看这个式子,我们要在计算过程中就完成约减。
这里就用到了素数分解定理。
首先我们容易找到1~10000的素数表:
Prime[i]:
2 3 5 7 11…
然后有
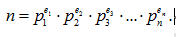
我们就得到了n经过素数分解后的指数表:
Prime_ex_list[]:
e1 , e2 , …...
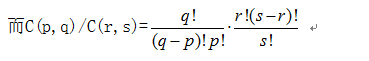
我们也是容易对n!进行素数的分析,进行六次,均在指数表的基础上进行,然后最终我们线性的扫一遍指数表,进行累乘即可。
参考代码如下:
#include<cstdio> #include<cstring> #include<cmath> using namespace std; const int maxn = 10000 + 5; bool isprime[maxn]; int prime[maxn],nprime; void doprime() // prime[1]~prime[nprime]记录[1,N]区间的所有素数 { long long i , j; nprime = 0; memset(isprime,true,sizeof(isprime)); isprime[1] = 0; for(i = 2;i < maxn;i++) { if(isprime[i]) { prime[++nprime] = i; for(j = i+i;j < maxn ;j += i) { isprime[j] = false; } } } } int prime_ex_list[1500];//函数功能:质因分解,得到整数n=p1^e1 * p2^e^2...的指数表{e1,e2,e3...} void prime_resolve(long long n , int d) { for(int i = 1;i <= nprime; i++) { while(n%prime[i] == 0) { prime_ex_list[i] += d; n /= prime[i]; } if(n == 1) break; } } void prime_resolve_fac(long long n , int d)//函数功能,对n!进行质因数分解,得到指数表{e1,e2,...} { for(int i = 2;i <= n;i++) prime _resolve(i , d); } int main() { doprime(); //printf("%d" , nprime); int p , q , r , s; while(~scanf("%d%d%d%d" , &p , &q , &r , &s)) { memset(prime_ex_list , 0 , sizeof(prime_ex_list)); prime_resolve_fac(p , 1); prime_resolve_fac(s , 1); prime_resolve_fac(r-s , 1); prime_resolve_fac(q , -1); prime_resolve_fac(r , -1); prime_resolve_fac(p-q , -1); double ans = 1; for(int i = 1;i <= 1300;i++) ans *= pow(prime[i] , prime_ex_list[i]); //attention ! prime_ex_list[] means n = Π(pi ^ ei) printf("%.5lf\n" , ans); } return 0; }
Q11(hdu 5916):

分析:首先我们解释什么是严格第k小,就是说k=1,可能有多组全排列都满足m的值最小,k=2时,我们利用去哪排列求得的m必须严格的比k=1的所有情况都大.
基于对题目的理解,我们可以进行巧妙的构造。
当k=1时,我们容易看到1,2,…,n必然是满足k=1的结果,而k=2的时候,我们只需要在全排列前面防止两个最大公约数是2的整数,紧接着我们排成一个n-2的全序列放在这两个整数的后面,使其满足整个序列除了a1和a2的最大公约数是2,剩下的部分,均满足相邻的两个整数是互素的。这样我们求m值,则必然比k=1时的m值大1,因此我们得到的排列必然是m值第2小的全排列。
而对于构造的细节,对k进行奇偶性的分析:
k是偶数的时候,2k,k,1,2,…,k-1,k+1,…n就是满足情况的序列。
k是奇数的时候,2k,k,1,2,…k-1,2k-1,2k-2,…,k+1,2k+1,…,n就是满足情况的序列。
参考代码如下:
#include<cstdio> using namespace std; int main() { int n , k; int t; scanf("%d",&t); int tt = 1; while(t--) { int n , k; scanf("%d %d" , &n , &k); printf("Case #%d: %d %d" ,tt++ , 2*k, k); if(!k%2) { for(int i = 1;i <= n;i++) { if(i == k || i == 2*k) continue; printf(" %d" , i); } } else { for(int i = 1;i <= k - 1;i++) printf(" %d" , i); for(int i = 2*k - 1;i >= k + 1;i--) printf(" %d" , i); for(int i = 2*k + 1;i <= n;i++) printf(" %d" , i); } printf("\n"); } }
Q12(hdu 5979):
给出a,b,其中a、b满足下面的式子:
X+Y=a , LCM(X,Y)=b,现在让你求X、Y.
分析:拿到这种题目,第一意识不应该是暴力穷举,这种结合数论概念的题目往往可能存在非常

#include<cstdio> #include<cmath> using namespace std; typedef long long LL; LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a%b); } int main() { LL a ,b; while(~scanf("%lld%lld" , &a , &b)) { int flag = 1; LL G = gcd(a , b); LL temp = a*a - 4*G*b; if(temp < 0) {flag = 0;} else if((LL)sqrt(temp) * (LL)sqrt(temp) != temp) {flag = 0;} else if(((LL)sqrt(temp) + a)%2) {flag = 0;} if(!flag) printf("No Solution\n"); else { LL x = ((LL)sqrt(temp) + a)/2; LL y = a - x; printf("%lld %lld\n" , y , x); } } }
Q13(uva 11388):
给出G=gcd(a,b),L=lcm(a,b),计算整数对(a,b),其中a小于b,有多解时取a最小的那组解.
分析:用到gcd和lcm的基本概念这道问题进行简单枚举即可。
L=Ga’b’,gcd(a’,b’)=1.
当L/G是整数,从小到大枚举a’,然后得到b’.
当L/G不是整数,无解。
参考代码如下:
#include<cstdio> #include<iostream> using namespace std; int main() { int G , L; int t; cin>>t; while(t--) { cin>>G>>L; if(L%G) cout<<-1<<endl; else { int temp = L/G; int i; for(i = 1;;i++) if(!(temp%i)) break; cout<<i*G<<' '<<G*(temp/i)<<endl; } } }
Q14(uva11426):

参考代码如下:
#include <cstdio> //O(nloglogn) #include <cstdlib> #include <cstring> #include <cmath> using namespace std; const int SIZE = 4000000 + 5; int phi[SIZE]; long long f[SIZE]; long long S[SIZE]; void phi_table() { int i, j; memset(phi, 0, sizeof(phi)); phi[1] = 1; for(int i = 2; i < SIZE; i++) if(!phi[i]) { for(j = i; j < SIZE; j+=i) { if(!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i-1); } } } int main() { phi_table (); for(int i = 1;i < SIZE;i++) for(int n = i + i;n < SIZE;n += i) f[n] += i*phi[n/i]; //printf("%d\n" , f[2]); S[2] = 1; for(int i = 3;i < SIZE;i++) S[i] = S[i - 1] + f[i]; int n; while(~scanf("%d" , &n) && n) printf("%lld\n" , S[n]); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号