《训练指南》——7.27
最优排序二叉树问题:
给n个符号建立一个排序二叉树。给出n个字符的频率f1,f2,…fn,求解二叉树总检索次数最小为多少?
注:1.总检索次数是每个字母出现的频率乘以它所在树结构中的深度的和。
2.建树过程中需要注意的是,n个符号的序列的顺序是隐藏了信息的,举个例子来说,我们选取第k个字母作为根,那么序列中该字母左边的字母均为它的左子树,该字母右边的字母均为它的右子树,知道了隐藏的这点信息将会简化问题难度。
分析:
子问题化:很典型的基于区间上的dp问题,我们常用的子问题方法就是选取一段区间,即设置dp[i][j]表示用字母序列第i~第j(包括第i、j个)之间的字母建立的最优二叉树。
那么基于注2.的理解,我们可以遍历[i,j]中的任何字母作为根节点,这样我们便能够找到当前问题的所有子问题,并且保证了子问题与当前问题的相似性。
状态的转移:假设当前我们选出了某个下标为k的字母作为根,能够看到,基于两个子问题(也就是左右子树)dp[i][k-1],dp[k+1][j],我们以第k个字母为根,导致左右子树上的所有元素在树中的结构都加深了一层,也就是如下状态转移方程所描述的:
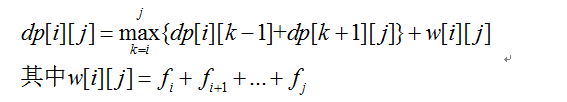


 浙公网安备 33010602011771号
浙公网安备 33010602011771号