《训练指南》——7.26

  点集配对问题：

  空间中有n个点P[0]、P[1]、P[2]、P[3]、P[4]……P[n-1]，把它们配成n/2对(n是偶数)，使得每个点恰好在一个点对中。要求所有点对中，两点的距离之和应尽量小。

  分析：举一个具体的例子，然后推广到一般形式。

  对于序号是1、2、3、4、5、6这六个点，我们如何对其进行子问题化然后形成状态转移方程呢？很简单，这个问题可以分解成如下的情况：

  (1)1、2点配对，然后考察3、4、5、6四个点之间形成点对距离之和的最小

  ……

  然后其实就是C(6,2)的组合问题了。

  这里我们用S集合用来表示点集，用dp[S]来记录完成S集合中配对的最优解，那么我们很容易得到如下的状态转移方程。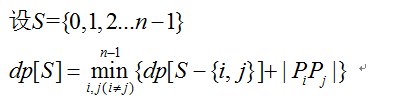         

  可以看到，这里既然用到了集合，那么在实际编程中就需要用到状态压缩的技巧，即用一个而二进制数来表示集合进而简便的来表征一个参数。