《数学竞赛辅导》-一元函数微分学-7.23
这个专栏用于博主备战16年9月的全国大学生数学竞赛(非数学)的习题集,因此在记录过程中以题目为主,几乎不会呈现理论定理的推导过程。
这篇文章用于记录一元微分学相关的题目。所谓一元微分学就是一个变量的函数,进行多次求导,相应的一元积分学就是一元函数多次积分,改变变量的个数就是多元函数微分学、多元函数积分学,这个在陈启浩的《大学生数学竞赛指导(非数学)》中的目录中给出,对于梳理知识体系会有一定的帮助。
微分,也就是我们常说的求导,就是一种极限条件下的无线分隔,因此这里题目中我们必不可少的将会与极限联系起来。
Ex2.1:
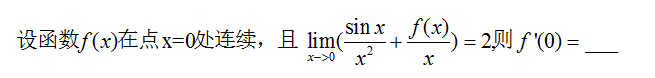
分析:显然我们要极限式中挖掘更多的信息,观察到它的分母是趋于零的,那么根据极限法则,我们将会得到分子也将趋于0,随后再结合导数的定义,进行计算。
解:
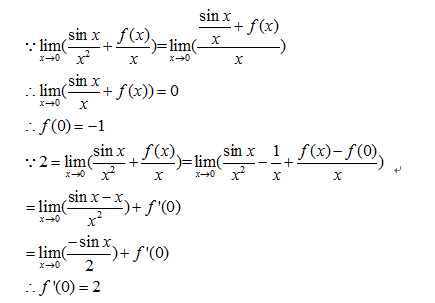
可以看到,这个过程用到极限法则、导数在x0处的定义以及洛必达法则。
Ex2.2:
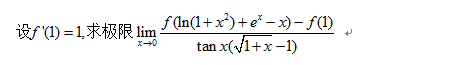
分析:这里仅仅给出了f(x)在一点的导数值,其余点的导数值我们不得而知,因此这里不能贸然的用洛必达法则,还是考虑通过巧妙的等价转化将其往导数定义上靠拢。
解:
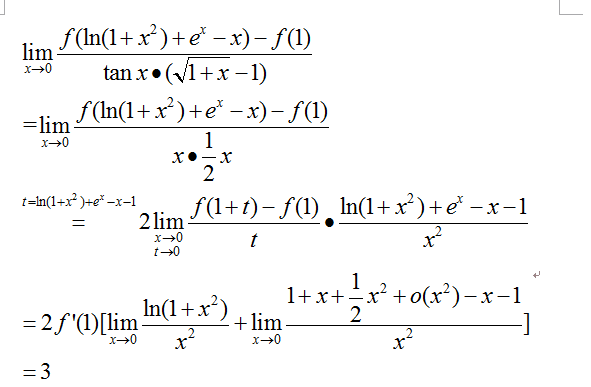
可以看到这个过程涉及的技巧有适当的代换(凭此构造出导数的定义式),利用等价无穷小简化极限式子(这个几乎贯穿了竞赛中有关极限计算的题目中),然后最后还利用了泰勒展开的公式。
这里开始有意识的积累一些等价无穷小的公式:
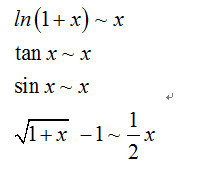


 浙公网安备 33010602011771号
浙公网安备 33010602011771号