《算法问题实战策略》-chaper8-动态规划法
Q1:偶尔在电视上看到一些被称为“神童”的孩子们背诵小数点以后几万位的圆周率。背诵这么长的数字,可利用分割数字的方法。我们用这种方法将数字按照位数不等的大小分割后再背诵。
分割形式如下:
所有数字都相同——难度为1——示例:3333,555
数字逐个单调递增或递减——难度为2——示例:23456,3210
两个数字交替出现——难度为4——示例:323,54545
等差数列——难度为5——示例:147,8642
其他情况————难度为10——示例:17924、331
那么现在给出一定位数的圆周率,按3到5位数字分割,使南都之和变为最小。请编写程序计算最小难度。
分析:很典型的要用到动态规划的问题,给出一个整数串N,其长度是L。我们设置一维数组dp[i]记录整数串第i位到最后这段序列最优分割下的最小难度和,那么dp[1]便是问题的最终解。
子问题化建立递推方程:为了求解dp[L],结合“按3到5位数字分割”的限制条件,我们容易将其分割成如下的三个子问题。
(1) 取前三位计算难度,加上dp[4].
(2) 取前四位计算难度,加上dp[5].
(3) 取前五位计算难度,加上dp[6].
我们利用Fun(i,j)函数来计算N序列中N[i]~N[j]这一区段的难度,则通过归纳,我们能够得到如下的递推方程式:
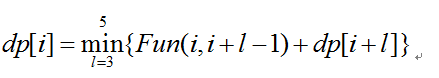
那么到了这个层面,剩下的就是模拟实现函数Fun(i,i+l-1)了。
概率与所有可能的个数有着密切关系,所以计算概率的问题中也能用得上动态规划。
Q2:爬出水井的蜗牛.
现在有一口n米的水晶,身处水井底部的蜗牛想要爬到井口。不过蜗牛的行进速度是受到天气影响的。天气好时,蜗牛一天前进2米,天气不好的时候,蜗牛一天行进1米,那么请问,在m天后,蜗牛能够爬到井口的概率是多少?(对于某一天,天气是好是坏的概率各占1/2)
分析:既然是求概率,我们需要知道基本事件空间,显然对于蜗牛,m天的行程共有2^m种走法,那么现在我们关注的就是,有m天中有多少种方案,蜗牛的行程行程综合是大于n的?
子问题化:容易看到上述问题中给出了两个参量,因此我们就利用二维数组dp[i][j]来表征整个过程的分状态,设dp[i][j]表示蜗牛前i天走了j米的不同路径数,则我们容易得到如下的状态转移方程:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j-2].
那么题目的最终答案即:
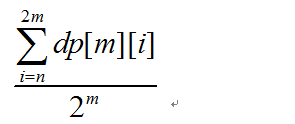
可能有人注意到了,这道问题对于天气概率的平均分配,为我们解题提供了遍历,但是如果说某一天天气分布的概率不是均等的,那么这个问题应该如何处理呢?
雨季来临:
如果说每一天的天气情况分布不再是均等的,下雨的概率变成0.75,那么这个问题该如何求解呢?
有过概率论基础的同学会发现,如果还按照上面的计算过程,我们得到的是期望值,然而期望值对于这里题目的求解并没有太大的帮助,因此我们应该考虑转换一下每个状态中存的数值含义,如果定义dp[i][j]表示前i天爬了j米的概率,结合基本的分步乘法原理那么我们可以得到如下的状态转移方程:
dp[i][j] = 0.75dp[i-1][j-1] + 0.25dp[i-1][j-2].
那么很显然,问题的最终答案是如下的式子:
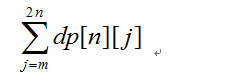
Q3:
多米诺铺设方案数问题:
现在有1x2的多米诺方块n个,那么将这些方块填充在宽度为2的槽中,有多少种不同的方案?这些方案中非对称的有多少种?
分析:第一小问很好回答,这里我们设dp[n]是这道问题的答案,那么有递归方程如下:
dp[n] = 2dp[n-2] + dp[n-1]
对于第二小问,我们面临的问题是如何求出n个1x2多米诺拼出对称型的方案即可,对于n个1x2多米诺牌,n奇偶性决定了对称方案数的计算方法。设置dp1[n]表示n对称的填充方案数。
(1) 如果n是奇数,它的对称轴必然是一个竖置的多米诺,那么dp1[n] = dp[(n-1]/2]
(2) 如果n是偶数,它的最中央是两块横置的多米诺或者两块竖置的多米诺,那么dp1[n] = 2dp[(n-2)/2]
Q4:
其实基于最基本的dp模型,有一类变式我们可称其为“双重dp”,举个例子,像LIS、数字三角形这种原始的dp模型,往往再加一重问题,LIS问题中最长上升子序列的长度是m,那么所有长度为m的最长上升子序列有多少?数字三角形权值最大是m,那么权值为m的不同路径有多少?
分析:关于LIS的这个变式我们在相应的专题中曾经涉及过,这里便不再赘述。这里主要分析一下数字三角形中的最优路径数的问题。
我们先从直观的递归公式开始,尽管它在实际编程中会相对递推耗费双倍的时间,但是它呈现的状态转移关系是相对清晰直观的。在具体的实践中,先写出递归关系式然后改写成递推公式不失为一种好的方法。
设置dp[i][j]是数字三角形中位置坐标为(i,j)的点,到达数字三角形最底层的最优路径的个数,dp0[i][j]记录从(i,j)开始到达最底层的最优路径的权值和。那么我们从dp[0][0]往下一层找,很容易得到如下的状态转移方程:
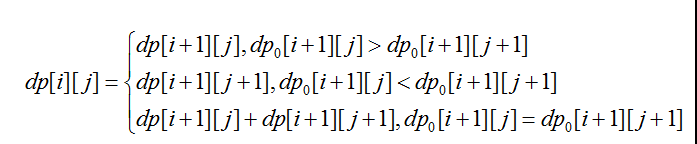
很容易看到这个过程其实是依附于dp0[i][j]的求解过程的,因此也不难将其改成递推形式。
Q5:
多联骨牌:
把正方形的边互相连接而形成的图形称为多联骨牌。用n个一样的正方形组成多联骨牌,其中纵向单调的多联骨牌会有多少个?纵向单调是指任何横线都不会与多联骨牌发成两次以上的交叉,再通俗一点的说,每一行中间的小正方形都是紧密的排成一排,两个小正方形中间是不会有空隙的。
分析:这道问题的关键是子问题化,对于规模是n的多联骨牌,我们如何将其规模缩小呢?很容易想到,我们枚举多联骨牌第一行小正方形的数量,这里用一个参量first记录,但是这里问题在于,仅限于此好像无法实现状态的转移,因为first个小正方形还会与第二行形成已知数目的组合情况,因此很自然的,我们还要枚举第二行的小正方形数目,这里我们用变量second记录。那么在这种情况下,第一行和第二行有first + second – 1种拼接方法(因为其必须满足纵向单调的限制)。
设置dp[n][first]来表示n个小正方形,并且第一行是first个小正方形,对于dp[n][first],我们很容易看到有如下的递归方程式:

而该问题的最终答案即:
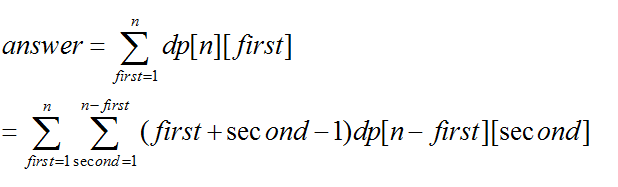
Q6:
合并LIS:两个整数序列A和B,我们分别取出这两个序列中的上升子序列,合成一个严格上升的序列,我们将其视为合并上升子序列,那么所有的合并上升子序列中,最大的长度是多少呢?
分析:
不能用贪心算法。拿到这个题很多人容易想求解两次LIS然后相加,但是结合题目要求的“最长合并严格上升子序列”,我们发现这种贪心做法并不合适,因此我们需要用做一维整数数组的LIS问题来做这个二维整数数组的LIS问题。
子问题化:对于区间上的问题,我们进行子问题化的方法往往是以下标作为基础,这里也是一样,我们设置dp[i][j]表示以A数组第i个元素、B数组第j个元素结尾的最长合并严格上升子序列的长度。
递归公式:这里和一维LIS最主要的区别就是对于两个序列的上升子序列中重复元素的处理,能够看到,对于dp[i][j],如果我们想要缩减其规模,必须有所保证,例如对于k<i,有A[i] > A[k],只有当A[i]>B[j]的时候,我们方能放心大胆的将dp[k][j] + 1视为dp[i][j]的一个子状态(但不一定是最优子状态),那么如果A[i]=B[j]或者A[i]<B[j]呢?我们显然不能够还想上面那样表示子状态,因此我们在写状态转移方程的时候应该有上面这样一个分情况讨论然后确定子状态的问题。
对于A[i]=B[j]这种出现重复元素的情况,那么很显然我们就不能去+1了。
对于A[i]<B[j]这种情况,我们进行对称性思考我们想要那么我们很容易得到如下的状态转移方程:
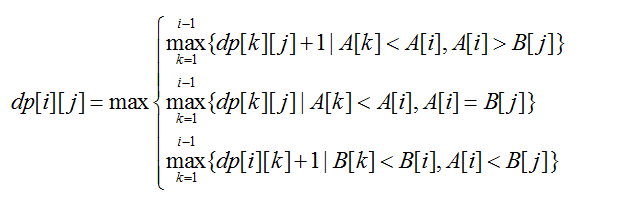


 浙公网安备 33010602011771号
浙公网安备 33010602011771号