《University Calculus》-chaper12-多元函数-拉格朗日乘数法

  求解条件极值的方法：拉格朗日乘数法

  基于对多元函数极值方法的了解，再具体的问题中我们发现这样一个问题，在求解f(x,y,z)的极值的时候，我们需要极值点落在g(x,y,z)上这种对极值点有约束条件，通过直接代换消元的方法似乎会出现一些问题。

  比如这个例题。

 

  它面临的问题是，代换消元然后通过求偏导得来的驻点，我们无法控制其满足约束条件g(x,y,z)，因此我们需要寻找新的方法来解决这种条件极值问题。

  首先这里给出方向导数和梯度中给出的等式关系，这个具体的由来我们会在该小结中详细介绍。

  对于可微函数f(x,y,z)，有如下关系成立：

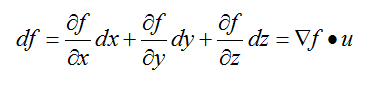                                   (1)

  那么现在假设有一条曲线C的参数形式为r(t) = g(t)i + h(t)j + k(t)k(这里相当于是限制函数)，则我们很自然的能够得到如下关系式：

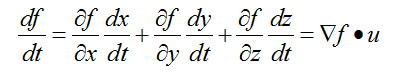                               (2)

  此时我们已经把待求极值函数和约束条件联系了起来，下面我们则要利用极值点这个条件了。某点P落在限制函数曲线g(x,y,z)上，从结果出发，假设P是极值点，利用其必要条件，有(2)为0.即梯度f和任意方向向量正交。

  上面这个过程其实是一个定理，叫做正交梯度定理。

  随后再基于方向梯度一节当中的一个原理：梯度g和同层曲面g=0是正交的(详细的解释我们在这一小节的文章中会给出)，因此我们能够看到，梯度f和梯度g能够同时正交于一个方向向量，结合P点落在限制函数曲线g(x,y,z)上的条件，我们得到如下两个等式：

   

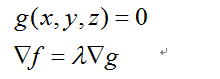
  即我们求解满足上述方程组的参数x0、y0、z0、λ，（x0,y0,z0）即为驻点。这就完美的解决了代换所引起的对约束函数的利用不足了。

  这就是拉格朗日乘数法的原理。