《程序设计中的组合数学》——容斥定理
在中学阶段的数学中,有诸如“一个班有7个语文满分,6个数学满分,5个英语满分……求满分的同学有多少个”的“多面手”问题,当时老师介绍的思路是画个图自己分配一下,上了大学才知道有个容斥原理能够秒杀这类的所有问题,瞬间感觉高中学的东西好low……
容斥原理在理论上很好理解,就给一个最简单的模型——一个班5人数学满分、7人英语满分、3人数学、英语满分,那么这个班满分的人数是多少?答案是显而易见的——5 + 7 - 3= 9。 明白了这个简单模型,便可以给出容斥原理最简单的形式。
而问题来了,这里我们讨论了具有P1、P2两种性质的∪,那么3种、4种乃至更多呢? 这种简单的容斥原理的推广形式是怎样的呢? 在这里不需要引入代数计算,稍微用脑子想一想就可以进行推广。在容斥原理简单形式中,我们从实际意义来分析这个式子,不过是把满足2个性质的集合加起来(这里这两个集合如果有交集,那么就加了两次),然后减去这两个集合的交集,就会得到我们想要的A∪B。而如果要给出满足P1、P2、P3性质的集合,依然重复上述过程,但是你会发现,你在减掉任意两个集合(假设这里取A,B、A,C)的交,如果A、B、C是有交集的,那么你在减去A、B,A、C的∩的时候,实际上你减掉A∩B∩C两遍,因此你还要加上一个A∩B∩C,这里分析了一种情况,在推广后的公式只需引入Σ符号进行遍历即可。 于是我们得到容斥定理如下的一般形式。 

可以看到,书中构造了一个函数来区别两种不同的相交情况。其实只需找到两个圆心距离小于1的情形就可以,在这道题上还是比较容易找到这两种情况,所以构建函数没有显现出太大的威力。
而对于三个圆的都相交情况,可以在上面两种情况下作图,找到满足三个圆都相交的情况,实际上,只有三个圆心在一个小正方形的三个顶点上在能满足这种情况。 
针对五个圆都相交的情况,继续在四个圆相交的情况下加圆心,发现无论如何都无法使得五个不重合的圆都相交,这显然是个重大的发现,因为这样在应用容斥原理公式的时候会得到大大的简化。
由上述过程不难得到容斥原理的计算表达式。 
有了数学层面的推导,在程序实现的时候应该就是一个遍历的模拟计算。由于笔者非常懒,而且杭电的oj居然没有这道原题,所以就不贴代码了。
来看一道关于容斥原理的简单应用。(Problem source : hdu 4135)
题目大意:给定一个区间[A,B],找出在这个区间内与给定的n互质的整数的个数。
数理分析:考虑到直接求互质的数是不太好实现的,我们不妨从它的反面思考,尝试算出这个区间与n非互质的整数的个数,那么再做一步减法运算即可得到最终的答案。而找到与n非互质的整数的个数,则可以通过先找到数字n的所有质因子,便可以得到区间上所有的非互质数,然后计算这些非互质数的时候可不是简单的加和,这里就用到了容斥原理。
概括起来,是一下几个步骤。
1.找到数字n的质因子,并可以因此求出那些与n非互质的数。(涉及初等的数论)
2.找到在指定区间上与n非互质的个数。(涉及容斥原理) 3.做一步减法运算,得到互质的个数。
举个栗子,如果你给定的区间是1到10,n = 2.
1. 2的质因子是2.在这个区间上非互质的数字即2 4 6 8 10
2. 区间上非质因数有5个
3. 质因数就有10 - 5 = 5.
这是一个初步的数理分析,在算法实现上还有一些需要注意的问题。比如说容斥原理的实现(这里给出队列数组实现,还有位运算和深搜可以实现);由于给出的是区间,而不是[1,y],所以在处理步骤三的时候并不是一个简单的相减。
代码如下:
#include<stdio.h> __int64 a[1000] , num; void find(__int64 n) //考虑数据都比较大,这里全程用__int64 { //函数功能:找到n的所有质因子 __int64 i; num = 0; for(i = 2;i*i <= n;i++) //这里for两个;中间的判断条件为什么有等号?而又为什么临界点是根号n? { if(n % i == 0) { a[num++] = i; while(n % i == 0) n /= i; } } if(n > 1) //如果没有除尽,说明n的质因子是它本身 a[num++] = n; } __int64 haha(__int64 m) { __int64 i , j , k ,que[1000] , sum ,t = 0; que[t++] = -1 , sum = 0; //依据容斥原理,que[0]的值是-1 for(i = 0;i < num;i++) { k = t; for(j = 0;j < k;j++) que[t++] = que[j]*a[i]*(-1);//这里是实现容斥原理的精髓,大脑模拟一下在结合容斥原理就会明白 } for(i = 1;i < t;i++) sum += m / que[i]; return sum; //返回值是[1,m]的非互质的个数 } int main() { __int64 i,T , x , y , n ,sum; while(scanf("%I64d",&T) != EOF) { for(i = 1;i <= T;i++) { scanf("%I64d%I64d%I64d",&x , &y , &n); find(n); sum = y - haha(y) - (x - 1 -haha(x - 1)); //由于区间是[x,y],求出[1,y]的互质个数,再减去[1,x-1]的互质个数 printf("Case #%I64d: ",i); printf("%I64d\n",sum); } } return 0; }
再来看一道与之很类似的一道题目。(Problem source : hdu 1796)
题目大意:这道题是说,给你一n,然后再给你一个有m个元素的序列,让你算算小于n并且能被这m个元素中整除的整数有多少个。
显然这里容斥原理体现得还是比较明显的,只不过穿插了一些数论的小知识。对应于容斥原理的第一个西格玛后面的西格玛,这里多个元素的∩其实表示的是多个元素的最小公倍数,而在计算多个元素的最小公倍数的时候,下面还会涉及一些技巧。 编程实现上,上题用到了队列数组,这道题我们尝试利用深搜(dfs)来构造一下。 而编程实现的重点,就是你如何设计算法遍历每一种组合情况(容斥原理给出的公式,需要减掉所有的Ai∩Aj,如何实现这一层遍历便是编程实现容斥原理的精髓所在。)
我们可以设第一层穷举,遍历的是组合情况含有的元素个数。假设我们当前在找的是i个元素组成的情况,下面要做的便是设计一个深搜算法来遍历出所有i个元素的组合情况。这里模拟的其实就有点类似小学我们常提到的n个点能组成多少条线段(找出两两组合的数量,而这里就要找出i个元素组合在一起的数量),用到了回溯的算法思想。通过dfs,我们可以构建出一个树,它将遍历到所有情况。 值得注意的是,这里在求得i个元素的最小公倍数是有点难度的,我们需要将问题进行分解,如果求两个数字的最小公倍数,我们常用的方法是先求出最大公约数(辗转相除),然后最大公约数、最小公倍数、还有这两个数字是有一定的联系的,利用等式便可导出最小公倍数,有了这层思路,我们在求解i个元素的最小公倍数的时候,可以先求两个,再和第三个求,再和第四个求,这样一直保持是两个数字在求最小公倍数,这样整个程序就显得十分的简洁,实际上,这与后面dfs一步一步构造出i个元素的组合情况也是自洽的,dfs一步一步构造出i个元素的过程中,实际也是在两个数字两个数字地求最小公倍数。
有了这层分析,再看代码就会更好地理解了。
#include<stdio.h> int a[15]; int num , ans; int n , m; int i ,temp; int gcd(int a,int b) //辗转相除求两个数的最大公约数 { if(!b) return a; else return gcd(b ,a%b); } void dfs(int number, int situation , int need_element ,int now_element)//number表示每次求得的最小公倍数 { int i; //situation表示当前遍历到的位置,在[1,n]上,它的存在是提到标记作用 if(now_element > need_element) return; if(now_element == need_element) //如果当前构造出的元素个数与需要的元素个数一样,那么开始计数 { if(now_element%2) //如果余2等于1,那么显然是奇数个元素,在容斥原理的公式中符号位是+ ans += n / number; else ans -= n / number; //元素个数是偶数个,符号位是- } for(i = situation + 1;i <= num;i++) //如果元素个数不够,那么继续遍历,从这次深搜定下的situation后一位开始继续,元素的个数也要加1 dfs(number / gcd(a[i],number)*a[i] , i , need_element , now_element + 1 ); } int main() { while(scanf("%d %d",&n,&m) != EOF) { num = 0 , ans = 0; n--; for(i = 1;i <= m;i++) { scanf("%d",&temp); if(temp != 0) a[++num] = temp;//之所以这样设置,是因为题目设那m个元素是非负的,因此需要考虑0的情况 } //题目认为0是不算的,个人认为这是原题存在的漏洞,并没提及0到底算不算进去 for(i = 1;i <= num;i++) //元素个数从1到num的遍历 dfs(1 , 0 , i , 0); printf("%d\n",ans); } }
再来看一道类似的题目,这次我们会用到位运算的方式来实现容斥原理。 (Problem source : hdu 4336)
As a smart boy, you notice that to win the award, you must buy much more snacks than it seems to be. To convince your friends not to waste money any more, you should find the expected number of snacks one should buy to collect a full suit of cards.
题目大意:这里牵涉到概率论上的一些基本概念——期望。根据我的理解,期望是通过概率进行相关的计算得出的具有实际物理意义的一个概念。就这题而言,我们给出每个元素出现的概率p,期望1/p则表示想要抽到这个元素需要的次数。(某个元素出现的概率是0.1,那么这里期望值便是10),而我们需要的是找到这n个元素在一起,求出期望。
数理分析:这里对于期望的理解是一个难点,它涉及一些概率论的理论性内容。上面解释了单个元素的期望值求法,那么两个元素呢?实际就是A1∩A2的期望值,而这里每个事件显然是互相独立的,那么A1∩A2显然等于A1 + A2,因此这两个元素的期望值应该是1/(A1 + A2),我们可以看到,A1的期望显然和A1∩A2的期望是有重叠部分,那么这里就解释了为什么会用到容斥原理了。
算法实现:有了以上的数理分析,我们面临的编程实现的困难就在于(dfs,队列数组的实现也是面临这个难题),如何遍历出容斥原理中给出的所有组合情况?也就是如何设计程序来跑完公式中的所有西格玛并且保证不重不漏。 我们知道,容斥原理的公式中给出是有一定的顺序的,奇加偶减,并且每个西格玛所含的元素是依次增加的,那么,最后会有多少种组合情况呢?假设有n个元素吧,它所有的组合情况便是2^n - 1(除掉0个元素的情况,这里涉及二项式定理的小知识),而c语言中刚好提供了位运算符“<<”帮我们方便的得到这个数字,同时,我们可以换一个视角看这个数字,如果我们遍历这2^n - 1 个数字,我们用01的思维去看待这些数字,也就是把数字转化成二进制,会发现每一位的数字可以表达丰富的物理含义(第i位是0,说明这种组合情况不包含第i个元素,反之则包含),这样我们便遍历出了所有的组合情况,随后我们只需在遍历一次这n个元素,并与当前情况进行匹配,我们就可以进行计算了。
代码如下。
#include<stdio.h> int main() { double element[25] , ans , sum; int i ,j; int n ,all; int odd; while(scanf("%d",&n) != EOF) { ans = 0; for(i = 0; i < n;i++) scanf("%lf",&element[i]); all = 1 << n; //2^n - 1,包含了所有的组合情况 for(i = 1;i < all;i++) { sum = 0 , odd = 0; //sum用于计算结果,odd用于记录当前有几个元素组合,以便实现计算的奇加偶减 for(j = 0;j < n;j++) { if((1 << j) & i) //遍历n个元素与当前的组合情况进行匹配 { odd++; sum += element[j]; } } if(odd & 1) ans += 1.0/sum; else ans -= 1.0/sum; } printf("%.6lf\n",ans); } }
让我们再看一道有关容斥原理的题目。(Problem source : hdu 2841)
If two trees and Sherlock are in one line, Farmer Sherlock can only see the tree nearest to him.
上面是一个简单的例子作为更好地理解这题的数理模型。下面便是编程实现。
值得一提的是,观察到这题的最大数据是100000,我们在找i的所有素因子的时候,需要考虑开多少列。这里提供前九个素数的乘积的结果:
代码如下。这题是利用dfs遍历出所有情况实现容斥原理的。
#include<stdio.h> int prime_factor[100005][10]; //记录所有数的素数因子 int number_of_prime_factor[100005] = {0};//记录所有数含有素数因子的个数 void Init() //埃及筛法完成上述过程 { int i ,j; for(i = 2;i <= 100000 ;i++) { if(number_of_prime_factor[i]) continue; prime_factor[i][0] = i; number_of_prime_factor[i] = 1; for( j = 2;i * j <= 100000;j++) prime_factor[i * j][number_of_prime_factor[i * j]++] = i; } } long long dfs(int m , int number, int now_element)//函数功能,找到[1,n]中与m非互质的整数的个数,now_element表示当前组合含有的元素个数。 { int i; long long number_of_no_coprime = 0; for(i = now_element;i < number_of_prime_factor[m];i++) number_of_no_coprime += number / prime_factor[m][i] - dfs(m , number/prime_factor[m][i] , i + 1); return number_of_no_coprime; } int main() { int t , i; int m ,n; Init(); scanf("%d",&t); while(t--) { scanf("%d %d",&n,&m); long long ans = n; for(i = 2;i <= m;i++) ans += n - dfs(i , n , 0); printf("%I64d\n",ans); } }
来看一道数论和容斥原理紧密结合的题目。 (Problem source : hdu 2204)
#include<stdio.h> #include<math.h> int prime[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59}; long long n; int i; long long ans; long long dfs(int now_element , int number , int need_element) //now_element表示素数表的下标来调用素数,构造指数 { //number表示当前构造出来的指数 if(need_element == 0) //need_element表示当前情况还需要几个元素构造才能进行容斥定理的计算,等于0标志开始进行容斥定理的计算 { long long temp = pow(n , 1.0/number); if(pow(temp , 0.0 + number) > n) temp--; //这是上文所说的加减运算,这里A^k大于n,那么A这个数就不要了 temp--; //都减掉1那种情况,因为它与所有情况都重合,最后输出结果会+1,与下面ans+1相呼应 if(temp > 0) ans += temp*(i & 1 ? 1 : -1); //容斥原理 return ans; } if(now_element == 17) //dfs一个剪枝过程 return; if(number * prime[now_element] < 60) dfs(now_element + 1 , number*prime[now_element] ,need_element - 1); dfs(now_element + 1, number ,need_element); //深搜遍历出所有组合情况 } int main() { while(scanf("%I64d",&n) != EOF) { ans = 0; for(i = 1;i <= 3;i++) //遍历到含有三个元素的情况 dfs(0 , 1 , i); printf("%I64d\n",ans + 1); } }
#include <string.h> #include <algorithm> #include <stdio.h> #include <iostream> using namespace std; typedef long long LL; const int N=1000005; const LL MAX=(LL)1<<62; bool prime[N]; LL p[N]; LL f[N]; LL k,cnt,num,ans,n,m; void isprime() { cnt = 0; int i,j; memset(prime,true,sizeof(prime)); for(i=2; i<N; i++) { if(prime[i]) { p[cnt++]=i; for(j=i+i; j<N; j+=i) { prime[j]=false; } } } } void Solve(LL m,LL n) { cnt=0; LL i; for(i=0; p[i]*p[i] <= n; i++) { if(n%p[i]==0) { f[cnt++]=p[i]; while(n%p[i]==0) n /= p[i]; } } if(n>1) f[cnt++]=n; for(i=0; p[i]*p[i] <= m; i++) { if(m%p[i]==0) { f[cnt++]=p[i]; while(m%p[i]==0) m /= p[i]; } } if(m>1) f[cnt++]=m; } void dfs(LL now_element , LL true_element , LL make , LL x) { if(now_element == num) { if(true_element & 1) ans -= x/make; else ans += x/make; return; } dfs(now_element+1 , true_element , make , x); dfs(now_element+1 , true_element+1,make*f[now_element],x); } LL Binary() { LL l = 1,r = MAX,mid,ret; while(l <= r) { mid=(l+r)/2; ans=0; dfs(0,0,1,mid); if(ans >= k) { ret = mid; r = mid-1; } else l = mid+1; } return ret; } int main() { isprime(); LL t,tt=1; scanf("%I64d",&t); while(t--) { scanf("%I64d%I64d%I64d",&m,&n,&k); printf("Case %d: ",tt++); Solve(m,n); sort(f , f + cnt); num=1; for(LL i=1; i<cnt; i++) { if(f[i]!=f[i-1]) { f[num++]=f[i]; } } printf("%I64d\n",Binary()); } return 0; }

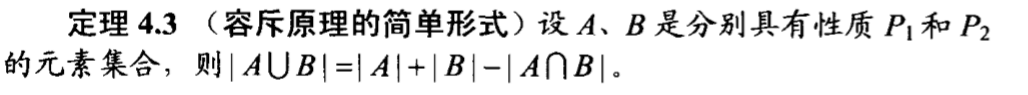



 浙公网安备 33010602011771号
浙公网安备 33010602011771号