数论及其应用——素数问题
数学是科学的女王,数论是数学的女王——高斯。
然后我再狗尾续个貂——素数是数论的女王。
谈及素数,可以牵扯出很多数学史上的美谈,例如前几天在知乎上看到关于“除去酒色,人类还怎么享受生活”的问题,在一个回答中就举个几个大科学家的例子,其中提到某个钟爱素数的数学家,选择再每月的素数天和妻子同居,一个月刚开始还好,但越到月末素数间隔变大,同居的日子也就变少。
在素数这块小地方,有很多著名的猜想,能证出来一些真的是非常非常的厉害,因为当今世界流传着这样一个传说,集齐七大世界数学难题,便可以召唤神龙,帮助你实现一个愿望。
扯远了,这里先介绍几个关于素数的猜想。
孪生素数猜想:存在无穷多的形如p,p+2的素数对。
1966年陈景润用复杂的筛法证明了存在无穷多对孪生素数,现在寻找孪生素数成为了一种趣味竞赛,目前最大的孪生素数对是33218925.2^169690 +1 , 33218925.2^169690 -1 。华人数学家张益唐在这方面有很杰出的成就。
哥德巴赫猜想:每个大于2的正偶数可以写成两个素数的和。
这个猜想是1742年哥德巴赫写给欧拉的信中给出,目前已经验证了所有小于4 * 10^14的偶数满足这一猜想。
n^2 + 1猜想:存在无穷多个形如n^2 + 1的素数,其中n是正整数。
人们不仅对素数的形式着迷,也热衷于探索素数的分布规律。这里我们引出素数定理——设π(x)为小于整数x的素数个数,那么随着x的增大,有π(x) = x/lnx。由于时间原因,这里暂且不探讨证明过程。
那么基于这个定理,我们来解决一个实际的问题。(Problem source : nufu 117)

针对这个问题如此大的数据量,我们显然无法直接运算,那么就要用到我们的素数定理里。但是这里需要注意的是,这里要求的是素数个数的位数,并且这里的n表示的是10^n,其含义是与定理中的x有区别的。
另外,求一个整数x的位数,有公式lg(x) + 1,那么lg(10^n/ln(10^n)) + 1即是本题目所求,在进行简单的化简、编程实现即可。
参考代码如下。
#include<iostream> #include<math.h> using namespace std; int main() { int n; double e = 2.71828; while(cin >> n) { double m = (n - log10(n)-log10(log(10))); cout << int(m) + 1 << endl; } }
除了素数的分布规律,对于判定一个数是否是素数也是一个最基础的问题。
对于素数的判定,我们最先想到的是根据其定义进行暴力穷举。即给定数字n,我们遍历一下[1,n]的整数,判断有可以整除的因子。
但是我们发现,n的因子是成对出现的,即n = i * j,当我们遍历到i的时候,其实是找到了一个因子对——i,j,那么这样我们遍历j的时候,再次访问了因子对——i,j,这就造成了时间上的浪费。从数轴上来看,这些成对的因子是“成对”的,而这个对称点显然是sqrt(n)。因此我们可以对上面判断素数的方法进行优化,遍历[1,sqrt(n)]。
但是还有更高效的算法——埃拉托色尼筛法。它不需要证明,很易懂。就是我们假定[1,N]上的所有整数是素数,然后从2开始往后遍历,如果当前的i是一个素数,那么进入循环,循环中把[1,N]中所有i的倍数筛选出来,标记为合数。对比前两种方法,这种方法显然高效了许多。
以上的方法处理数据的上限是依次递增的,但如果一个数据练第三种筛法都处理不了呢?那我们就灵活的结合第二种普通筛法和第三种高效筛法。假设给定了一个很大的整数n,我们遍历[1,sqrt(n)]间的整数,这里用到的是第二种普通筛法。但是我们只需要遍历这个区间的素数,因为如果是合数的话,它一定有一个更小的素因子,这在之前就一定会遍历到,因此造成了重复遍历引起了时间上的浪费。而如何找到这个区间上的素数,就靠高效的埃拉托色尼筛法了。
只要充分理解了筛法本身的原理,编程实现上就是简单的模拟,很容易实现。
那么我们来结合一个题目具体实现以下代码。(Problem source : nefu 109)
可以看到这就是我们提及到的处理数据非常大的题目,此时就需要两种筛法结合起来。
参考代码如下。
#include<stdio.h> #include<iostream> #include<cmath> #include<cstring> const int N = 50001; using namespace std; bool isprime[N]; int prime[N],nprime; void doprime() //埃拉托色尼筛选法 { long long i , j; nprime = 0; memset(isprime,true,sizeof(isprime)); isprime[1] = 0; for(i = 2;i < N;i++) { if(isprime[i]) { prime[++nprime] = i; for(j = i+i;j < N ;j += i) { isprime[j] = false; } } } } bool isp(int n) //基本筛法 { int i , k = (int)sqrt(double(n)); for(i = 1;prime[i] <= k;i++) if(n%prime[i] == 0) return 0; return 1; } int main() { doprime(); long long n; while(cin >> n) { if(n == 1) { cout << "NO"<<endl; continue; } if(isp(n)) cout << "YES" << endl; else cout << "NO" << endl; } return 0; }
基于我们曾经学过的埃及筛选素数的方法,我们再来探讨是否存在优化埃及筛法的可能性。
在数论中,我们知道这样一个原理——任何一个合数可以拆分成素数乘积的形式,因此我们可以通过这一点,在埃及筛法的基础上优化遍历的数,来实现算法的优化。即可归纳出如下步骤:
step1:找到素数i。
step2:构造出合数i*i。
step3:利用埃及筛法的思想通过+i处理筛掉合数。(i*i + ki一定存在素因子i,因此必为合数。)
step4:向下遍历,重复step1、2、3.值得注意的是,既然我们找的是素数,因此穷举范围就可以缩小到奇数,这样穷举的量就砍掉了一半,这是基于埃及筛法进行优化的精髓所在。 通过编程实现优化后的程序(基于上面的步骤很好实现,代码将会在下面具体的题目中给出),我们与原始的埃及筛法进行耗时的比较,有如下两图。


通过控制两个算法的参数的一致,我们可以看到优化后的算法耗时大约是原始算法的一半。
那么我们开始结合一个具体的题目来应用优化后的算法。(Problem source : hdu 1431)
数理分析:其实对于素数的问题,主要的矛盾点就在于素数的大小,如何不断的优化算法和数据使程序符合评测系统的要求使我们思考的重点。
对于这个问题,更是体现了优化的重要性。
优化1:在素数一些结合别的形式的数的问题中,常常出现筛选所有素数耗时大而判断另一种形式耗时小的情况,这里的“别的形式”就是回文数(还有一些质方数什么的新的定义),我们可以采取的一个基本的方法就是通过耗时较小的那种形式来限定另一种形式。
优化2:我们容易看到11的整数倍是偶位数的回文数,因此我们打表的范围再次缩减,即奇数位的数,基于题目中数据上限是九位数,我们需要打表来找到7位的回文素数,如果没有,再是5位、3位依次往下。 基于上面两个优化分析,我们通过打表处理,得到了7位最大回文素数——9989899。
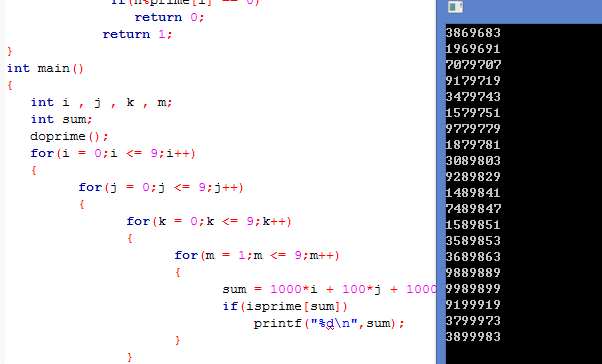
这就完成了上文中我们所描述的优化1,即通过回文数这个限制条件把素数筛选的范围缩小了很多。
基于上述的优化我们便可以编程实现了。
参考代码如下。
#include<stdio.h> #include<iostream> #include<cmath> #include<cstring> const int N = 9989899; using namespace std; bool isprime[N]; int prime[N]; int nprime; int Pprime[N]; void newway() //高效判断素数法:所有合数都等于N个素数的乘积 { int i,j; /*for(i=5;i<=3163;i++) is[i]=0; 由于bool类型默认值是false,所以可以注释掉*/ i=2; for(j=i*i;j<=9989899;j+=i) isprime[j]=true; for(i=3;i<=3163;i=i+2) { if(isprime[i]) continue; for(j=i*i;j<=9989899;j+=i) isprime[j]=true; } } bool test(int a)//判断a是不是回文数 { int temp=a; int b=0; while(temp!=0) { b=b*10; b+=temp%10; temp/=10; } return a==b; } int main() { int a , b; int i; int k = 0; newway(); return 0; for(i = 5;i <= 9989899 ;i++) { if(test(i) && !isprime[i]) { prime[k++] = i; //printf("%d\n",prime[i]); } } while(scanf("%d%d",&a,&b) != EOF) { for(i = 0;i < k;i++) { if(prime[i] < a) continue; else if(prime[i] > b) break; else printf("%d\n",prime[i]); } printf("\n"); } }
从素数的角度来分析整个数域,数学家发现了很多规律,通过归纳法我们很容易得知n可以表示成素数之积,即n = p1*p2*p3……pn,这里的pi是素数。下面我们给出算术基本定理。
定理:每个大于1的正整数n,都可以被唯一地写成素数的乘积:n = p1^a1 * p2^a2 * …… * pk^ak。基于这个式子,我们可以得到很多有用的性质,在文章的后面我们将依次得介绍。
性质1:n!的素因子分解中的素数p的幂为:[n/p] + [n/p^2] + [n/p^3]……。在这里由于时间原因和笔者的能力原因,我们暂且不提它的详尽证明。而是通过先通过实践来学会应用它。
那么让我们来看一道需要应用到这条性质的问题。(Problem source : nefu 118)

我们来看这个问题,显然我们直接求出n!的值而后%10计算的暴力方法是不合理的,我们要灵巧的利用我们刚才得知的性质。因为这条性质中和这道题目一样,都包含n!。我们从素数基本定理的角度来看n!这个数,它可以写成多个素数的乘积的形式,即n! = p1^a1 * p2^a2 * p3^a3…… * pm ^ am的形式。那么此时我们想要知道这个数末尾有多少个零,转化一下,就是通过将n!写成乘积的形式,然后找到10这个因子的幂次,而10又可以继续拆分成两个素数——2和5,即n! = 2^a * 5^b *……,min(a,b)就这这道题目的答案。我们很容易看到,n!这个数字,拆成素数相乘的形式,2的幂次肯定大于5的幂次,因此这里我们只要找到5的幂次,即可作为这道题的答案。
有了这层数理的分析,我们就可以应用到上面的性质了。而在编程实现上,也只需简单的设计循环节来求解即可。
参考代码如下。
#include<cstdlib> #include<iostream> using namespace std; int main() { int n,m,t,sum,five; cin>>n; while(n--) { cin>>m; t = m; five = 5; sum = 0; while(five <= t) { sum = sum + t/five; five = five * 5; } cout << sum << endl; } return 0; }
基于上文给出的算术基本定理及性质1,我们再来看一道引用到这条性质的问题。(Problem source : nefu 119)
Description
小明的爸爸从外面旅游回来给她带来了一个礼物,小明高兴地跑回自己的房间,拆开一看是一个很大棋盘(非常大),小明有所失望。
不过没过几天发现了大棋盘的好玩之处。从起点(0,0)走到终点(n,n)的非降路径数是C(2n,n),现在小明随机取出1个素数p, 他想知道C(2n,n)恰好被p整除多少次?
小明想了很长时间都没想出来,现在想请你帮助小明解决这个问题,对于你来说应该不难吧!
Input
有多组测试数据。 第一行是一个正整数T,表示测试数据的组数。接下来每组2个数分别是n和p的值,这里1<=n,p<=1000000000。
Output
对于每组测试数据,输出一行,给出C(2n,n)被素数p整除的次数,当整除不了的时候,次数为0。
数理分析:可以看到,基于n这样的取值范围,我们通过模拟计算C(2n,n)显然是不切实际的。我们通过组合数公式将其展开——(2n)! / (n! * n!),
这里出现了n!的形式,就往上述给出的性质1的形式靠拢了很多了。
我们可以通过性质1来分别找到2n!和n!根据算术基本定理分解后素因子p的幂次x和y,那么根据2n!和n!在分数线的上下位置,我们很容易得到最终的结果即是x - 2y。
而在具体操作的过程中,只需根据性质将x和y分别求出而后带入整理即可。
有了上述数理分析,编程实现只需简单地设置循环计算即可。
参考代码如下。
#include<cstdlib> #include<iostream> #include<math.h> using namespace std; int main() { int t , n , p , q , sum , tag; double s = 0.0; cin >> t; while(t--) { cin >> n >> p; sum = 0; s = log10(2.0*n)/log10(p); q = (int)s; tag = 1; for(int i = 1;i <= q;i++) { tag = tag*p; sum = sum + (int)(2*n/tag) - 2*(int)(n/tag); } cout << sum << endl; } return 0; }
我们再看一道有关算术基本定理的问题。(Problem source : hdu 2608)
Problem Description
Solving problem is a interesting thing. Yifenfei like to slove different problem,because he think it is a way let him more intelligent. But as we know,yifenfei is weak in math. When he come up against a difficult math problem, he always try to get a hand. Now the problem is coming! Let we
define T(n) as the sum of all numbers which are positive integers can divied n. and S(n) = T(1) + T(2) + T(3)…..+T(n).
Input
The first line of the input contains an integer T which means the number of test cases. Then T lines follow, each line consists of only one positive integers n. You may assume the integer will not exceed 2^31.
Output
For each test case, you should output one lines of one integer S(n) %2. So you may see the answer is always 0 or 1 .
题目大意:T(n)表示数字n的因子和,S=∑T(i) ,其i∈[1,n],现在请你求解S(n) % 2的结果。
数理分析:其实通过题设对两个函数的简单定义,我们能够通过暴力枚举的方法求解,但是那种解题过程太过丑陋,我们思考从数论的角度找到优化的解决方案。
我们利用取余的基本性质,先来分析T(n)%2的结果,显然T(n)这种形式我们并不能分析出什么,我们需要借助一些定理将这个函数进一步转化以方便我们的分析。
考虑到算术基本定理是对整数n的一种转化,我们可以以此为突破口。
n = ∑pi ^ ei,由此我们不难借助生成函数构造出T(n)的另一种形式。
T(n) = ∏∑pi^i 其中i∈[0,ei],由此我们在考察(∑pi^i) %2的情况,2作为唯一一个既是偶数又是素数的整数,而这里又是对2进行取模,所系我们能够看到这里需要针对pi 是够为2进行特殊的讨论。
如果pi为2,容易看到(∑2^i) %2 ≡ 1。
否则,在ei为偶数时,(∑pi^i) % 2 = 1 ;在ei为奇数,(∑pi^i) % 2 = 0。
而我们注意到T(n)基于一种相乘形式,因此当且仅当对于任意的i(pi != 2),ei都是偶数的时候,T(n) = 1。而这一充要条件可以继续进行等价转化,即n = x^2 或者n = 2*x^2。
基于这种算法优化,我们即可通过线性O(n)的时间复杂度下求出S(n)。
参考代码如下。
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int main() { int tt; int a[1005]; int dp[1005]; int num[1005]; scanf("%d",&tt); while(tt--) { memset(dp , 0 , sizeof(dp)); memset(num , 0 , sizeof(num)); int n; scanf("%d",&n); for(int i = 1;i <= n;i++) scanf("%d",&a[i]); dp[1] =1; num[1] = 1; for(int i = 2;i <= n;i++) { int Max1 = 0; for(int j = i - 1;j >= 1;j--) { if(a[i] > a[j]) Max1 = max(Max1 , dp[j]); } dp[i] = Max1 + 1; for(int j = i - 1;j >= 1;j--) { if(dp[j] == Max1 && a[i] > a[j]) num[i] += num[j]; } } int sum = 0; int Max = 0; for(int i = 1;i <= n;i++) Max = max(Max , dp[i]); for(int i = 1;i <= n;i++) if(dp[i] == Max) sum += num[i]; printf("%d\n",sum); } }
我们再来看一道关于素数的问题。(Problem source : hdu 1164)
题目大意:给出数字n,让你将其拆分成质因子相乘的形式。
数理分析:由前文中介绍的算术基本定理——任意一个大于1的正整数都可以唯一地写成素数的乘积,这道题正是基于这一条定理,而让我们编程给出这唯一的素数相乘的具体式子。
编程实现:这里用到类似素数检测我们讨论过的穷举算法,稍加修饰即可实现。
参考代码如下。
#include<stdio.h> int main() { __int64 a[100],num,i,n; while(scanf("%I64d",&n)!=EOF) { num=0; for(i=2;i*i<=n;i++) { if(n%i==0) { while(n%i==0) { a[num++]=i; n=n/i; } } } if(n>1) a[num++]=n; for(i=0;i < num;i++) { if(i == 0) printf("%I64d",a[i]); else printf("*%I64d",a[i]); } printf("\n"); } return 0; }
通过上面几个题目,我们其实能够看到一些逻辑关系,算术基本定理作为理论,以它为基础,我们在实际问题中将整数进行质因数分解,而这个过程又需要继续埃及筛法将素数表给找出来。
我们不妨再来看到一道有关这种“算术基本定理-质因数分解-埃及筛法”的题目。(Problem source : hdu 3988)
数理分析:有关整除性的问题,我们第一个需要想到的是将k和n进行质因数分解,因为这将极大的将很大的整数n、k给微小化,然后我们通过积累微小问题的解来得到最终结,这是很多编程思维的一个核心思想。
设k = ∏pi^ek[i] , n! = ∏pi^en[i],则我们应该能够看到,i的最大值其实就是min{en[i]/ek[i] | en[i] ≠ 0 且 ep[i] ≠ 0}。
但是这里我们面临一个问题,对于k的一个素因子pi,我们用试除的方法容易得到ep[i],但是对于n!的一个素因子pi呢,我们如何得到en[i]?
我们需要从特殊的角度来看待除法运算,对于素因子pi,我们通过n / pi能够得到1x2x3......xn中有多少个因子满足能够整除pi,但是这就是ep[i]了么?当然不是,举个例子来说,对于10!的一个素因子2,10/2 = 5,即2、4、6、8、10能够整除2,但是4 = 2x 2,8 = 2x2x2。那么如何才能正确的计算出这些漏掉的情况呢?很简单,我们计算n/p[i]^2、n/p[i]^3......,即算出阶乘因子中p[i]^2的整数倍、p[i]^3的整数倍,很显然,对于某个因子p[i]^j来说,整个计算过程中将会被记录j次,这样便可以不漏的正确计算出ep[i]。
这个题目虽然数据比较庞大,但是通过打[2,10^7]的素数表还是可以过的。由于这个范围的限制,导致k被质因分解之后可能仍然是一个大于10^7的素数,因此利用循环和素数表将k质因数分解后,还需要再做一步运算。
简单的参考代码如下。
#include<iostream> #include<cstdio> const int maxn = 10000000 + 5; using namespace std; bool flag[maxn]; int cnt=0,prime[maxn]; void Init() { for(int i=2;i<=maxn;i++) { if(flag[i]) continue; prime[cnt++]=i; for(int j=2;j*i<=10000000;j++) flag[i*j]=true; } } long long get(long long n,long long p) { long long ret=0; while(n) { n/=p; ret+=n; } return ret; } int main() { int t,tt = 0; scanf("%d",&t); Init(); while(t--) { long long n,k; scanf("%I64d %I64d",&n,&k); if(k==1) { printf("Case %d: inf\n",++tt); continue; } long long imax=-1; for(int i=0;i<cnt&&prime[i]<=k;i++) { if(k%prime[i]==0) { int ek=0; while(k%prime[i]==0) { ek++; k /= prime[i]; } long long en = get(n,prime[i]); long long tmp=en/ek; if(imax==-1) imax=tmp; else imax=min(imax,tmp); } } if(k>1) { long long en= get(n,k); int ek = 1; long long tmp = en/ek; if(imax==-1) imax=tmp; else imax=min(imax,tmp); } printf("Case %d: %I64u\n",++tt,imax); } return 0; }
下面我们探讨一些关于梅森素数的问题。
梅森素数的定义:一个数如果可以表示成2^p - 1,其中p是素数,那么我们称这个数为梅森数。
基于梅森数的定义,我们可以看到,如果p是合数的话,2^p - 1一定是合数。这里用到简单的因式分解技巧可以证明。
我们从2^mn - 1开始。2^mn - 1 = 2^mn - 2^((m-1)n) + 2^((m-2)n) + 2^((m-2)n)……-2^n + 2^n - 1
= 2^((m-1)n)(2^n - 1) + 2^((m-2)n)(2^n - 1)……
=(2^n - 1)(2^((m-1)n) + 2^((m-2)n) + ……)
此时我们就将2^mn - 1拆成了乘积的形式,这就表明在梅森素数的定义中,如果p是合数,那么2^p - 1一定是合数。如果p是素数,那么这个数是梅森数,但是它本身是质数还是合数,却是不确定的。我们举几个例子:2^2 - 1 = 3,是一个素数。2^11 - 1= 23 * 89 = 2047,不是一个素数。 因此如何判断一个梅森数是否是素数,成了数学家感兴趣的课题。 下面我们就介绍两种判断梅森数是否为素数的算法,由于时间和空间所限,这里依然是简单的介绍算法的用法,详细的证明笔者将会在以后的深入学习中给出。
Lucas-Lehmer判断法:我们设第p(p > 2)个梅森数为Mp = 2^p - 1。再令r1 = 4,通过递归式rk = r(k-1)^2 - 1得到一个r的序列,那么当且仅当r(p-1)%Mp = 0的时候,我们可以判定Mp是梅森素数。
基于对此算法的理解,我们先解决一个实际问题来体现以下这种判断法的编程实现。(Problem source : nefu 120)

可以看到,这道题目就是很直白的要你对梅森数进行素数判断,这里的数据2^62虽然用64位整型(__int64)可以处理,但是用前面我们学过的筛法判断还是太慢,所以这里我们用Lucas-Lehmer算法则则会更高效。但值得一提的是,我们生成r序列的时候,指数是2^(2^(2^(2^2……))有60多层,这个数可不是一般的大,我们注意到算法中是需要对Mp取模的,因此可以通过将乘法转化成加法,期间不断取模来处理非常大的数据(加法运算不会对取模结果造成影响),这也是在组合数学、数论中很常用的处理超大数据的方法。
参考代码如下。
#include<cstdlib> #include<iostream> using namespace std; long long multi(long long a , long long b , long long m) //(a*b) % m { long long ret = 0; while(b > 0) { if(b & 1) ret = (ret + a)%m; b >>= 1; //b = b*2 a = (a << 1)% m; // a = a/2; } return ret; } int main() { long long sum = 1 , data[66],temp; int n,p; data[1] = 4; cin>>n; while(n--) { sum = 1; cin >> p; sum <<= p; sum -= 1; //得到第p个梅森数 for(int i = 2;i <= p - 1;i++) { temp = multi(data[i-1],data[i-1],sum); data[i] = (temp - 2)%sum; } if(p == 2) //基于Lucas-Lehmer判断法,p = 2时需要特殊判断 cout << "yes"<<endl; else { if(data[p-1] == 0) cout<< "yes"<<endl; else cout<<"no"<<endl; } } return 0; }
上文中给出了素数、梅森素数的定义以及一些筛选筛法,下面我们给出完全数的定义。
完全数也称完美数,也是数论领域数学家们位置倾倒的美丽数字,如果一个数字m,它的所有真因子(不包括它本身的因子)之和等于m,那么这类数字便叫做完全数。
完全数还有一些很奇妙的性质,在以后深入探讨中我们会一一给出并证明。
根据完全数的定义,我们可以通过计算机编程,来得到它。所谓物以稀为贵,所谓完美数,想梅森素数一样,也是少得可怜,起劲发现的完美数仅有28个。
我们这里给出前10个完美数。
6、28、496、8128、33550336、8589869056、137438691328、2305843008139952128、2658455991569831744654692615953842176、191561842608236107294793378084303638130997321548169216。
知道了完全数的定义,和前10个完全数,我们来尝试做一道题目(Problem source : sdut 1220)
题目描述
输入
输出
数理分析:这里运用简单的打表模拟方法即可轻松实现。
参考代码如下。
#include<cstdio> #include<iostream> using namespace std; int main() { int m , n; int perfect[5] = {6,28,496,8128,33550336}; while(scanf("%d%d",&m,&n) != EOF) { if(n == 0 && m == 0) break; int flag = 1; for(int i = 0;i < 5;i++) { if(perfect[i] >= m && perfect[i] <= n && flag == 1) {printf("%d",perfect[i]);flag = 0;} else if(perfect[i] >= m && perfect[i] <= n && flag == 0) {printf(" %d",perfect[i]);} } if(flag) printf("No"); printf("\n"); } }
在数论当中,将一个整数n表示成多个素数相乘的形式,叫做整数分解,也叫作质因数分解。其实与我们判断一个整数n是否是素数很类似,整数分解也有着逐步优化的算法。
方案1:试除法,遍历[2,n],得到约数,显然当前一定是素因子,然后用n除以该约数直到不能除尽,然后继续遍历。
方案2:试除法,遍历[2,sqrt(n)],得到约数,显然当前一定是素因子,然后用n除以该约数直到不能除尽,然后继续遍历。
方案3:筛选法,遍历[2,sqrt(n)],先得到该范围内的素数,然后再判断是否是约数。
方案4:Pollard rho整数分解法。
我们先来看前三个方案,他们的效率是依次递增的。我们观察方案2、3,我们给定同一个数字n,那么这两种方案在求解的时候的有效步骤是相同的,即记录到素因子的步骤。那么比较二者算法的效率,只需分析他们无效步骤的多少即可。我们在讲视野缩小到每次记录素因子的过程,假设在相邻的两次次计算中,我们会记录下素因子factor[i]、factor[i+],分别对应着第i个素数prime[i]和第j个素数prime[j]。
那么方案2需要至少遍历prime[j] - prime[i]的操作,之所以说最少,是因为在记录下素因子之后,可能还需要让整数n多步连续这个素因子。
而针对方案3,其实只需要遍历prime[i]和prime[j]之间的素数的个数的次数即可,这步优化节约了很多的时间复杂度,并且及时加上了筛法生成素数表的过程,方案3的优势依然很大。
我们通过一道题目来分别实现我们给出的方案2和方案3。(Problem source : hdu 1164)
方案2:
#include<stdio.h> int main() { __int64 a[100],num,i,n; while(scanf("%I64d",&n)!=EOF) { num=0; for(i=2;i*i<=n;i++) { if(n%i==0) { while(n%i==0) { a[num++]=i; n=n/i; } } } if(n>1) a[num++]=n; for(i=0;i < num;i++) { if(i == 0) printf("%I64d",a[i]); else printf("*%I64d",a[i]); } printf("\n"); } return 0; }
方案3:
#include<stdlib.h> #include<stdio.h> #include<iostream> #include<string.h> #include<cmath> const int N = 65536; using namespace std; int prime[N]; int nprime; bool isprime[N]; void make_prime() { int i , j; nprime = 0; memset(isprime , 1 , sizeof(isprime)); isprime[1] = 0; for(i = 2;i <= sqrt (N-1.0);i++) { if(isprime[i]) { nprime++; prime[nprime] = i; for(j = i*i;j < N;j += i) { isprime[j] = 0; } } } } void divide(int n) { int i , ct = 0 , factor[N]; int temp = sqrt(n + 0.0); for(i = 1;i <= nprime;i++) { if(prime[i]>temp) break; while(n%prime[i] == 0) { ct++; factor[ct] = prime[i]; n /= prime[i]; if(ct != 1) printf("*"); printf("%d",prime[i]); } } if(n != 1) { ct++; if(ct != 1) printf("*"); printf("%d",n); factor[ct] = n; } } int main() { int n; make_prime(); while(scanf("%d",&n) != EOF) { divide(n); printf("\n"); } }
参考系:《数论及其应用》 陈宇
——<未完>


 浙公网安备 33010602011771号
浙公网安备 33010602011771号