软件工程第三次作业
1.题目
题目(1):最大连续子数组和(最大子段和)
问题:
给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科》
具体要求:
(1) 请从上述两个题目中根据个人实力任选一题,要求写出可运行的完整代码提交至GitHub或者Coding.net系统中,并将代码地址附到博客内,题目(1)可以参考这篇博文
(2) 请从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖五个覆盖标准中(条件组合覆盖难度较大,鼓励尝试,但请谨慎选择),任选一个标准设计测试用例
(3) 请利用自动测试工具对程序进行测试
(4) 请将程序运行结果和自动测试分析结果截图附到博客中
2.算法分析
运用了动态规划的思想来解决最大子段和问题,通过遍历累加这个数组元素,定时的更新最大子段和,如果当前累加数为负数,直接舍弃,重置为0,然后接着遍历累加。
时间复杂度:O(n)。
3.代码清单
include<iostream>
using namespace std;
int MaxSum(int n, int a[])
{
int sum = 0;
int i = 0;
int max = 0;
for (i = 0; i <n; i++)
{
sum = sum + a[i];
if (sum < 0)
sum = 0;
if (sum >= max)
max = sum;
}
return max;
}
int main()
{
int n = 0;
int a[100];
int maxsum;
while (cin >> a[n])
{
n++;
if (cin.get() == '\n')
break;
}
maxsum = MaxSum(n, a);
cout <<maxsum<<"\n";
system("pause");
return 0;
}
程序代码链接:点这里
4.单元测试
(1)在解决方案上右键添加新建项,选择测试,本机单元测试项目
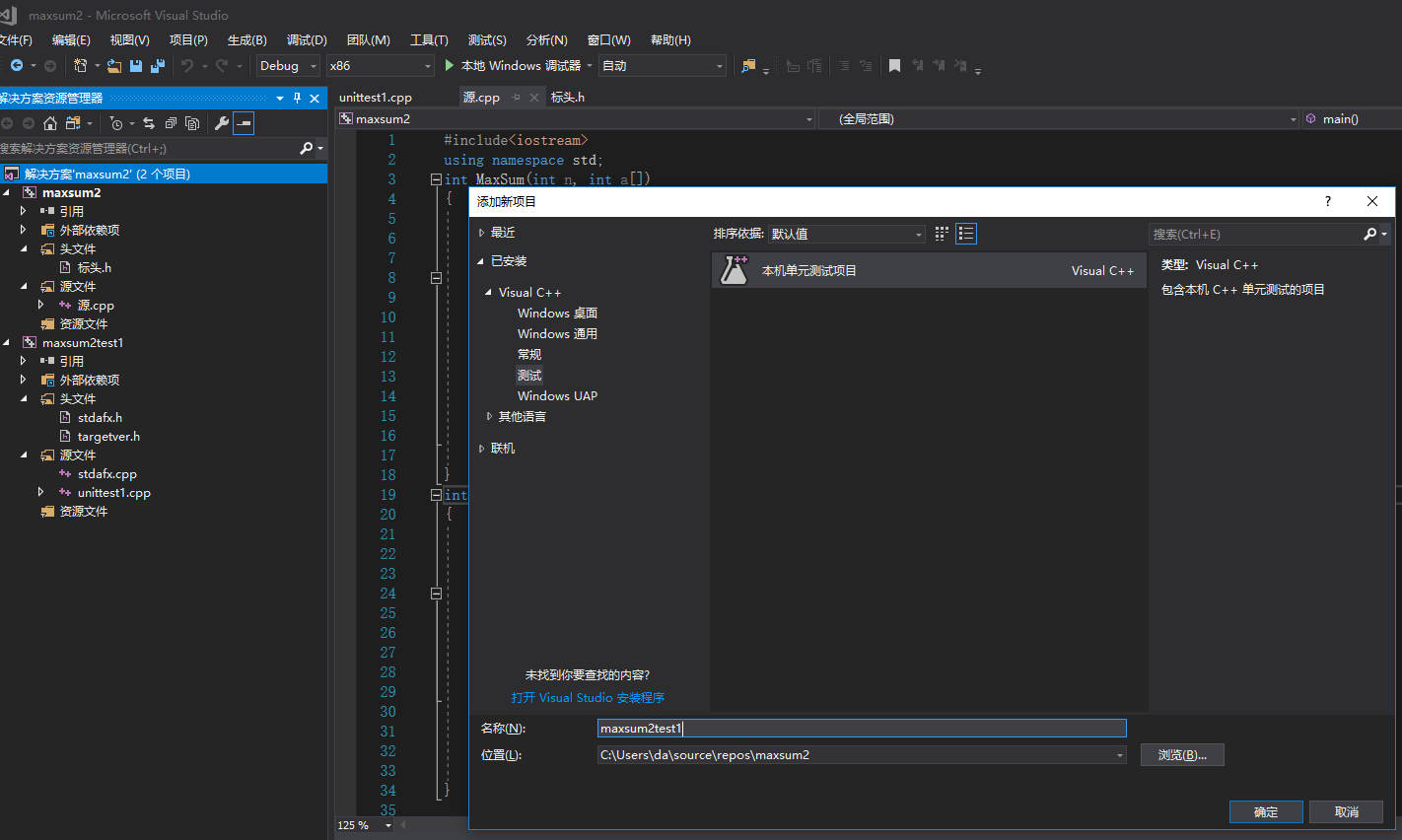
(2)将完成代码复制到测试代码前
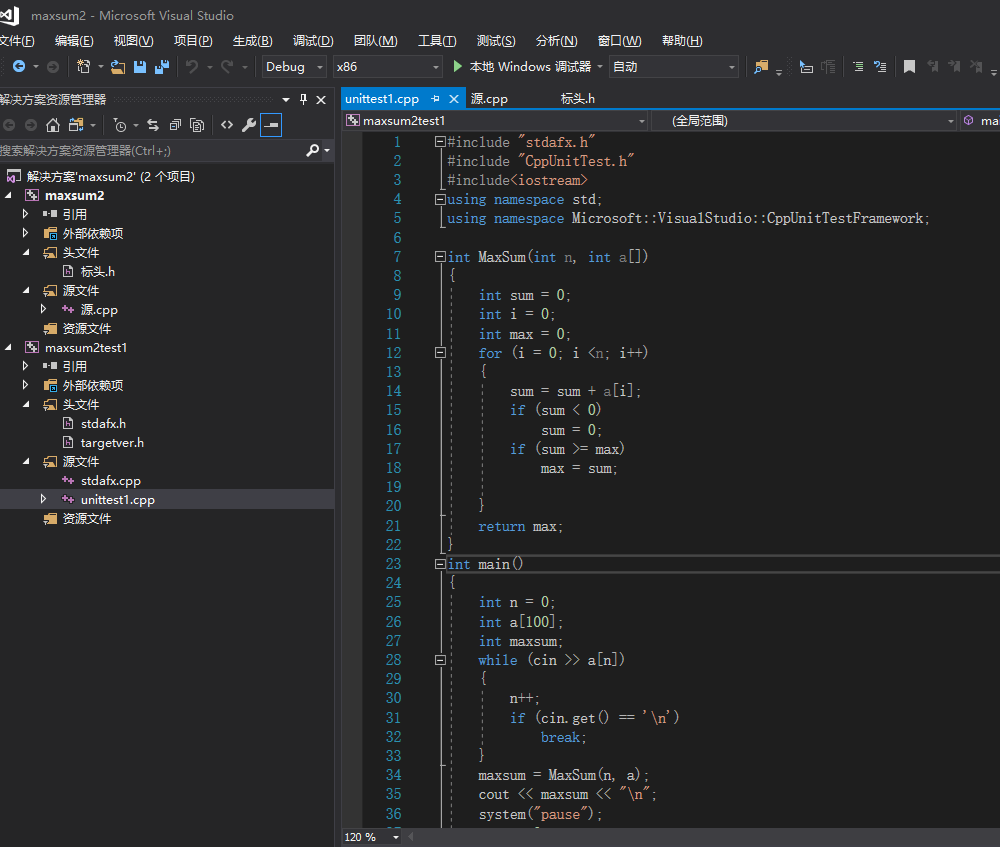
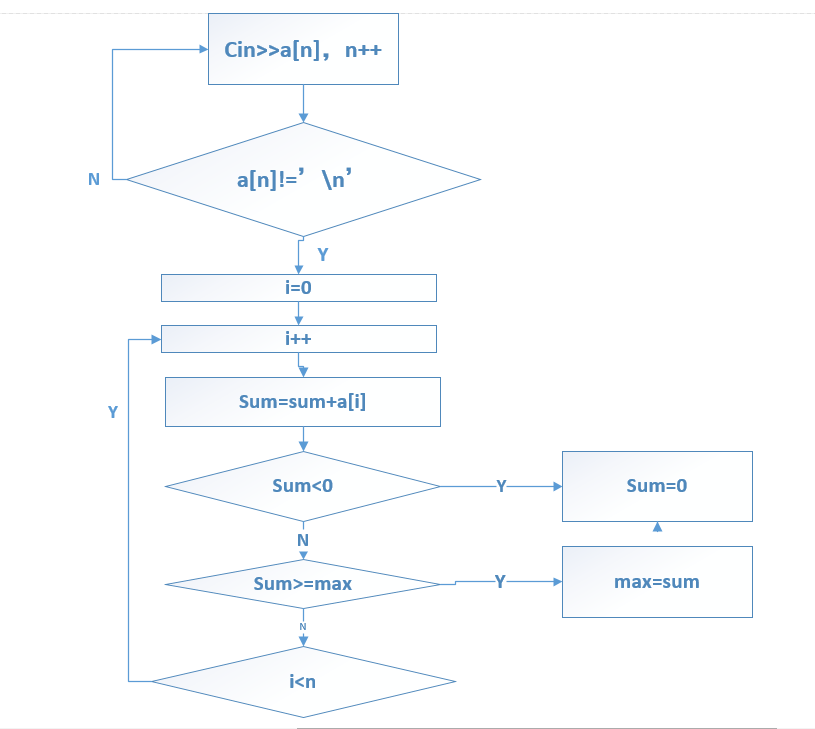
(3)程序流程图如下:
5.覆盖方法的比较与选择
(1)语句覆盖:使得程序中每个语句至少都能被执行一次。
(2)判定覆盖:使得程序中每个判定至少为T和F各一次。
(3)条件覆盖:使得判定中的每个条件获得各种可能的结果。
(4)判定/条件覆盖:同时满足判定覆盖和条件覆盖。
(5)条件组合覆盖:使得每个判定中条件的各种可能组合都至少出现一次。
- 我选择的是条件覆盖:
- 测试用例:
样例1:a[3]={1,2,3}结果maxsum为6
样例2:a[4]={-1,2,-4,2}结果maxsum为2
样例3:a[3]={-1,-2,-3}结果maxsum为0
样例4:a[6]={-2,11,-4,13,-5,-2}结果maxsum为20
- 测试用例:
测试代码清单:
include "stdafx.h"
include "CppUnitTest.h"
include<iostream>
using namespace std;
using namespace Microsoft::VisualStudio::CppUnitTestFramework;
int MaxSum(int n, int a[])
{
int sum = 0;
int i = 0;
int max = 0;
for (i = 0; i <n; i++)
{
sum = sum + a[i];
if (sum < 0)
sum = 0;
if (sum >= max)
max = sum;
}
return max;
}
int main()
{
int n = 0;
int a[100];
int maxsum;
while (cin >> a[n])
{
n++;
if (cin.get() == '\n')
break;
}
maxsum = MaxSum(n, a);
cout << maxsum << "\n";
system("pause");
return 0;
}
namespace maxsum2test1
{
TEST_CLASS(UnitTest1)
{
public:
TEST_METHOD(TestMethod1)
{
int a[3] = { 1,2,3 };
int n = 3;
int maxsum =MaxSum(n, a);
Assert::AreEqual(6, maxsum);
}
TEST_METHOD(TestMethod2)
{
int a[4] = {-1,2,-4,2 };
int n = 4;
int maxsum = MaxSum(n, a);
Assert::AreEqual(2, maxsum);
}
TEST_METHOD(TestMethod3)
{
int a[3] = { -1,-2,-3 };
int n = 3;
int maxsum = MaxSum(n, a);
Assert::AreEqual(0, maxsum);
}
TEST_METHOD(TestMethod4)
{
int a[6] = { -2,11,-4,13,-5,-2 };
int n = 6;
int maxsum = MaxSum(n, a);
Assert::AreEqual(20, maxsum);
}
};
}
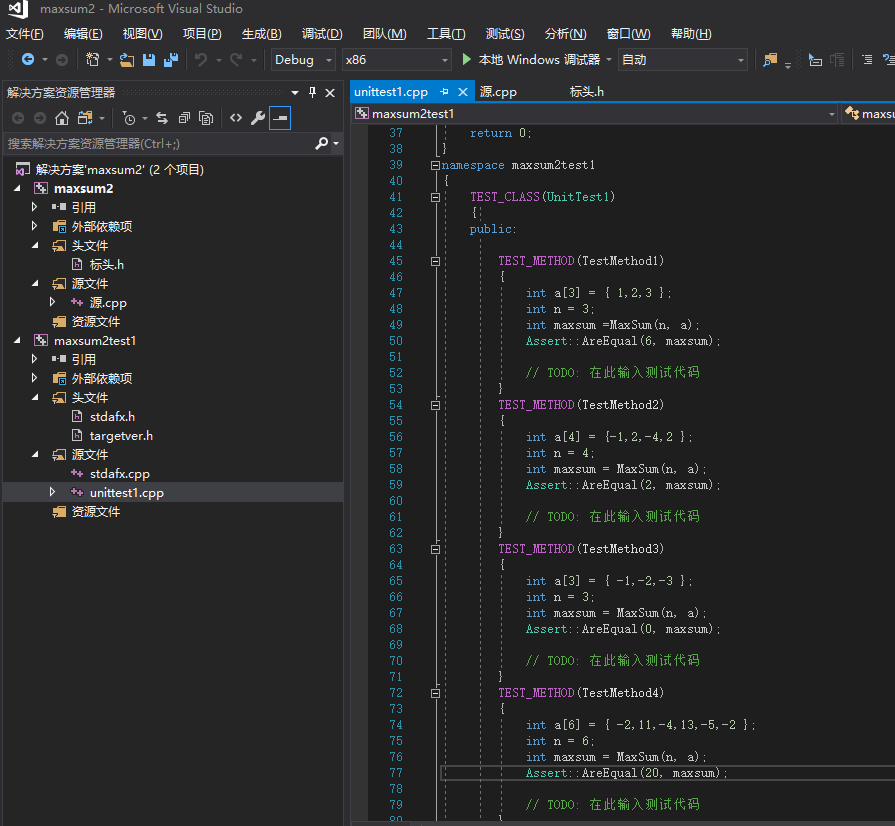
- 运行单元测试:通过
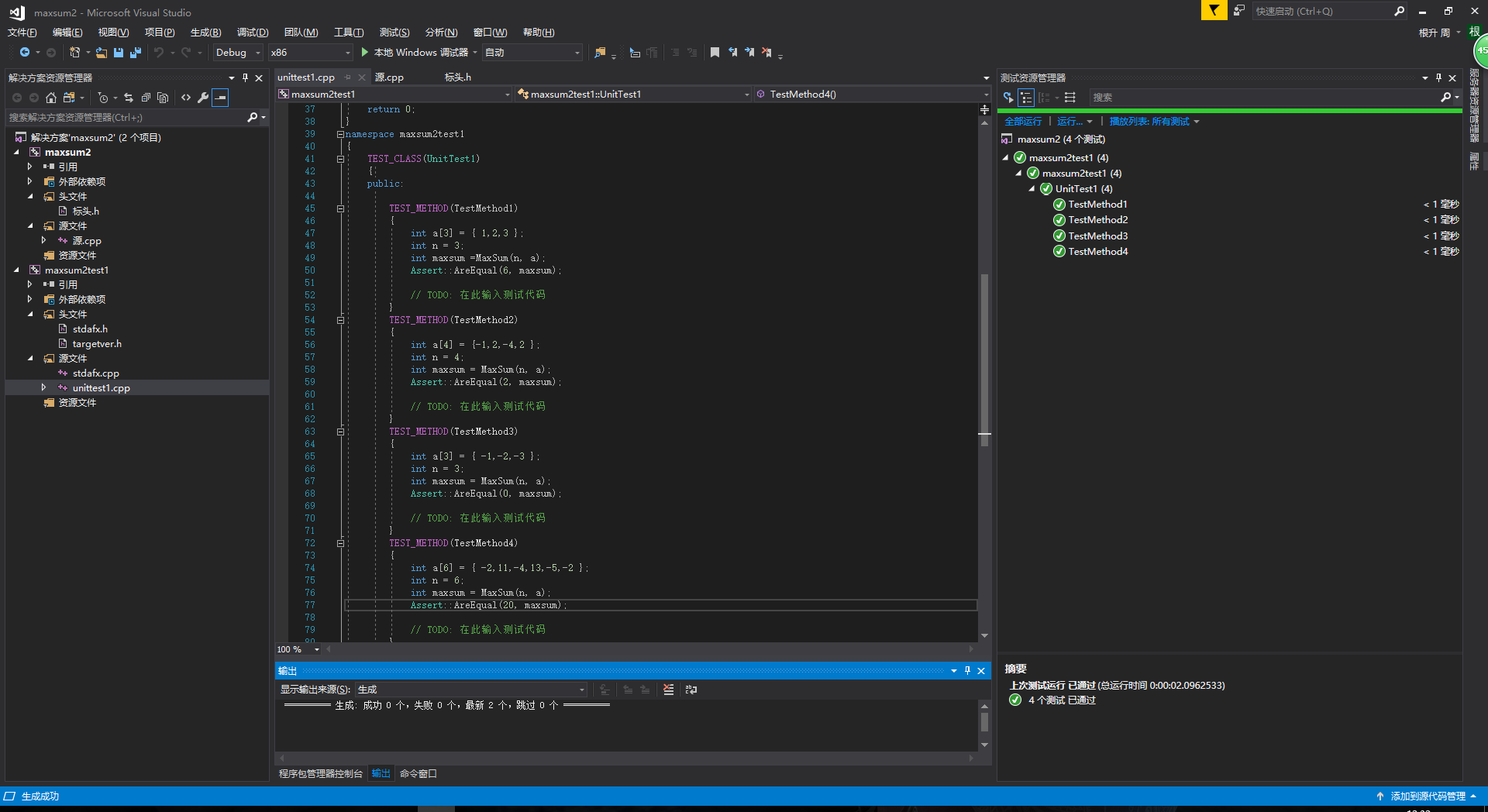
6.总结感悟
在看到第三次作业时,求最大连续子数组和(最大子段和)。我自己没有想到什么快捷的算法来编写程序,于是上网百度了一下问题,我用了几天的时间好好弄懂了什么是动态规划的思想。通过这次作业,我感觉收获颇多,首先掌握了动态规划思想,其次我更明白了在想完成一个程序前更应该做好知识储备和上网学习 ,在做好相应的准备后,编写程序就事倍功半了。





