k-Nearest Neighbors algorithm

在开始kNN博文之前，举一个小栗子。当手中的杯子突然滑落，从一米多高的空中坠向地板，常人会惊慌失措，心想：坏了，要碎了！这一下意识的想法，恰恰说明了kNN运作的机理：没有人在此之前见过那只特定的杯子打碎的样子， 但是大家见过很多其他杯子打碎的样子，以及很多杯子虽然摔落但没有碎掉的例子。所以我们知道，在相似的情况下，杯子十有八九是保不住了！

 

如下图所示的问题：已经两类红色圆圈和绿色方块，及其分布，要预测蓝色星星的分类。

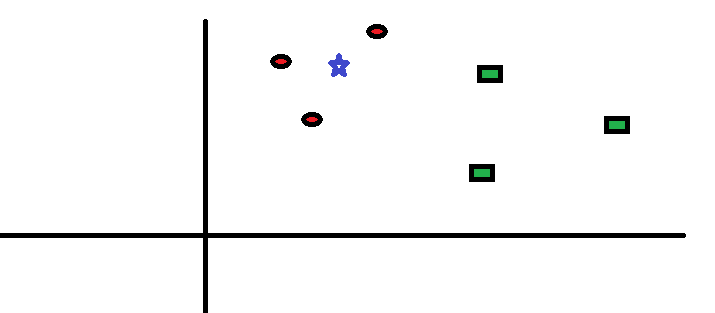
kNN的工作原理非常简单：选择距离自己最近的k个邻居点，然后进行投票（即选择邻居点中大多数所属的类别）。

 

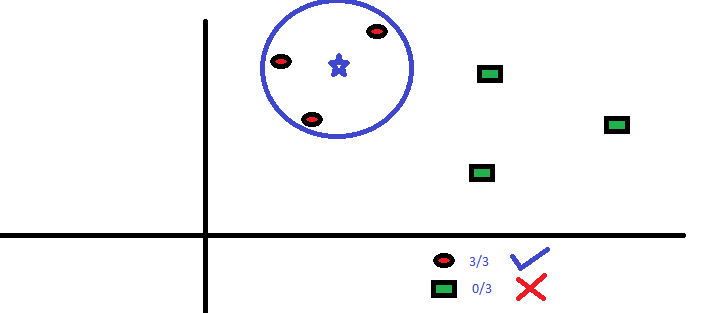
如我标红加粗的两个关键词一样，kNN运作良好的两个前提条件是：对距离的定义，以及邻居个数k的选择。常用的距离计算公式为，Euclidean Distance：

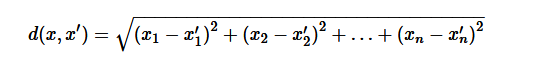
此外还有：Manhattan, Chebyshev and Hamming distance等。

 

再来说说k的选择，一如在Regularization中选择lambda是一样，k值选择过小容易过拟合(Overfitting)，而k值选择过大容易欠拟合(Underfitting)。如下图，注意decision boundary的不同：

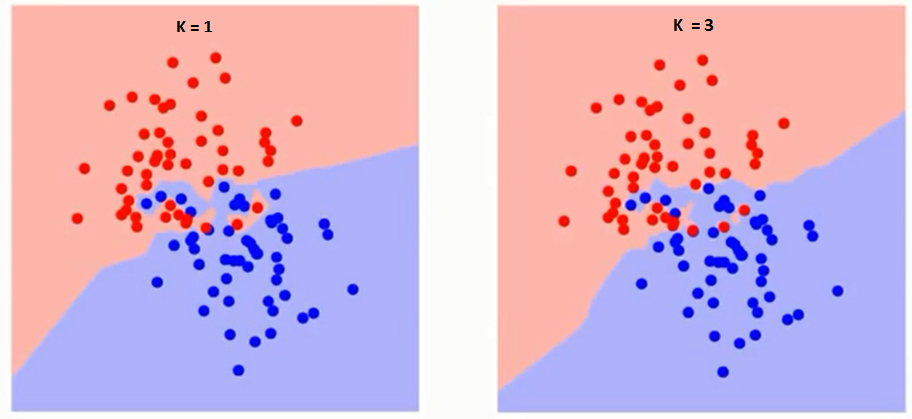
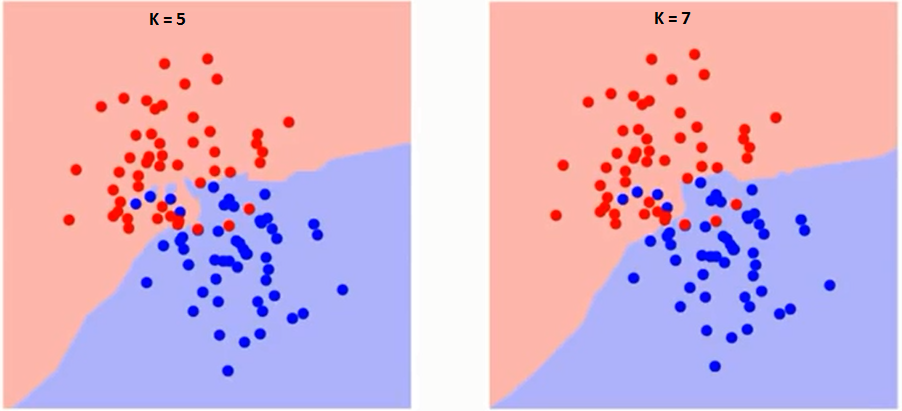
将数据集分割为training set和validation set，取其trade-off的k值，从下面两张图的曲线中，我们即可得出K=10是本例中的一个不错选择。

 

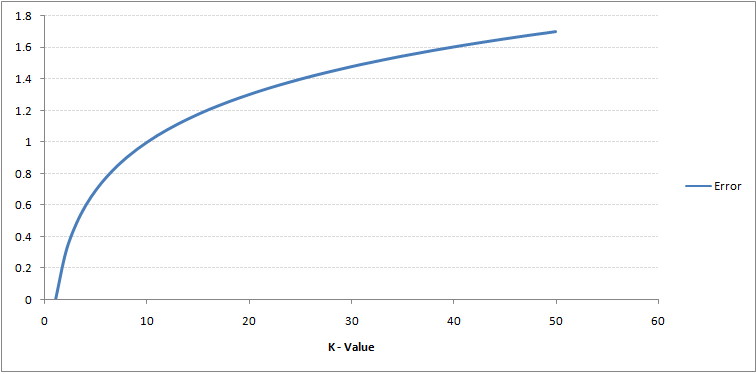
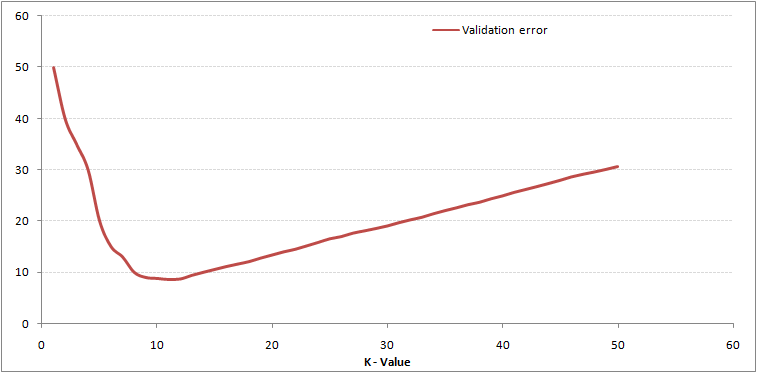
再啰嗦两句：kNN属于所谓的lazy algorithm(lazy learning)，即学习过程不是在做prediction之前提前进行的，而是在query时进行运算。优点来了，kNN不用去学习任何model，也就不用受限于任何model。因为很多模型是有假设条件的，比如training set要服从高斯分布，等等。问题也来了，其运算速度受限于training set的大小，因为要计算target example与所有examples的距离从而选取最近的k个。

 

kNN的原理就是如此简单，所以说，不仅仅只有神经网络在模仿人脑工作过程，kNN也在以类似人脑推理的方式运作着。回到最初的例子，在那样的高度，材质是玻璃杯，地板是硬的，我们建立起了一个三维坐标轴，根据以往那些碎了和没碎的例子，我们得出分类的结果：必碎无疑！