【读书笔记】:MIT线性代数(5):Four fundamental subspaces
At the beginning, the difference between rank and dimension: rank is a property for matrix, while dimension for subspaces. So we can obtain the rank of A, which reveals dimensions of four subspaces(2 from A, 2 from AT).

Important fact: The row space and column space have the same dimension r (the rank of the matrix). N(A) and N(AT) have dimensions n - rand m - r, to make up thefull nand m. C(A) and C(R) are different subspaces, because row operations reserve row spaces, but change column spaces.
Four subspaces:

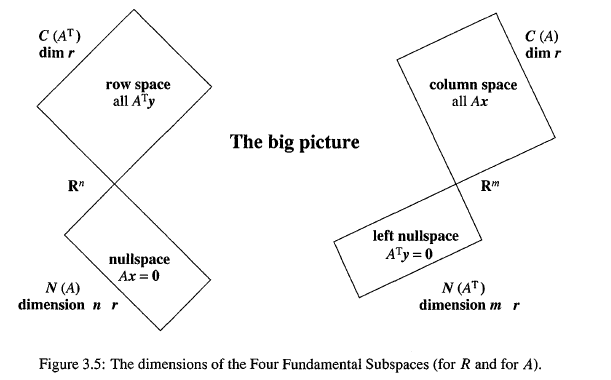
Illustration:Notice the relationships between A and R:
1. The row space of R has dimension two, matching the rank. The first two row span the space, and the third row contributes nothing. The pivot rows are independent, so they are a basis for the row space.
A has the same row space as R. Same dimension r and same basis. Row operations don't change row space, because every row in of A is a combination of R.
2. The column space of R has dimension r=2. The number of independent rows is equal to the number of independent columns.The pivot columns are basis of C(R), and they span the column space.
C(A) has dimension r=2. However, C(A)≠C(R)! The same combinations of the columns are zero (or nonzero) for A and R. Say that another way: Ax = 0 exactly when Rx = 0.
3. The null space of R has the dimension n-r. Apart from pivot columns, there are n-r free variables,giving us n-r special solutions. The combination of them span the null space of R. And the special solutions are a basis of R. The fact is: To generate zero by column combinations, we must set pivot columns always equals zero, then combine free variable columns linearly to span the null space.
A has the same nullspace as R. Same dimension n - r and same basis. Reason: The elimination steps don't change the solutions.
4. The nul space of RT has dimension m-r, it is to generate zero by row combinations. As well, the pivot rows need to be zero, then we have m-r free variable rows. The reason for the name "left nullspace" is that RTy = 0 can be transposed to yTR = 0T.
The left nullspace of A has dimension m - r.



