【读书笔记】：MIT线性代数(4):Independence, Basis and Dimension

Independence:

The columns of A are independent when the nullspace N (A) contains only the zero vector.

Example1:

1. If three vectors are not in the same plane, they are independent. No combination of V₁, V_2, V₃ in Figure 3.4 gives zero except 0V₁ + 0V₂ + 0V₃.
2. If three vectors W₁, W₂, W₃ are in the same plane, they are dependent.

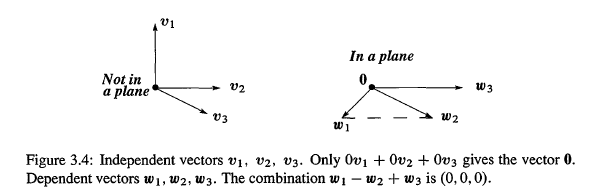
Example2:

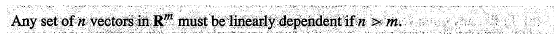
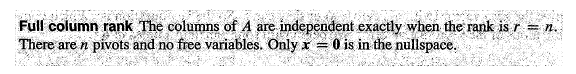
 Vectors that Span a Subspace:

 

A basis of a vector space:

Every vector v in the space is a combination of the basis vectors, because they span the space.There is one and only one way to write v as a combination of the basis vectors.

 

Dimension:

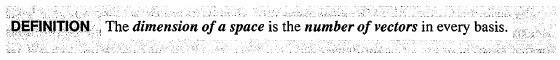
The dimension of C(A) is the rank of matrix A. The dimension of N(A) is the number of free variables(n-r)!