【读书笔记】：MIT线性代数(2):Vector Spaces and Subspaces

Vector Space:

R¹, R², R³,R⁴ , .... Each space Rⁿ consists of a whole collection of vectors. R⁵ contains all column vectors with five components. This is called "5-dimensional space". The great thing about linear algebra is that it deals easily with five-dimensional space. We don't draw the vectors, we just need the five numbers (or n numbers).

 

A real vector space is a set of "vectors" together with rules for vector addition and for multiplication by real numbers. The addition and the multiplication must produce vectors that are in the space.

xy plane is a typical R² space, consists of all the 2-D vectors. If the origin point were removed, this would not be a vector space again. Because if the scalar multiplier is zero, the produced vector will not in that space. Every vector space has the origin point.

 

The commutative law is v + w = w + v;  the distributive law is c(v + w) = cv + cwo ; There is a unique "zero vector" satisfying 0 + v = v.

 

Subspace:

Fact:Every subspace contains the zero vector

Example1: Sub space of R²:

a. Zero point; b. Line in R² going through zero point; c.R² itself

Example2: Sub space of R³:

a. Zero point; b. Line in R³ going through zero point; c. Plane in R³ going through zero point; d.R³ itself

 

Column space of A:

Start with the columns of A, and take all their linear combinations. This produces the column space of A. It is a vector space made up of column vectors.C (A) contains not just the n columns of A, but all their combinations Ax.

To solve Ax = b is to express b as a combination of the columns. The right side b has to be in the column space produced by A on the left side, or no solution!

Suppose A is an m by n matrix. Its columns have m components (not n). So the columns belong to R^m. The column space of A is a subspace of R^m (not Rⁿ).

Example1:

Example2: C(I) is R², C(A) is a line in R², C(B) is R²

 

Null Space of A: Solving Ax=0

One solution is x=0, for invertible matrix A, it's the only solution; for other matrices, there are nonzero solutions, each of them belongs to Null Space.

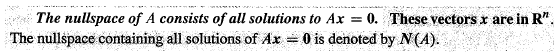
The solution vectors x have n components. They are vectors in Rⁿ, so the nullspace is a subspace of Rⁿ. The column space C (A) is a subspace of R^m. If the right side b is not zero, the solutions of Ax = b do not form a subspace. The vector x = 0 is only a solution if b = 0. When the set of solutions does not include x = 0, it cannot be a subspace.