Parameter Initializations in Deep Learning
全零初始化的问题:
在Linear Regression中,常用的参数初始化方式是全零,因为在做Gradient Descent的时候,各个参数会在输入的各个分量维度上各自更新。更新公式为:

而在Neural Network(Deep Learning)中,当我们将所有的parameters做全零初始化,根据公式:

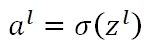
可知,每一层的Zl均为0,如果使用sigmoid activation,则al的值都等于0.5。在反向传播时,误差值
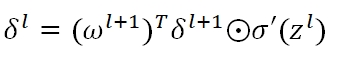
因为有ω在里面,所以导致δ都变成了零,而我们用于做Gradient Descent的梯度
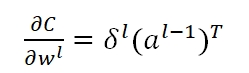
也就通通变为了零,从而,我们的Back propagation算法失效,参数矩阵将始终保持全零的状态,无法更新。
Parameter初始化过小的问题:
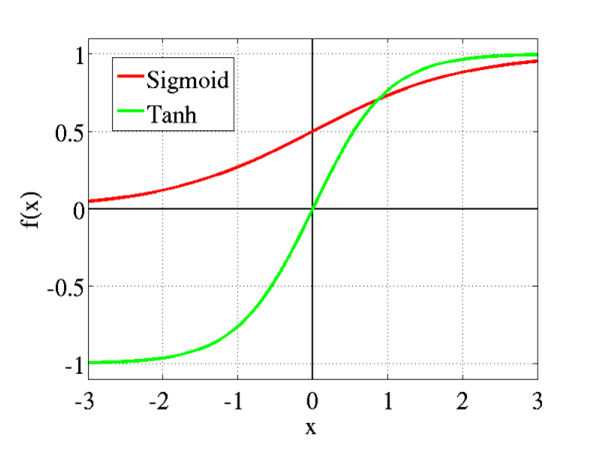
首先,Parameter过小,则经过一层层的Sigmoid Function,activation会越来越小,也就是最终的输出结果会非常接近于0。从Sigmoid的图形可以看出,在接近0的图形范围内,函数是类似线性的。所以Parameter初始化过小,会导致神经网络失去非线性功能。此外,在接近0点的部分,Sigmoid Activation的δ'(z)接近于1/4。同样地,在公式中:
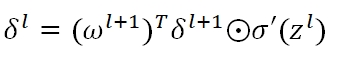
随着Backpropagation的进行,δ指数级衰减。下式中的梯度会随着层数的回溯,越来越小,直至消失消失。
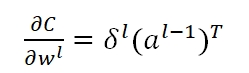
Parameter初始化过大的问题:
将导致Z值过大,从Sigmoid和Tanh图形可知,当Z值过大时,激励函数会饱和,其梯度将趋近为0。导致的结果是,参数将无法进行更新,或更新很慢。
而如果我们通过调整bias,使得各层的z始终为0,则会有梯度爆炸的问题。还是在下式中
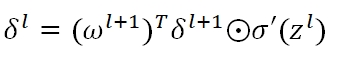
各层的δ‘(z)都是1/4,但ω却是很大的值。所以随着Backpropagation的推进,前层的δ会越来越大,如果层数很多,甚至变为NAN。
深度学习中的主流初始化方法有Xavier和He
Xavier Initialization有三种选择,Fan_in:

Fan_out:
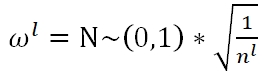
Average:
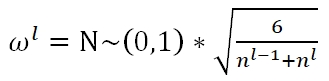
He Initialization:
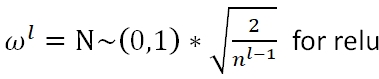
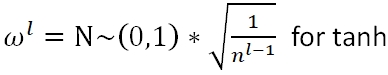



 浙公网安备 33010602011771号
浙公网安备 33010602011771号