Recurrent Neural Network(2):BPTT and Long-term Dependencies

在RNN(1)中，我们将带有Reccurent Connection的node依照时间维度展开成了如下的形式：

 

在每个时刻t=0,1,2,3,...，神经网络的输出都会产生error：E₀,E₁,E₂,E₃,....。同Feedforward Neural Network一样，RNN也使用Backpropagation来更新参数V,W,U，只不过对于RNN，该算法称为Backpropagation Through Time(BPTT)。其算法思路为：根据各个时刻的输出（如果有），计算各个时刻的Loss Function(Error)，而后对各个时刻的loss求和。如果使用mini-batch，则再对batch内的examples求和，计算Cost Function。而后分别对V,W,U求梯度，最后最梯度下降。

 

在本例中，我们设定从某个时刻的状态s_t，到最终的输出，一路经过：与权重V相乘得到输出值o_t;转换为Softmax输出概率;Cost Function使用Cross-entropy，得到t时刻的误差值E_t。基于此设定，我们来看该误差在V上的梯度：

 

可以看出，t时刻所产生误差，在V上的梯度，只与当前时刻的状态与输出有关。下面再来看E_t在W上的梯度：

在上式中，s_t的计算公式为:

其中f(z)是activation function，而s_t-1也是w的函数，所以在求梯度时不能简单视其为常量。经过推导后得出：

上式是误差在各个时间分量上的梯度之和，可以看出，某个时间t上的误差E_t,会延时间方向反向传播(Backpropagation Through Time)，如下图：

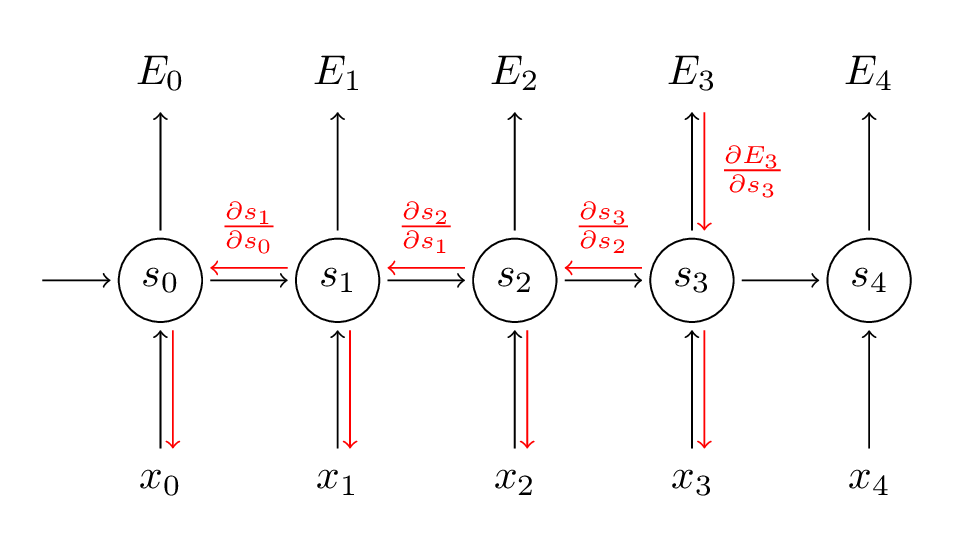
而上式中的，dS_t/dS_k本身就是链式法则，我们展开后可以得到类似Feedforward NN里Gradient Vanishing Problemactivation function偏导数连程形式。据此可以知晓，虽然E_t在W上的梯度是求和的形式，看似考虑了该误差与所有时间t之间的关系，实际上该误差随着t维度上深度的增加逐渐衰减。而在参数U上面，同样也存在了此Gradient Vanishing的问题。

 

从而，我们的RNN模型无法获取到Long term dependencies. 例如：The country I traveled with my wife Mia in 2013 summer holiday is Japan ,这里需要填写的词是一个国家的名字。GRU和LSTM会解决此问题。