Gradient Vanishing Problem in Deep Learning

在所有依靠Gradient Descent和Backpropagation算法来学习的Neural Network中，普遍都会存在Gradient Vanishing Problem。Backpropagation的运作过程是，根据Cost Function进行反向传播，利用Chain Rule去计算n层之前某一weight上的梯度，从而更新该weight。而事实上，在网络层次较深的情况下，我们获得的weight梯度，随着反向传播层次的深入，会呈现越来越小的状态。从而，在靠近输出端的Layers中，weight可以被很好的更新，因为可以获得不错的gradient，而在靠近输入端的Layers中，weight则更新缓慢。

 

举个最简单的例子，来说明该问题。如下的神经网络有四层，每层有一个node：

 

 

我们可知w是weight，b是bias，每一层的节点输入是z，输出是a，activation function是a=σ(z)，我们可以得出：

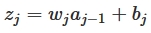
当我们已知Cost Function时，我们利用Backpropagation计算weight:

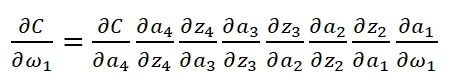
可以看到，第一层的weight梯度，依赖于之后各层activation function的一阶导数之积。而对于Machine Learning中常用的Sigmoid及tanh激励函数，其derivative图像如下：

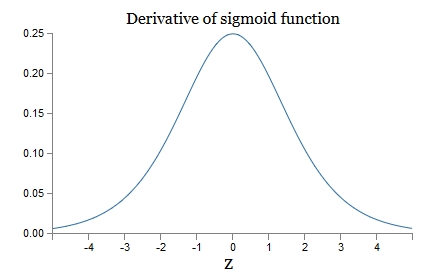
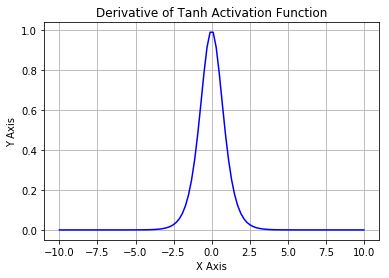
Sigmoid的derivative是[0,0.25]的，而tanh的derivative是[0,1]的。通过上式，我们看出，通过Backpropagation求梯度时，每往回传播一层，就要多乘以一项δ‘(z)，也就是说，随着向回传递的深入，梯度会呈指数级的衰减，直至缩减到0，导致前层的权重无法更新。tanh要略好于sigmoid，但依然难以解决Gradient Vanishing的问题。所以Relu Function应运而生，并且在Deep Learning方面取得了巨大成功。Relu的表达式及图形如下：

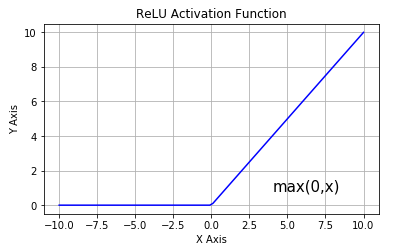
其当x>0时，derivative是1，小于0时，derivative为0。该函数很好的解决了Gradient Vanishing Problem，在大多数情况下，我们构建Deep Learning时可以使用Relu作为默认的Activation Function。