[Paper Review]Distilling the Knowledge in a Neural Network,2015

Analogy: Many insects have a larval form that is optimized for extracting energy and nutrients from the environment and a completely different adult form that is optimized for the very different requirements of travelling and reproduction.
The problem in Machine Learning: In large-scale machine learning,
we typically use very similar models for the training stage and the
deployment stage despite their very different requirements: For tasks
like speech and object recognition, training must extract structure from
very large, highly redundant datasets but it does not need to operate
in real time and it can use a huge amount of computation. Deployment to a
large number of users, however, has much more stringent requirements on
latency and computational resources.
What is the knowledge in Neural Network?
A conceptual block that may have prevented more investigation of this
very promising approach is that we tend to identify the knowledge in a
trained model with the learned parameter values and this makes it hard
to see how we can change the form of the model but keep the same
knowledge. A more abstract view of the knowledge, that frees it from any
particular instantiation, is that it is a learned mapping from input
vectors to output vectors.
Why knowledge transfer?
For tasks like MNIST in which the cumbersome model almost always
produces the correct answer with very high confidence, much of the
information about the learned function resides in the ratios of very
small probabilities in the soft targets. For example, one version of a 2
may be given a probability of 10−6 of being a 3 and 10−9 of being a 7
whereas for another version it may be the other way around. This is
valuable information that defines a rich similarity structure over the
data (i. e. it says which 2’s look like 3’s and which look like 7’s) but
it has very little influence on the cross-entropy cost function during
the transfer stage because the probabilities are so close to zero.
Simple transfer: An obvious way to transfer the generalization
ability of the cumbersome model to a small model is to use the class
probabilities produced by the cumbersome model as “soft targets” for
training the small model.
Redefine the Softmax Function:
A term called Temperature T is added into Softmax Function as following.
The larger the T is, the smoother the result probability matrix will
be.
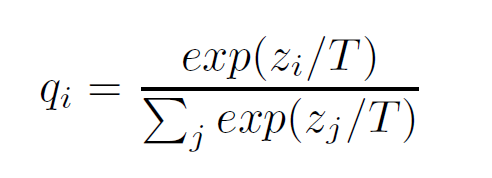
Distillation:
In the simplest form of distillation, knowledge is transferred to the distilled model by training it on a transfer set and using a soft target distribution for each case in the transfer set that is produced by using the cumbersome model with a high temperature in its softmax. The same high temperature is used when training the distilled model, but after it has been trained it uses a temperature of 1.
https://arxiv.org/pdf/1503.02531.pdf


 浙公网安备 33010602011771号
浙公网安备 33010602011771号