State Function Approximation: Linear Function
In the previous posts, we use different techniques to build and keep updating State-Action tables. But it is impossible to do the same thing when the number of states and actions get huge. So this post we gonna discuss about using a parameterized function to approximate the value function.
Basic Idea of State Function Approximation
Instead of looking up on a State-Action table, we build a black box with weights inside it. Just tell the blackbox whose value functions we want, and then it will calculate and output the value. The weights can be learned by data, which is a typical supervised learning problem.
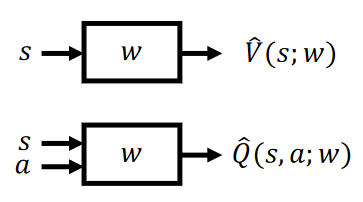
The input of the system is actually the feature of state S, so we need to do Feature Engineering (Feature Extraction) to represent the state S. X(s) is the feature vectore of state S.

Linear Function Approximation with an Oracle
For the black box, we can use different models. In this post, we use Linear Function: inner product of features and weights
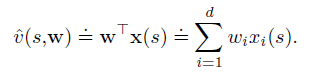
Assume we are cheatingnow, knowing the true value of the State Value function, then we can do Gradient Descent using Mean Square Error:
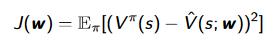
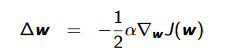
and SGD sample the gradient:
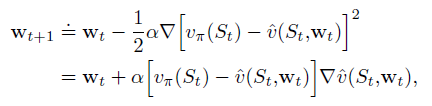
Model-Free Value Function Approximation
Then we go back to reality, realizing the oracle does not help us, which means the only method we can count on is Model-Free algorithm. So we firstly use Monte Carlo, modifying the SGD equation to the following form:

We can also use TD(0) Learning, the Cost Function is:

the gradient is:
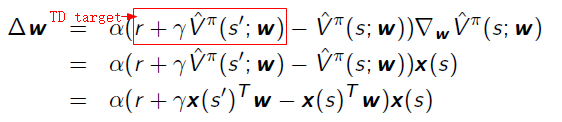
The algorithm can be described as:

Model-Free Control Based on State-Action Value Function Approximation
Same as state value function approximation, we extract features from our target problem, building a feature vector:
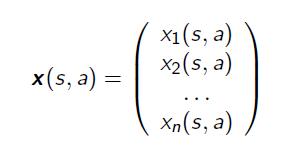
Then the linear estimation for the Q-function is :
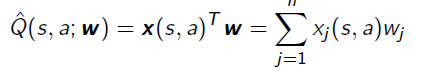
To minimize the MSE cost function, we can get Monte Carlo gradient by taking derivative:
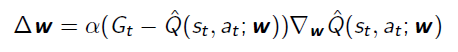
SARSA gradient:
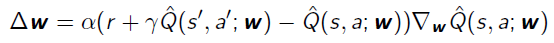
Q-Learning gradient:
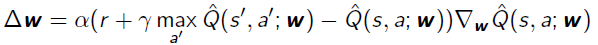
References:
https://www.youtube.com/watch?v=buptHUzDKcE
https://www.youtube.com/watch?v=UoPei5o4fps&list=PLqYmG7hTraZDM-OYHWgPebj2MfCFzFObQ&index=6


 浙公网安备 33010602011771号
浙公网安备 33010602011771号