Monte Carlo Control
Problem of State-Value Function
Similar as Policy Iteration in Model-Based Learning, Generalized Policy Iteration will be used in Monte Carlo Control. In Policy Iteration, we keep doing Policy Evaluation and Policy Improvement untill our policy converging to Optimal Policy.

Every time when we improve the policy, the action that gives the best return(reward+value function of the next state) will be picked.
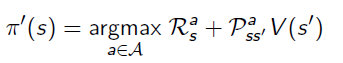
The problem of this algorithm if we directly transfering to Monte Carlo is: it is based on the Transition Matrix.
Monte Carlo Control based on Q function
The idea of Policy Iteration can be used to Estimite Action-Value Function, and it is very useful for Model-Free problem. The process of choosing actions does not depend on State-Value function, because the return from a specific action is given by Monte Carlo estimation.

Q function can be updated by:
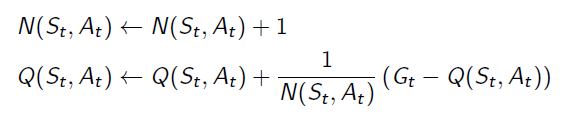
When we improve the policy, we just pick the action that produce the maximum Q value.
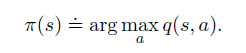
Exploration-exploitation Dilemma and ε-Greedy Exploration:
In Model-Based Policy Iteration algorithm, we update all State-Value function within a single policy evaluation process, so that we can choose the best actions from the whole action space whiled improving policies. Nevertheless, Monte Carlo Learning only updates the Action-Value functions whose actions were taken on the previous episode. So there are probabily some actions having better returns than the actions we have tried. Sometimes we need to give them a trial. We call that problem the Exploration-Exploitation Delemma.
It is necessary to try some new opened restaurant, rather than going to the usual place every day.
ε-Greedy Exploration is the algorithm that gives the agent probability=ε to choose randomly actions and 1-ε to stay on the optimal action.
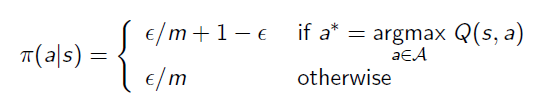


 浙公网安备 33010602011771号
浙公网安备 33010602011771号