Temporal-Difference Learning for Prediction

In Monte Carlo Learning, we've got the estimation of value function:

 

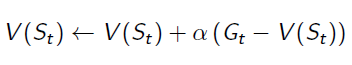
G_t is the episode return from time t, which can be calculated by:

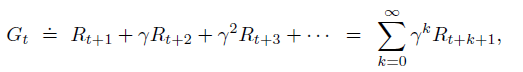
Please recall, G_t can be only calculated at the end of a given episode. This reveals a disadvantage of Monte Carlo Learning: have to wait until the end of episodes.

 

TD(0) algorithm replace G_t of the equation to the immediate reward and estimated value function of the next state:

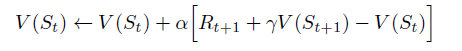
The algorithm updates the Estimated State-Value Function at time t+1, because everything in the equation is determined. This means we will wait until the agent reaching the next state, so that the agent can get the immediate reward R_t+1 and know which state the system will transition to at time t+1.

 

The equations below are State-Value Function for Dynamic Programming, in which the whole environment is known. Compare to these equations:

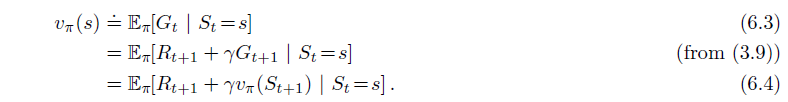
TD algorithm is quite like 6.4 Bellman Equation, but it does not take expectation. Instead, it uses the knowledge till now to estimate how much reward I am going to get from this state. The whole algorithm can be demonstrated as:

 

TD Target, TD Error

Bias/ Viriance trade-off

Bootstraping