Optimal Value Functions and Optimal Policy

Optimal Value Function is how much reward the best policy can get from a state s, which is the best senario given state s. It can be defined as:

 

Value Function and Optimal State-Value Function

Let's see firstly compare Value Function with Optimal Value Function. For example, in the student study case, the value function for the blue circle state under 50:50 policy is 7.4.

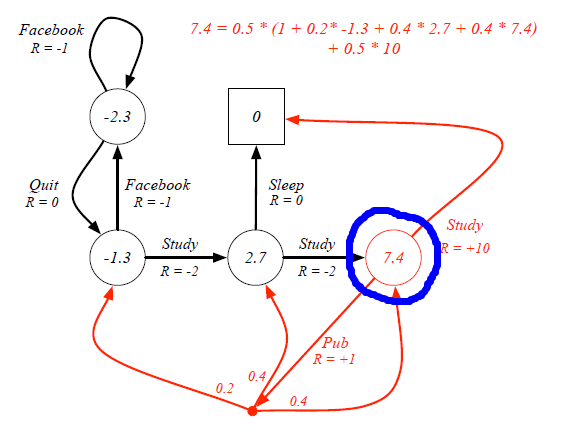
However, when we consider the Optimal State-Value function, 'branches' that may prevent us from getting the best scores are proned. For instance, the optimal senario for the blue circle state is having 100% probability to continue his study rather than going to pub.

 

Optimal Action-Value Function

Then we move to Action-Value Function, and the following equation also reveals the Optimal Action-Value Function is from the policy who gives the best Action Returns. 

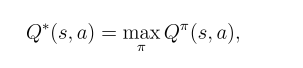
The Optimal Action-Value Function is strongly related to Optimal State-Value Function by:

 

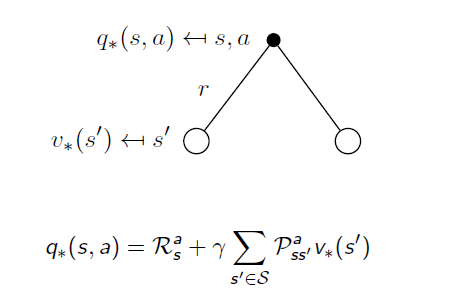
The equation means when action a is taken at state s, what the best return is. At this condition, the probability of reaching each state and the immediate reward is determined, so the only variable is the State-Value function . Therefore it is obvious that obtaining the Optimal State-Value function is equivalent to holding the Optimal Action-Value Function.

 

Conversely, the Optimal State-Value function is the best combination of Action and the following states with Optimal State-value Functions:

Still in the student example, when we know the Optimal State-Value Function, the Optimal Action-Value Function can be calculated as:

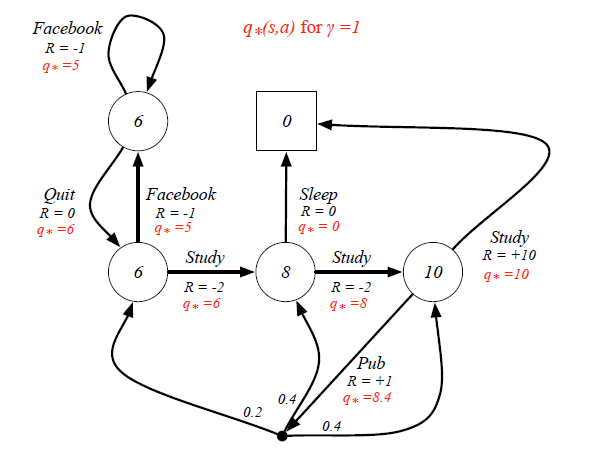
Finally we can derive the best policy from the Optimal Action-Value Function:

 

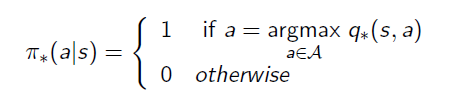
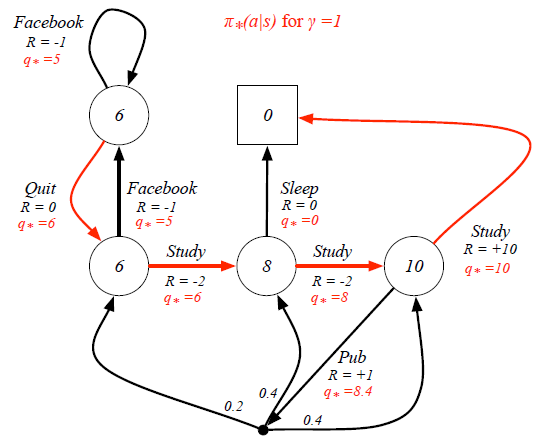
This means the policy only picks up the best action at every state rather than having a probability distribution. This deterministic policy is the goal of Reinforcement Learning, as it will guide the action to complete the task.