02 基础篇

二分查找

编写二分查找代码：
1.前提：有已排序的数组A
2.定义左边界L、有边界R、确定搜索范围，循环执行二分查找（3、4两步）
3.获取中间索引M=Floor((L+R)/2)（向下取整）
4.中间索引的值A[M]与待搜索值T进行比较
1. A[M]==T表示找到，返回中间索引
2. A[M]>T,中间值右侧的其他元素都大于T,无需比较，中间索引左边去找，M-1设置为有边界，重构内心查找
3. A[M<T,中间值左侧的其他元素都小于T,无需比较，中间索引右边去找，M+1设置为左边界，重新查找
5.当L>R时，表示没有找到，应结束循环

int array = {1,3,4,5,6,7,8,9};
int target = 7;
int idx = binarySearch(array,target);
System.out.println(idx);

//二分查找
public static int binarySearch(int[] a, int t){
	int l = 0,r = a.length-1,m;
	while(l<=r){
		//可能出现的问题：l+r可能会溢出
		m=(l+r)/2; //l/2 + r/2 ===> l+(-l/2+r/2)====>l+(r-l)/2  或(l+r)>>>1
		if(a[m]==t){
			return m;
		}else if(a[m]>t){
			r = m-1;
		}else{
			l = m+1;
		}
	}
	return -1;
}

例题：

答案：4 4 2的几次方时多少是128 即log2 128 取整+1
解题思路：
奇数二分取中间
偶数二分取中间靠左

注意：此例是以Arrays.binarySearch的实现做参考

排序

掌握（快排、冒泡、选择、插入）实现思路，手写冒泡、快排代码，了解各个排序算法的特性，时间复杂度是否稳定。

冒泡排序

1.一次比较数组中相邻两个元素大小，若a[j]>a[j+1]则交换两个元素，两两都比较一遍称为一轮冒泡，结果是让最大的元素排至最后
2.重复以上步骤，直到整个数组有序
3.优化方式：每轮冒泡时，最后一次交换索引可以作为下一轮冒泡的比较次数，如果这个值为零，表示整个数组有序，直接退出外层循环即可

public static void main(String[] args){
	int[] a = {4,2,3,6,12,4,21,354};
	bubble(a);
}
public static void bubble(int[] a){
//如果其中有一轮冒泡没有交换
	boolean swapped = false;
	for(int j=0;j<a.length-1;j++){
		//一轮冒泡
		for(int i=0;i<a.length-1-j;i++){
			if(a[i]>a[i+1]){
				swap(a,i,i+1);
				swapped = true;
			}
		}
		if(!swapped){
			break;
		}
	}

}
public static void swap(int[] a,int i,int j){
	int t = a[i];
	a[i] = a[j];
	a[j] = t;
}

//优化
public static void main(String[] args){
	int[] a = {4,2,3,6,12,4,21,354};
	bubble(a);
}
public static void bubble(int[] a){
	int n = a.length -1;
//如果其中有一轮冒泡没有交换
	while(true){
		//一轮冒泡
		int last = 0;//表示最后一次交换索引位置
		for(int i=0;i<n;i++){
			if(a[i]>a[i+1]){
				swap(a,i,i+1);
				last = i;
			}
		}
		n = last;
		if(n==0){
			break;
		}
	}

}
public static void swap(int[] a,int i,int j){
	int t = a[i];
	a[i] = a[j];
	a[j] = t;
}

选择排序

1.将数组分为两个子集，排序的和未排序的，每一轮从未排序的子集选出最小的元素，放入排序子集
2.重复以上步骤，直到整个数组有序
3.优化方式：减少交换次数，每一轮可以先找到最小索引，在每轮最后再交换元素

int[] a = {5,3,7,2,1,9,8,4};
selection(a);
private static void selection(int[] a){
	for(int i=0;i<a.length-1;i++){
		//i 代表每轮选择的最小元素要交换的目标索引
		int s = i;//代表最小的索引
		for(int j=s+1;j<a.length;j++){
			if(a[s] > a[j]){
				s = j;
			}
		}
		if(s!=i){
			swap(a,s,i);
		}
	}
}
public static void swap(int[] a,int i,int j){
	int t = a[i];
	a[i] = a[j];
	a[j] = t;
}

插入排序

1.将数组分为两个区域，排序区域和未排序区域，每一轮存未排序区域去除第一个元素，插入到排序区域（保存顺序）
2.重复以上步骤，知道整个数组有序
3.优化方式：待插入元素进行比较时，遇到了比自己小的元素，就代表找到了插入位置 ，无需再进行插入

int[] a = {9,3,7,2,5,8,1,4};
insert(a);
System.out.println(Arrays.toString(a));

public static void insert(int[] a){
	//i:代表插入元素的索引
	for(int i=1;i<a.length;i++){
		int t = a[i];//代表待插入的元素值
		int j = i-1;//代表已排序的区域的元素索引
		while(j>=0){
			if(t < a[j]){
				a[j+1] = a[j];
			}else{
				break;//退出循环，减少比较的次序
			}
			j--;
		}
		a[j+1] = t;
	}
}

希尔排序（增加一个间隙，对插入排序进行优化）

习题：

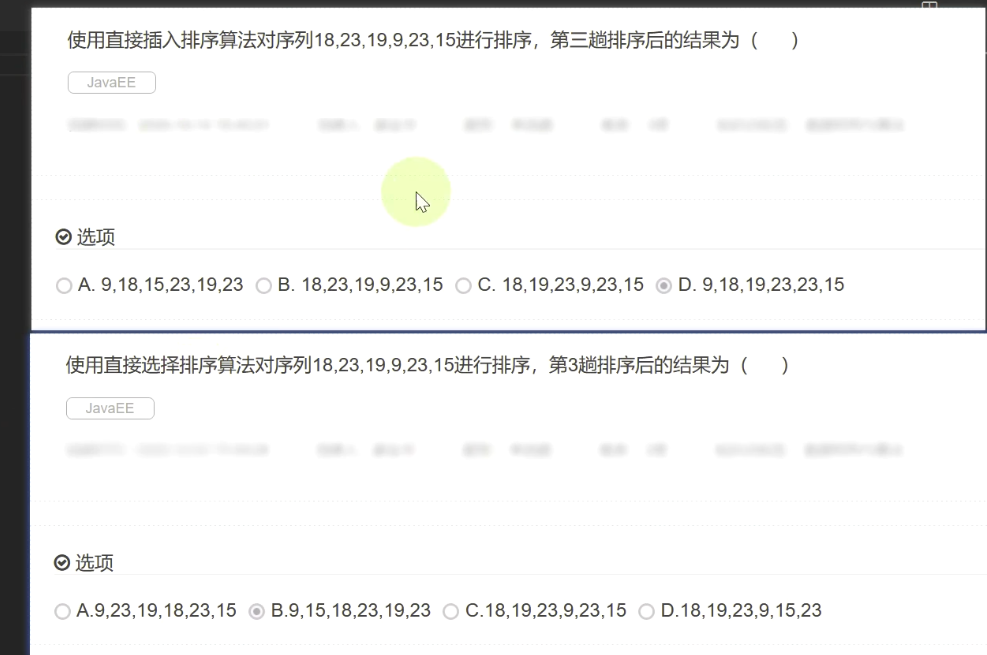
答案：D B

快速排序

1.每一轮排序选择一个基准点（pivot）进行分区。让小于基准点的元素进入一个分区，大于基准点的元素的进入另一个分区。当分区完成时，基准点元素的位置就是其最终位置
2.在子分区内重复以上过程，知道子分区个数少于等于1，这体现的是分而治之的思想（devide-and-conquer)

单边循环快排

1. 选择最右元素作为基准点元素
2. j指针负责找到比基准点小的元素，一旦找到则于i进行交换
3. i指针维护小于基准点元素的边界，也是每次交换的目标索引
4. 最后基准点于i交换，i即为分区位置

	public static void main(String[] args){
		int[] a = {6,3,2,56,7,8,12}
		quick(a,0,a.length-1);
	}
	public static void quick(int[] a,int l,int h){
		if(l>=h){
			return;
		}
		int p = partition(a,l,h);//p 索引值
		quick(a,l,p-1);
		quick(a,p+1,h);
	}
	private static int partition(int[] a,int l,int h){
		//返回值代表基准点元素所在的正确索引，用它确定下一轮分区的边界
		int pv = a[h];//基准点元素
		int i = l;
		for(int j = l;j<h;j++){
			if(a[j]<pv){
				if(i!=j){
					swap(a,i,j);
				}
				i++;
			}
		}
		if(i!=h){
			swap(a,h,i);
		}
		return i;
	}

双边循环快排

1. 选择最左边元素作为基准点元素
2. j指针负责从右往左找比基准点小得元素，i指针负责从左向右找比基准点大得元素，一旦找到二者交换，直至i，j相交
3. 最后基准点于i（此时i与j相等）交换，i即为分区位置

public static int partition(int[] a,int l,int h){
	int pv = a[l];
	int i = l;
	int j = h;
	while(i<j){
		//j从右边找比基准点小的元素
		while(i<j&&a[j]>pv){
			j--;
		}
		//i从左找大的
		while(i<j&&a[i]<= pv){
			i++;
		}
		swap(a,i,j);
	}
	swap(a,l,j);
	return j;
}

面试题：ArrayList

ArrayList()会使用长度为零的数组
ArrayList(int initialCapacity)会使用指定容量的数组
public ArrayList(Collection<? extends E> c)会使用c的大小作为数组容量
add(Object o)首次扩容为10，在此扩容为上次容量的1.5倍
addAll(Collect c)没有元素时，扩容为Math.max(10,实际元素个数)，有元素时为Math.max(原容量1.5倍，实际元素个数)

面试题：fail-fast和fail-safe

fail-fast:一旦发现遍历的同时其它人来修改，则立刻抛出异常(ArrayList)
fail-safe 返现遍历的同时其他人来修改，应当能有应对策略：读写分离，例如：牺牲一致性，来让整个遍历运行完成（CopyOnWriteArrayList)

LinkedList 和ArrayList

ArrayList:
1.基于数组，需要连续内存
2.随机访问快（指根据下标放温）
3.尾部插入、删除性能可以，其他部分插入、删除都会移动数据，因此性能会低
4.可以利用cpu缓存，局部性原理
LinkedList:
1.基于双向链表，无需连续内存
2.随机访问慢（要沿着链表遍历）
3.头尾插入删除性能高
4.占用内存多

HashMap

底层结构，1.7和1.8有何不同？ 1.7 数组+链表 1.8 数组+（链表|红黑树）
为何要用红黑树，为何一上来不树化，树化阈值为何是8，何时会树化，何时会退化为链表？
1.红黑树用来避免DOS攻击，防止链表超长时性能下降，树化应当是偶然情况
1. hash表的查找，更新的时间复杂度是O(1),而红黑树的查找，更新的时间复杂度是O(log2n),TreeNode占用空间也比普通Node的大，如非必要，尽量还是使用链表
2. hash指如果足够随机，则在hash表中给你按泊松分布，在负载因子0.75的情况下，当都超过8的链表出现概率是0.00000006,选择8就是为了让树化几率足够小
2.树化的两个条件：链表长度超过树华阈值；数组容量>=64
3.退化情况1：在扩容时如果拆分树时，树元素个数<=6则会退化链表
4.退化情况2：remove树节点时，若root、root.left、root.right、root.left.left有一个为null，也会退化为链表