Chapter 2：Grammars as a generating device

Chapter2：Grammars as a generating device

2.1 Languages as infinite sets

2.1.1 语言（Language）

计算机科学家的视角：语言包含句子（sentence），句子由单词（word / token）组成，句子拥有结构（structure）

• \(句子中的单词 + 句子结构 \rightarrow 句子的意义（meaning）\)
• 单词可再分 / 不可再分
  • 一般认为单词不可再分
  • 单词也可以看作另一种语言中的句子，这种语言的单词为字母

语言学家的视角：语言是句子的集合（set），每个句子是符号（symbol）的序列（sequence）

• 有限个数的符号的集合（set）：字母表（alphabet）
• “set”有两个含义：1）无重复；2）无序
• “sequence”表明句子中的符号是有序的

\(单词中的字母 + 单词的结构 \rightarrow 单词的意义\)，\(句子中的单词 + 句子的结构 \rightarrow 句子的意义\)

2.1.2 文法（Grammar）

句子 / 单词层次：语法（syntax）
单词 / 字母层次：文法

generative grammar：精确、固定长度（fixed-size）的规则，描述如何构造语言中的句子

也就是说，我们能够依照规则（经过有限的步骤）构造出且仅构造出语言中所有的句子（而不是构造某个特定的句子！）

2.1.3

2.1.3.3 Languages are infinite bit-strings

以字母表 \(\Sigma = \{a, b\}\) 为例，\(\Sigma^* = \{\epsilon, a, b, aa, ab, \cdots\}\)

• 任何使用字母表 \(\Sigma\) 的语言都是语言 \(\Sigma^*\) 的子集
  • 比如语言 \(L\) ：{a 的出现次数比 b 多的所有单词} \(= \{a, aa, aaa, aab, \cdots\}\)，如果用 0 表示单词（句子）不存在，1 表示单词（句子）存在，则 \(\Sigma^*\) 为全 1 的串，而 \(L = 0101000111\cdots\)

2.2 Formal Grammars

形式化定义：generative grammar 是一个四元组（4-tuple）\((V_N, V_T, R, S)\)

• \(V_N\)：所有非终结符
• \(V_T\)：所有终结符
• \(R\)：规则（Rule / Recipe）/ 产生式（Production）
  • 左边（头部）：\((V_N \cup V_T)^+\)
  • 右边（体）：\((V_N \cup V_T)^*\)
• \(S\)：开始符

2.2.1 Generating sentences from a formal grammar

中间形式：句型（sentential form），全部为非终结符的句型即为句子

2.3 文法和语言的 Chomsky 层次结构

原因：为了限制文法的不可管理性（Unmanageability），同时保证其表达能力（Generative Power）

从 0 型文法到 4 型文法，限制越来越多，表达能力越来越弱。下面一张图解释几种文法之间的关系：

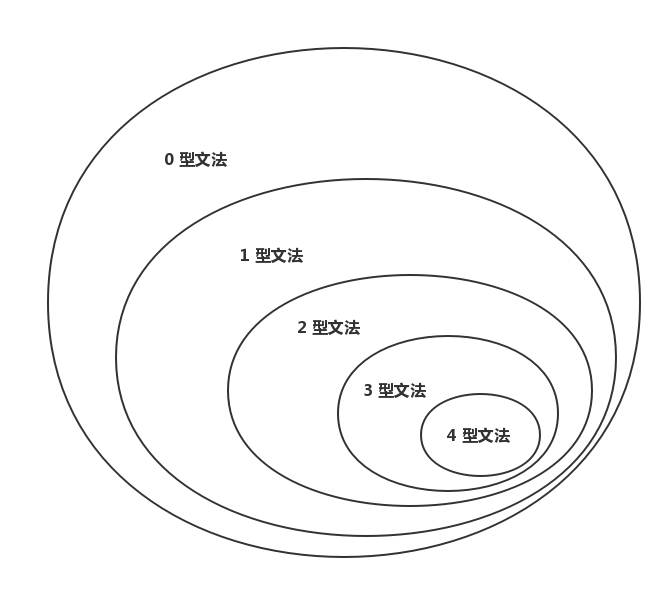
规则：

• n 型语言能够由 n 型文法产生，也可以由 0..n-1 型文法（表达能力更强）产生，但不能由表达能力更弱的文法如 n+1 型文法产生
• 某种语言能由 n 型文法产生，并不意味着一定有其相应的 n+1 型文法，但一定有其对应的 0..n-1 型文法
• 文法由其符合的最弱文法类型命名，即如果一种文法既是 0 型文法又是 1 型文法，那么通常我们称这种文法为 1 型文法

0 型文法（Type 0 Grammar，也叫 Phrase Structure Grammar（短语结构文法））

将包含任意（非零）个数符号的序列转换为包含任意个数的符号的另一序列

1 型文法（Type 1 Grammar，也叫 Context-Sensitive Grammar（上下文有关文法））

分为两种：

• Type 1 Monotonic：文法中每个产生式的左部的符号的数量不多于右部
  • 用符号语言表述：\(\alpha \rightarrow \beta\)，其中：
    • \(|\alpha| \le |\beta|\)
• Type 1 Context-Sensitive：文法中每个产生式的左部有且仅有一个非终结符被替换
  • 用符号语言表述：\(\alpha A \beta \rightarrow \alpha\omega\beta\)，其中：
    • \(\omega \in (V_T \cup V_N)^{+}\)
    • \(\alpha\) 称为上文（Left Context），\(\beta\) 称为下文（Right Context）
    • \(\alpha\) 和 \(\beta\) 均可为空，如果二者同时为空，就是上下文无关文法
  • 从上面可以看到，Type 1 Context-Sensitive 文法也是 Type 1 Monotonic 文法，因为 \(|A| \le |\omega|\)
• 二者在表达能力上是等价的

例子 1：
\(Name_1\ Comma\ Name_2\ End \rightarrow Name_1\ and\ Name_2\ End\)
其中 \(Name_1\) 是上文（Left Context），\(Name_2\) 是下文（Right Context）（下表只是为了便于区分两个非终结符）。
这个产生式表示在上文为 \(Name_1\)，下文为 \(Name_2\) 的条件下，可以应用产生式 Comma -> and，注意到产生式左部的其余部分并未改变。

例子 2（将文法改写为上下文有关文法）：

1)  Sentence -> Name | List
2)      List -> EndName | Name, List
3) , EndName -> and Name
4)      Name -> tom | dick | harry

将这个文法转换为 1 型文法的过程如下：

1. 首先，注意到产生式 3) 不符合 Context-Sensitive Grammar 的规则，所以要将其拆分
   3.1) , EndName -> and EndName
3.2) and EndName -> and Name
2. 步骤 1 中得到的文法对非终结符 and 进行了替换，不符合规则，所以引入新的非终结符 Comma，改写如下：
   3.1) Comma EndName -> and EndName
3.2) and EndName -> and Name
3.3) Comma -> ,

例子 3（由 1 型语言构造 1 型文法）：
考虑如下的语言：\(L = \{a^nb^nc^n|n \ge 0\}\)
使用逐步求精的办法：

1. 首先找特殊情况：S -> abc
2. 其次，语言中含有任意数量的 a，我们可以考虑扩展 S 的前缀，为了做到这一点，我们对 S 进行递归定义：S -> aS
3. 语言要求 a、b、c 的数量相同，为了记住有多少个 a，同时满足 b、c 在 a 后面，我们还需要加一个符号：S -> aSQ
4. 审视一下我们目前的成果，进行几次推导，得到：aaabcQQ
5. 从步骤 4 来看，如果我们想要得到 aaabbbccc，似乎应该令 Q -> bc，但是这样会导致 c 出现在 b 的前面，所以进行改写：bQc -> bbcc
6. 最后，我们需要所有的 c 在最后，可以考虑将其逐步交换至末尾，所以有产生式：cQ -> Qc
7. 得到如下的产生式：
   S -> aQS | abc
bQc -> bbcc
cQ -> Qc

我们可以验证我们的文法：（采用最左规约）

aaaabbbbcccc => aaaabbbQccc => aaaabbbcQcc => aaaabbbccQc
             => aaaabbbcccQ => ··· => aaaabcQQQ => aaaSQQQ
             => aaSQQ => ··· => S

2 型文法（Type 2 Grammar，也叫 Context-Free Grammar（上下文无关文法））

所谓 “上下文无关文法”，就是不需要上下文，所以 2 型文法实际上就是 Type 1 Context-Sensitive 文法的上下文置为空得到的文法，所以 2 型文法的所有产生式的左边都只有一个非终结符。这样一来，就不会出现 starlike form，所以 2 型文法的 production graph 就变成了一棵树，叫做 production tree。

2 型文法更侧重于展现语言的结构（Structure）。

在一种特殊情况下，2 型文法会变成非 monotinic：含有 \(\epsilon\) 产生式。没有 \(\epsilon\) 产生式的文法被称为是 \(\epsilon\)-free 的。

2 型文法的形式化表示方法

• Backus-Naur 范式（BNF）

      <name>::= tom | dick | harry
  <sentence>::= <name> | <list> and <name>
      <list>::= <name>, <list> | <name>
  

• van Wijngaarden 范式

      name: tom symbol; dick symbol; harry symbol. 
  sentence: name; list, and symbol, name. 
      list: name, comma symbol, list; name. 
  

: 读作 “被定义为”，; 读作 “，或者被定义为”，, 读作 “接着”，. 读作 “，没有其他定义”

2.3.2.3 扩展上下文无关文法（Extended Context-Free Grammar / ECF，有时也叫 Regular Right Part Grammar / RRP）

引入符号：

• *：0 次或多次
• +：1 次或多次
• ?：0 次或 1 次
• +n：1 次到 n 次
• +,：1 次或多次并由 , 分隔

对 ECF 结构的解读有两种不同的意见：

• （右）递归（多用于实践）：

  Book -> Preface a Conclusion
     a -> Chapter | a Chapter
  

• 迭代（多用于研究）：

  Book -> Preface Chapter Conclusion | Preface Chapter Chapter Conclusion | Preface Chapter Chapter Chapter Conclusion | ···
  

构造上下文无关文法

《计算理论导引》中给出了四种构造 CFG 的方法：

• 分治，某些 CFG 可以很容易的分解成互不相交的部分，我们只要分别构造这些部分的文法，最后将文法用 “|” 合并即可
• 将语言中的字符串看作两个子串的连接，这种语言要记录其中一个子串的信息以确认另一个子串的正确性，这种情况下我们可以尝试套用 \(S \rightarrow uSv\)
• 观察递归结构（直接递归 / 间接递归）
• 如果语言是正规的（3 型语言，注意 3 型语言是 2 型语言的子集），那么先构造 DFA，然后将 DFA 转化为等价的上下文无关文法
• 更多构造 CFG 的方法见另一篇博文 传送门

3 型文法（Type 3 Grammar，也叫 Regular Grammar（正规文法）或 Finite-State Grammar（有限状态文法））

3 型文法规则：

• 一个非终结符产生 0 个或 1 个终结符
• 一个非终结符产生 0 个或 1 个终结符，后面跟 1 个非终结符

Chomsky 要求必须有一个非终结符，但是上面的定义实际上与 Chomsky 的定义等价且更灵活。

符号化表述：\(A \rightarrow a | B | aB | \epsilon\)

判断语言是否是正规的（Regular）

Pumping Lemma（中文直译为 “泵引理”，很奇怪，所以下面写英文名称）：
如果 \(A\) 是正规语言，那么存在一个非零值 \(p\)（Pumping Length），对于语言 \(A\) 中任意一个长度至少为 \(p\) 的字符串 \(s\)，可以将其分为三部分，即 \(s=xyz\)，并且满足如下条件：

1. 对任意 \(i \ge 0\)，\(xy^iz \in A\)（\(y\) 可重复任意多次）
2. \(|y| \gt 0\)（\(y\) 不能为 \(\epsilon\)）
3. \(|xy| \le p\)

例子1：
证明语言 \(L = \{ 0^n 1^n | n \ge 0\}\) 是非正规（Non-Regular）的。

这个语言有两条性质：

1. 所有的 0 都出现在 1 前面
2. 0 和 1 的个数相等

使用反证法，只要能够推翻上面条件之一即可。

证明思路：
不失一般性，从语言 L 中找出一个字符串 s，将其分割成三部分 x、y、z，然后推导出矛盾（违背 Pumping Lemma 或者构造出不属于语言 L 的字符串）。

证明：

1. 令 \(n = p\)
2. 如果 \(y = 0^p\)（那么自然地，\(x=\epsilon\)，\(z=1^p\)），那么 Pumping Lemma 的条件 1 不成立（比如 \(i=0\) 时，有 \(s' = z = 1^p\)，显然 0 和 1 的个数不相等）
3. 如果 \(y = 1^p\)，结果同上
4. 如果 \(y\) 即含有0 又含有 1，比如 \(y=0^{p-1} 1^{p-1}\)（则 \(x = 0\)，\(z=1\)），那么当 \(i=2\) 时，有 \(s' = xy^2z = 00^{p-1}1^{p-1}0^{p-1}1^{p-1}1\)，违反了性质 1
   每种情况都能够导出矛盾，所以语言 L 是非正规的

例子2（利用 Pumping Lemma 的条件 3）：
证明语言 \(L = \{ 1^{n^2} | n \ge 0\}\) 是非正规的。

证明思路：
这个语言中字符串的 1 的个数都是完全平方数，即 1、4、9、16，那么我们可以由语言 L 中的某个字符串 s 构造出含有诸如 2、8、11 个 1 的字符串，导出矛盾。

证明：

1. 令 \(n=p\)，则有 \(s = 1^{p^2}\)
2. 由 Pumping Length 的条件 3 可知，子串 xy 的长度不能超过 p，所以令 \(y = 1^p\)，则 \(x = \epsilon\)，\(z = 1^{p^2-p}\)
3. 当 i = 2 时，有 \(s' = xy^2z = 1^{2p}1^{p^2-p} = 1^{p^2+p}\)，易知 \(p^2 \lt p^2+p \lt (p+1)^2 = p^2 + 2p + 1\)（因为 p > 0，所以等号不成立），即 \(s' \notin L\)，违背了 Pumping Lemma 的条件 1
   综上，语言 L 不是正规语言。

（更多的示例见《计算理论导引》1.4 非正规语言）

4 型文法（Type 4 Grammar，也叫 Finite-Choice Grammar（有限选择文法））

产生式右边不能有非终结符，只能够产生有限长度的串。

例：

S -> [tdh] | [tdh] & [tdh] | [tdh], [tdh] & [tdh]

程序设计语言中的保留字可以使用 4 型文法描述。虽然 4 型文法应用的较少，但实际上很多文法中包含有限选择的产生式。

2.4 VW 文法

文法类型的层次结构：

• Phrase Structure
• Context-Sensitive
• Context-Free
• Regular
• Finite-Choice

CS 文法和 CF 文法之间的界限比正规文法和 FC 文法之间的界限更重要。前者是全局相关性（Global Correlation）和局部独立性（Local Independence）的区别。

理论上来讲，仅仅观察邻居足够表达任意的全局关系，但是如果长范围的关系使用这种机制，会导致信息在句型中流动（Flow）很长的距离。每个产生式都要了解几乎所有其他的产生式，这使得文法会异常复杂。

2.4.2 VW 文法

CFG 只能表达有限数量的长范围关系，随着其能够表达的关系数量越来越大，文法的规则也会越来越多。如果 CFG 有无数条规则，那么它等价于 CSG。

考虑语言 \(L = \{ a^n b^n c^n | b \ge 0\}\)

第一种表示方式（无穷多条规则的 CFG）：

text:    a symbol, b symbol, c symbol;
           a symbol, a symbol,
               b symbol, b symbol,
               c symbol, c symbol;
           a symbol, a symbol, a symbol,
               b symbol, b symbol, b symbol
               c symbol, c symbol, c symbol;
           ···

第一次抽象：

text:    ai, bi, ci;
           aii, bii, cii;
           aiii, biii, ciii;
           ···

ai:       a symbol. 
aii:      a symbol, ai.
···
bi:       b symbol. 
bii:      b symbol, bi. 
···
ci:       c symbol. 
cii:      c symbol, ci.
···

第二次抽象：

text:    a N, b N, c N. 

a i:      a symbol. 
a i N:  a symbol, a N. 
b i:      b symbol. 
b i N:  b symbol, b N. 
c i:      c symbol. 
c i N:  c symbol, c N.

N::    i; i N. 

其中 N 叫做元标记（Metanotion），规则 N:: i; i N. 叫做元规则（Metarule），他们不用于产生句子，而是用于产生规则中的名字（Name）（类似于 C 语言中的宏）

第三次抽象：

text:    a N, b N, c N. 

A i:      A symbol. 
A i N:  A symbol; A N. 

N::     i; i N. 
A::     a; b; c. 

元标记的一致代换规则（Consistent Substitution Rule）：每次代换时，所有的元标记都要代入一致的符号，比如：

A i:      A symbol. 
A i N:  A symbol; A N. 

可以代换成：

a i:      a symbol. 
a i N:  a symbol, a N. 

但不能代换成：

a i:      a symbol. 
b i N:  b symbol, a N. 

如果没有一致代换规则，VW 文法等价于 CFG。

2.4.5 缀词文法（Affix Grammar）

简单来说，缀词文法由这几种元素构成：

• 变量
• 子程序
  • 类似于产生式的子程序
  • 条件判断（Primitive Predicate）（以 where is 开头）及条件成立时的动作
• 所谓的 “缀词”（Affix）就是子程序的参数

例子：

N, M:: integer. 
A, B:: a; b; c. 

text + N: list + N + a, list + N + b, list + N + c. 

list + N + A: where is zero + N; letter + A, where is decreased + M + N, list + M + A. 

letter + A: where is + A + a, a symbol;
            where is + A + b, b symbol;
            where is + A + c, c symbol.

where is zero + N: { N = 0 }. 
where is decreased + M + N: { M = N - 1 }. 
where + A + B: { A = B }.    

类似于下面的代码（经测试可运行）：

#include <stdio.h>

typedef int bool;
typedef enum {a, b, c} Symbol;

void list(int N, Symbol A);
void letter(Symbol A);
bool zero(int N);
void decreased(int *M, int *N);
bool equals(Symbol A, Symbol B);

int main(int argc, const char *argv[]) {
    list(3, a);
    list(3, b);
    list(3, c);
    putchar('\n');
    
    return 0;
}

void list(int N, Symbol A) {
    if (zero(N)) {

    } else {
        letter(A);
        int M;
        decreased(&M, &N);
        list(M, A);
    }
}

void letter(Symbol A) {
    if (A == a) {
        putchar('a');
    } else if (A == b) {
        putchar('b');
    } else {
        putchar('c');
    }
}

bool zero(int N) {
    return N == 0;
}

void decreased(int *M, int *N) {
    *M = *N - 1;
}

bool equals(Symbol A, Symbol B) {
    return A == B;
}

2.5 由文法生成句子

2.5.1 一般情况

生成所有句子的算法（实质是有向图的广度优先遍历，\(v_1 \rightarrow v_2\) 表示 \(v_1\) 可经一步推导得到 \(v_2\)）：

1. 将起始符放入队列
2. 将队首元素出队，从左向右扫描，找出所有能够进行代换的符号串（即所有出现在文法产生式左部的子串）
   2.1 如果一个符号串中没有非终结符，那么它就是一个句子，打印（或其他操作），遗弃
   2.2 如果一个符号串中含有非终结符，但是不能与任何一个产生式的左部匹配，那么就进入了死胡同（Blind Alley），遗弃
3. 将当前元素复制足够多次，并替换相应的部分，入队
4. 不断重复步骤 2、3 直到队列为空

注意：步骤 2 中，要求找出所有能够进行代换的符号串，而不仅仅是第一个匹配的。如果仅仅替换第一个，可能会产生问题：

 S -> AC
 A -> b
AC -> ac

在上面这个文法中，如果仅仅替换 S -> AC 右部的 A，得到的是 S -> bC，我们就进入了死胡同（因为破坏了上下文），而如果建立多个副本，替换所有匹配的串，即 S -> bC（剔除）和 S -> ac，我们可以得到一个句子。
另外，上下文无关文法没有这方面的限制，因为上下文无关文法所有产生式左部都只有一个非终结符，也就是说，每次最多匹配一个非终结符且不会破坏上下文。

《Parsing Techniques》还提出了两点注意事项：

• 通常情况下，我们无法预测一个文法是否真的能产生句子。存在某些算法能够确定特定的文法是否真的能产生句子，但是目前还没有一种算法对所有的文法都适用
• 我们无法预测句子产生的顺序

2.5.2 上下文无关文法的情况

确定 CFG 是否真的能产生句子的方法：
0. A = { }

1. 找出所有仅产生终结符的非终结符，加入集合 A
2. 找出所有仅产生终结符和 A 中非终结符的终结符，加入集合 A
3. 重复步骤 1、2 直至集合 A 不再产生变化
4. 如果集合 A 中不包含起始符 S，那么这个 CFG 不能产生任何句子

最左推导：每次替换最左可推导非终结符
最右推导：每次替换最右可推导非终结符
可推导：非终结符出现在某个产生式的左部
最左推导和最右推导对应相同的产生式树（Production Tree），但是遍历的顺序不同。

Parsing 的任务是重构给定输入的解析树（图）。

2.6 To Shrink Or Not to Shrink

Chomsky 层次结构只允许 0 型文法进行句型的收缩，1 到 3 型文法都必须是单调的。这样，每一类文法就是其父类的真子集，并且除了 0 型文法之外的文法的推导图实际上都是推导树。

理论上来讲，任何文法都可以转化成等价的 \(\epsilon\) - free 文法，但代价是文法变得更加晦涩。

		Chomsky 层次结构（单调的）		非单调层次结构
Global Production Effects	0 型	无限制短语结构文法	有$\epsilon$产生式的单调文法	无限制短语结构文法
	1 型	上下文相关文法	$\epsilon$ - free 的单调文法	有非单调规则的上下文有关文法
Local Production Effects	2 型	$\epsilon$ - free 的上下文无关文法		上下文无关文法
	3 型	$\epsilon$ - free 的正规文法		正规文法，正规表达式
No production	4 型	有限选择（Finite-Choice）文法

参考

[1] 《Parsing Techniques》，Dick Grune：传送门
[2] 《计算理论导引》，Michael Sipser

更多资料

[1] 《编译原理》，Aho 等
[2] 自动机理论：传送门