【论文精读】On the Relationship Between Self-Attention and Convolutional Layers

【论文精读】On the Relationship Between Self-Attention and Convolutional Layers

作者: Jean-Baptiste Cordonnier, Andreas Loukas, Martin Jaggi
发表会议: ICLR 2020
论文地址: arXiv:1911.03584v2

目录

• 【论文精读】On the Relationship Between Self-Attention and Convolutional Layers
  • 1.Introduction
    • 1.1 文章解决的问题
    • 1.2 作者给出的回答
  • 2. Background
    • 2.1 Multi-head self-attention layers
    • 2.2 Attention for images
    • 2.3 Positional encoding for images
  • 3. 理论证明
  • 4. 实验
    • 4.1 Implement details
    • 4.2 Quadratic encoding
    • 4.3 Learned relative positional encoding
  • 5. 结论

1.Introduction

1.1 文章解决的问题

"Do self-attention layers process images in a similar manner to convolutional layers? "

self-attention层是否可以执行卷积层的操作？

1.2 作者给出的回答

• 理论角度：self-attention层可以表达任何卷积层。
• 实验角度：作者构造了一个fully attentional model，模型的主要部分是六层self-attention。结果表明，对于前几层self-attention，执行了与卷积层类似的操作。

2. Background

2.1 Multi-head self-attention layers

对于第t个query token，自注意力层的输出如下：

$$\operatorname{Self-Attention}(\boldsymbol{X})_{t,:}:=\operatorname{softmax}\left(\boldsymbol{A}_{t,:}\right) \boldsymbol{X} \boldsymbol{W}_{\text {val }}\\ \text{其中},\quad\boldsymbol{A}:=\boldsymbol{X} \boldsymbol{W}_{q r y} \boldsymbol{W}_{k e y}^{\top} \boldsymbol{X}^{\top}$$

• $\boldsymbol{X} \in \mathbb{R}^{T \times D_{\text {in }}}$：输入矩阵。$T$ 个tokens，每个tokens都是 $D_{i n}$ 维的向量

• $\boldsymbol{W}_{q r y} \in \mathbb{R}^{D_{i n} \times D_k}$, $\boldsymbol{W}_{\text {key }} \in \mathbb{R}^{D_{i n} \times D_k}$ , $\boldsymbol{W}_{\text {val }} \in$ $\mathbb{R}^{D_{\text {in }} \times D_{\text {out }}}$：分别表示query，key和value的矩阵。

---

有时，我们需要给输入加上位置编码

$$\boldsymbol{A}:=(\boldsymbol{X}+\boldsymbol{P}) \boldsymbol{W}_{q r y} \boldsymbol{W}_{k e y}^{\top}(\boldsymbol{X}+\boldsymbol{P})^{\top}$$

• $\boldsymbol{P} \in \mathbb{R}^{T \times D_{\text {in }}}$：位置编码

---

有时，我们需要多头自注意力机制

$$\operatorname{MHSA}(\boldsymbol{X}):=\underset{h \in\left[N_h\right]}{\operatorname{concat}}\left[\operatorname{Self-Attention}_h(\boldsymbol{X})\right] \boldsymbol{W}_{\text {out }}+\boldsymbol{b}_{\text {out }}$$

• 在多头自注意力机制中，有$N_h$个头，每个头的输出是$D_h$维的向量，最终，$N_h$个$D_h$维的向量被映射到$D_{\text {out }}$维的输出向量上。
• $\boldsymbol{W}_{\text {out }} \in \mathbb{R}^{N_h D_h \times D_{\text {out }}}$, $\boldsymbol{b}_{\text {out }} \in \mathbb{R}^{D_{\text {out }}}$：映射矩阵和偏置
• $\underset{h \in\left[N_h\right]}{\operatorname{concat}}\left[\operatorname{Self-Attention}_h(\boldsymbol{X})\right]$：将$N_h$个头的输出拼接在一起。每个头的输出维度是 $T \times D_h$，拼接后的总输出大小会变为 $T \times\left(N_h \cdot D_h\right)$。

2.2 Attention for images

一个“像素”的含义：例如在下图中，一个vector就是一个像素

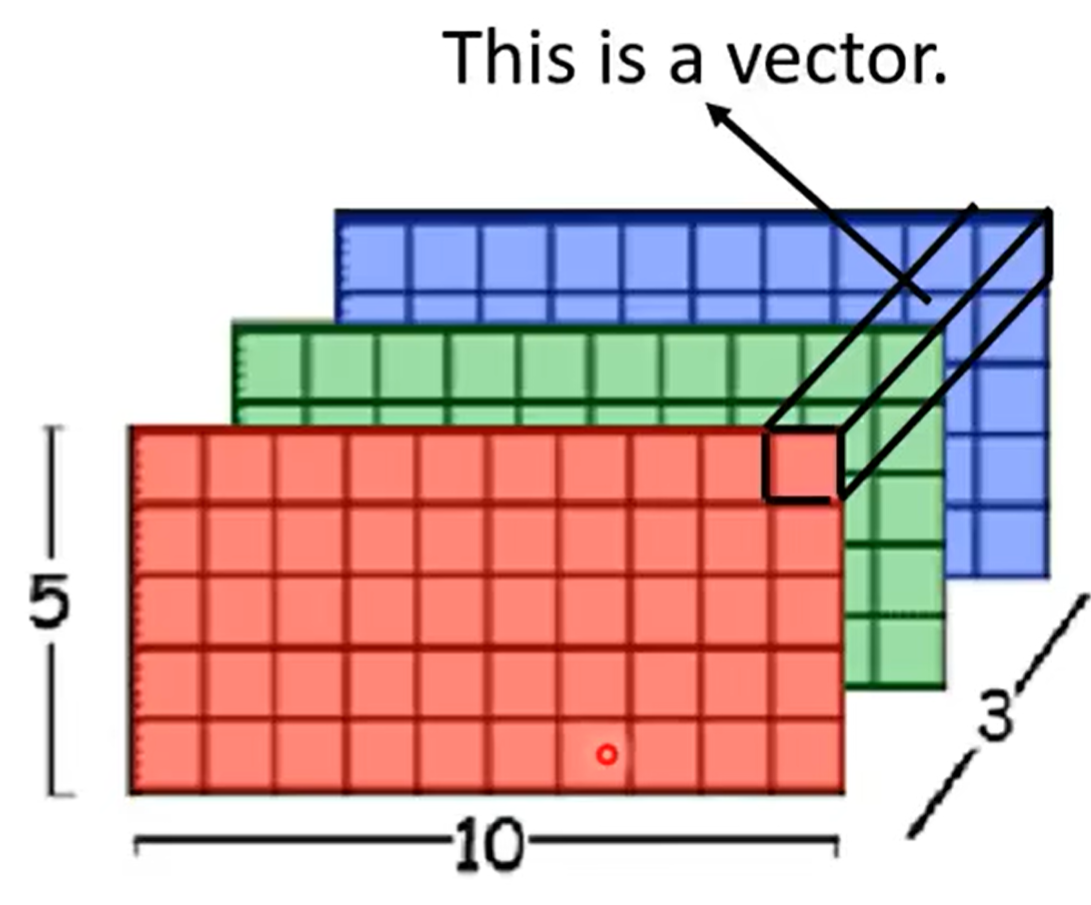
给定图像向量 $\mathbf{X} \in \mathbb{R}^{W \times H \times D_{i n}}$ ，其中宽度为 $W$，高度为 $H$ ，通道数为 $D_{i n}$ 。对于其中的像素 $(i, j)$，卷积层的输出为

$$\operatorname{Conv}(\boldsymbol{X})_{i, j,:}:=\sum_{\left(\delta_1, \delta_2\right) \in \mathbb{\Delta}_K} \mathbf{X}_{i+\delta_1, j+\delta_2,:} \mathbf{W}_{\delta_1, \delta_2,:,:}+\boldsymbol{b}$$

其中 $\mathbf{W}$ 是 $K \times K \times D_{\text {in }} \times D_{\text {out }}$大小的权重，$\boldsymbol{b} \in \mathbb{R}^{D_{\text {out }}}$ 是偏置，

集合$\Delta_K$定义如下

$$\Delta_K:=\left[-\left\lfloor\frac{K}{2}\right\rfloor, \cdots,\left\lfloor\frac{K}{2}\right\rfloor\right] \times\left[-\left\lfloor\frac{K}{2}\right\rfloor, \cdots,\left\lfloor\frac{K}{2}\right\rfloor\right]$$

包含了 $K \times K$ 卷积核中所有可能出现的偏移。

---

将一个像素看成一个token，就可以实现对图像的self-attention操作。

若 $\boldsymbol{p}=(i, j)$, 那么将$\mathbf{X}_{i, j,:}$ ，$\mathbf{A}_{i, j,:,:}$ 分别记作 $\mathbf{X}_{\boldsymbol{p},:}$ ， $\mathbf{A}_{\boldsymbol{p},:}$

$$\operatorname{Self-Attention}(\boldsymbol{X})_{\boldsymbol{q},:}=\sum_{\boldsymbol{k}} \operatorname{softmax}\left(\mathbf{A}_{\boldsymbol{q},:}\right)_{\boldsymbol{k}} \mathbf{X}_{\boldsymbol{k},:} \boldsymbol{W}_{\text {val }}$$

• $\boldsymbol{q}$：query的像素
• $\boldsymbol{k}$：key的像素

2.3 Positional encoding for images

有两种位置编码，分别是绝对位置编码和相对位置编码。

• 绝对位置编码：每个像素 $\boldsymbol{p}$都对应着一个位置编码 $\mathbf{P}_{\boldsymbol{p}, \text { : }}$ ，绝对位置编码的注意力分数如下：
  $$\begin{aligned} \mathbf{A}_{q, \boldsymbol{k}}^{\mathrm{abs}}&=\left(\mathbf{X}_{q,:}+\mathbf{P}_{q,:}\right) \boldsymbol{W}_{q r y} \boldsymbol{W}_{k e y}^{\top}\left(\mathbf{X}_{k,:}+\mathbf{P}_{k,:}\right)^{\top} \\ & =\mathbf{X}_{q,:} \boldsymbol{W}_{q r y} \boldsymbol{W}_{k e y}^{\top} \mathbf{x}_{k,:}^{\top}+\mathbf{X}_{q,:} \boldsymbol{W}_{q r y} \boldsymbol{W}_{k e y}^{\top} \mathbf{P}_{k,:}^{\top}+\mathbf{P}_{q,:} \boldsymbol{W}_{q r y} \boldsymbol{W}_{k e y}^{\top} \mathbf{X}_{k,:}+\mathbf{P}_{q,:} \boldsymbol{W}_{q r y} \boldsymbol{W}_{k e y}^{\top} \mathbf{P}_{\boldsymbol{k},:} \end{aligned}$$

---

• 相对位置编码：只算query像素和key像素之间的位置差$\boldsymbol{\delta}:=\boldsymbol{k}-\boldsymbol{q}$，每个$\boldsymbol{\delta}$都有对应一个位置编码$\boldsymbol{r}_{\boldsymbol{\delta}}$。相对位置编码的注意力分数如下：

  $$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}^{\mathrm{rel}}:=\mathbf{X}_{\boldsymbol{q},:}^{\top} \boldsymbol{W}_{q r y}^{\top} \boldsymbol{W}_{k e y} \mathbf{X}_{k,:}+\mathbf{X}_{\boldsymbol{q},:}^{\top} \boldsymbol{W}_{q r y}^{\top} \widehat{\boldsymbol{W}}_{k e y} \boldsymbol{r}_{\boldsymbol{\delta}}+\boldsymbol{u}^{\top} \boldsymbol{W}_{k e y} \mathbf{X}_{k,:}+\boldsymbol{v}^{\top} \widehat{\boldsymbol{W}}_{k e y} \boldsymbol{r}_{\boldsymbol{\delta}}$$
  • $\boldsymbol{u}$ ， $\boldsymbol{v}$ ：是需要学习的两个向量，每个头都对应着一组 $\boldsymbol{u}$ ， $\boldsymbol{v}$
  • $\boldsymbol{r}_{\boldsymbol{\delta}} \in \mathbb{R}^{D_p}$：${D_p}$维的相对位置编码，所有的头共享一个$\boldsymbol{r}_{\boldsymbol{\delta}}$
  • $\boldsymbol{W}_{k e y}$，$\widehat{\boldsymbol{W}}_{k e y}$：$\boldsymbol{W}_{k e y}$是输入的权重，$\widehat{\boldsymbol{W}}_{k e y}$是相对位置编码的权重

3. 理论证明

结论：

$N_h$ 个头、每个头的输出是 $D_h$维、 最终的输出是 $D_{\text {out }}$ 维、相对位置编码维度$D_p \geq 3$的多头自注意力层，可以表示任意 卷积核大小是$\sqrt{N_h} \times \sqrt{N_h}$、输出通道数是$\min \left(D_h, D_{\text {out }}\right)$的卷积层。

• 引理1概述：对于大小为 $K \times K$ 的卷积核，其偏移位置可以表示为$\Delta_K=$ $\{-\lfloor K / 2\rfloor, \ldots,\lfloor K / 2\rfloor\}^2$ 。如果我们让每个头只关注卷积核中的一个偏移位置，那么$K^2$个头就可以模拟整个卷积核。

---

• 引理2概述：存在这样的相对位置编码，使得每个头只关注卷积核中的一个偏移位置。

  论文中，相对位置编码可以自己构造，也可以用模型来学习。

  自己构造的相对位置编码叫做quadratic encoding,其中

  $$\boldsymbol{v}^{(h)}:=-\alpha^{(h)}\left(1,-2 \boldsymbol{\Delta}_1^{(h)},-2 \boldsymbol{\Delta}_2^{(h)}\right) \quad \boldsymbol{r}_{\boldsymbol{\delta}}:=\left(\|\boldsymbol{\delta}\|^2, \boldsymbol{\delta}_1, \boldsymbol{\delta}_2\right) \quad \boldsymbol{W}_{q r y}=\boldsymbol{W}_{\text {key }}:=\mathbf{0} \quad \widehat{\boldsymbol{W}_{k e y}}:=\boldsymbol{I}$$

  参数 $\boldsymbol{\Delta}^{(h)}=\left(\boldsymbol{\Delta}_1^{(h)}, \boldsymbol{\Delta}_2^{(h)}\right)$ 表示每个头应该关注哪个偏移位置，参数 $\alpha^{(h)}$ 表示除了应该关注的偏移位置之外，是否还要关注其他偏移位置，$\boldsymbol{\Delta}^{(h)},\alpha^{(h)}$都是可学习的参数。同时, $\boldsymbol{\delta}=\left(\boldsymbol{\delta}_1, \boldsymbol{\delta}_2\right)$ 表示query像素和key像素的相对偏移，是固定的。

建议看完引理1和引理2的证明之后再来回看引理1概述和引理2概述，会有不一样的理解

---

• padding：self-attention 层默认使用SAME填充，即输入维度和输出维度相等。对于卷积，只需要令$padding = \lfloor K / 2\rfloor$，其中卷积核大小为$K\times K$，即可同样实现SAME填充。

• stride：在self-attention层后面加上一个池化层，就可以模拟任何stride的卷积。

• 空洞卷积：人为的设置self-attention中每个注意力头的关注中心$\boldsymbol{\Delta}^{(h)}$，就可以模拟任何空洞卷积。

---

引理1：

考虑这样一个多头注意力层：有$N_h=K^2$ 个头，且 $D_h \geq D_{\text {out }}$。令 $\boldsymbol{f}:\left[N_h\right] \rightarrow \Delta_K$ 是一个双射。假设对于每个头来说，都有

$$\operatorname{softmax}\left(\boldsymbol{A}_{\boldsymbol{q},:}^{(h)}\right)_{\boldsymbol{k}}= \begin{cases}1 & \text { if } \boldsymbol{f}(h)=\boldsymbol{q}-\boldsymbol{k} \\ 0 & \text { otherwise. }\end{cases}$$

那么,对卷积核大小为 $K \times K$ ，输出通道数为 $D_{\text {out }}$ 的任意卷积层，存在$\left\{\boldsymbol{W}_{\text {val }}^{(h)}\right\}_{h \in\left[N_h\right]}$ ，使得 $\operatorname{MHSA}(\boldsymbol{X})=\operatorname{Conv}(\boldsymbol{X})$对任意 $\boldsymbol{X} \in \mathbb{R}^{W \times H \times D_{i n}}$成立。

• 如何理解 $\operatorname{softmax}\left(\boldsymbol{A}_{\boldsymbol{q},:}^{(h)}\right)_{\boldsymbol{k}}= \begin{cases}1 & \text { if } \boldsymbol{f}(h)=\boldsymbol{q}-\boldsymbol{k} \\ 0 & \text { otherwise. }\end{cases}$：

  前面我们说过，要让每个头只关注卷积核中的一个偏移位置。因此，我们可以构建一个映射$\boldsymbol{f}$，规定哪个头关注哪个偏移位置。例如，$f(1)$表示第1个头应该关注哪个偏移位置，$f(2)$表示第2个头应该关注哪个偏移位置。

  对于第1个头来说，当query像素$\boldsymbol{q}$和key像素$\boldsymbol{k}$的相对偏移为$f(1)$时，$\boldsymbol{q}$和$\boldsymbol{k}$的相关性概率为1；当$\boldsymbol{q}$和$\boldsymbol{k}$的相对偏移不是$f(1)$时，相关性概率为0。

  将上面的过程用公式表示出来，就是

  $$\operatorname{softmax}\left(\boldsymbol{A}_{\boldsymbol{q},:}^{(h)}\right)_{\boldsymbol{k}}= \begin{cases}1 & \text { if } \boldsymbol{f}(h)=\boldsymbol{q}-\boldsymbol{k} \\ 0 & \text { otherwise. }\end{cases}$$

---

• 引理1的证明：

  我们将多头自注意力的公式表示为以下形式：

  $$\operatorname{MHSA}(\boldsymbol{X})=\boldsymbol{b}_{\text {out }}+\sum_{h \in\left[N_h\right]} \operatorname{softmax}\left(\boldsymbol{A}^{(h)}\right) \boldsymbol{X} \underbrace{\boldsymbol{W}_{\text {val }}^{(h)} \boldsymbol{W}_{\text {out }}\left[(h-1) D_h+1: h D_h+1\right]}_{\boldsymbol{W}^{(h)}}$$

  可以将$\boldsymbol{W}_{\text {val }}^{(h)} \boldsymbol{W}_{\text {out }}\left[(h-1) D_h+1: h D_h+1\right]$合并为$\boldsymbol{W}^{(h)}$.

  对于像素$\boldsymbol {q}$来说，公式变为

  $$\operatorname{MHSA}(\boldsymbol{X})_{\boldsymbol{q},:}=\sum_{h \in\left[N_h\right]}\left(\sum_{\boldsymbol{k}} \operatorname{softmax}\left(\mathbf{A}_{\boldsymbol{q},:}^{(h)}\right)_{\boldsymbol{k}} \mathbf{X}_{\boldsymbol{k},:}\right) \boldsymbol{W}^{(h)}+\boldsymbol{b}_{\text {out }}$$

  由于引理1中的条件, 对于第$h$个头 ，当且仅当$\boldsymbol{k}$和$\boldsymbol{q}$的相对偏移为$f(h)$时，相关性概率为 1，因此有

$$\operatorname{MHSA}(\mathbf{X})_{\boldsymbol{q}}=\sum_{h \in\left[N_h\right]} \mathbf{X}_{\boldsymbol{q}-\boldsymbol{f}(h),:} \boldsymbol{W}^{(h)}+\boldsymbol{b}_{\text {out }}$$

卷积层的公式为

$$\operatorname{Conv}(\boldsymbol{X})_{i, j,:}:=\sum_{\left(\delta_1, \delta_2\right) \in \mathbb{\Delta}_K} \mathbf{X}_{i+\delta_1, j+\delta_2,:} \mathbf{W}_{\delta_1, \delta_2,:,:}+\boldsymbol{b}$$

此时若$K=\sqrt{N_h}$，$\boldsymbol{q} = (i,j)$，$\boldsymbol{b}_{\text {out }} = \boldsymbol{b}$，

则有

$$\operatorname{MHSA}(\mathbf{X})_{\boldsymbol{q}} =\operatorname{Conv}(\boldsymbol{X})_{\boldsymbol{q}}$$

其中$\boldsymbol{W}^{(h)}$和$\mathbf{W}_{\delta_1, \delta_2,:,:}$一一对应。

---

• $D_h$ 和 $D_{\text {out }}$：对于被self-attention表示的卷积，其输出通道是$\min \left(D_h, D_{\text {out }}\right)$。因此，我们可以令$D_h = D_{\text {out }}$，来防止$D_h$或者$D_{out}$的浪费。

---

引理2：存在一种相对编码方案 $\left\{\boldsymbol{r}_{\boldsymbol{\delta}} \in \mathbb{R}^{D_p}\right\}_{\boldsymbol{\delta} \in \mathbb{Z}^2}$ ，其中维度 $D_p \geq 3$ ，以及一组参数$\boldsymbol{W}_{\text {qry }}, \boldsymbol{W}_{\text {key }}, \widehat{\boldsymbol{W}}_{\text {key }}, \boldsymbol{u}$ ，其中 $D_p \leq D_k$ ，使得对于任意 $\boldsymbol{\Delta} \in \boldsymbol{\Delta}_K$ ，都存在向量 $\boldsymbol{v}$ ( $\boldsymbol{v}$ 取决于$\boldsymbol{\Delta})$ 可以满足条件 $\operatorname{softmax}\left(\boldsymbol{A}_{\boldsymbol{q},:}^{(h)}\right)_{\boldsymbol{k}}= \begin{cases}1 & \text { if } \boldsymbol{q}-\boldsymbol{k} = \boldsymbol{\Delta} \\ 0 & \text { otherwise. }\end{cases}$

• 引理2的证明：构造了一种维度$D_p=3$的相对位置编码

  我们令$\boldsymbol{W}_{k e y}=\boldsymbol{W}_{q r y}=\mathbf{0}$ ，$\widehat{\boldsymbol{W}}_{\text {key }} \in \mathbb{R}^{D_k \times D_p}$ 为单位矩阵。根据相对位置编码公式，有 $\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}=\boldsymbol{v}^{\top} \boldsymbol{r}_{\boldsymbol{\delta}}$ ，其中 $\boldsymbol{\delta}:=\boldsymbol{k}-\boldsymbol{q}$。

  假设可以把$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}$写成如下形式：

  $$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}=-\alpha\left(\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2+c\right)$$

  其中 $c$为常数.

  在上面的式子中，$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}$的值主要取决于$-\alpha c$，当 $\boldsymbol{\delta}=\boldsymbol{\Delta}$时，$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}} = -\alpha c$。

  因此，$-\alpha c$可以理解为缩放$\mathbf{A}_{q, \Delta}$和其他注意力分数之间差距参数。

  （$\mathbf{A}_{q, \Delta}$和其他注意力分数的差距为$-\alpha\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2$，当$-\alpha c$很大时，$-\alpha\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2$占的比例很小，因此可以说，$\mathbf{A}_{q, \Delta}$和其他注意力分数的差距不大。 反之，$-\alpha c$很小时，$-\alpha\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2$占的比例很大，$\mathbf{A}_{q, \Delta}$和其他注意力分数的差距很大。）

  当 $\boldsymbol{\delta}=\boldsymbol{\Delta}$时， 有

  $$\begin{aligned} \lim _{\alpha \rightarrow \infty} \operatorname{softmax}\left(\mathbf{A}_{\boldsymbol{q},:}\right)_{\boldsymbol{k}} & =\lim _{\alpha \rightarrow \infty} \frac{e^{-\alpha\left(\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2+c\right)}}{\sum_{\boldsymbol{k}^{\prime}} e^{-\alpha\left(\left\|\left(\boldsymbol{k}-\boldsymbol{q}^{\prime}\right)-\boldsymbol{\Delta}\right\|^2+c\right)}} \\ & =\lim _{\alpha \rightarrow \infty} \frac{e^{-\alpha\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2}}{\sum_{\boldsymbol{k}^{\prime}} e^{-\alpha\left\|\left(\boldsymbol{k}-\boldsymbol{q}^{\prime}\right)-\boldsymbol{\Delta}\right\|^2}}=\frac{1}{1+\lim _{\alpha \rightarrow \infty} \sum_{\boldsymbol{k}^{\prime} \neq \boldsymbol{k}} e^{-\alpha\left\|\left(\boldsymbol{k}-\boldsymbol{q}^{\prime}\right)-\boldsymbol{\Delta}\right\|^2}}=1 \end{aligned}$$

  对于 $\boldsymbol{\delta} \neq \boldsymbol{\Delta}$，有 $\lim _{\alpha \rightarrow \infty} \operatorname{softmax}\left(\mathbf{A}_{\boldsymbol{q},:}\right)_{\boldsymbol{k}}=0$。

  因此，当$\alpha \to \infty$时，恰好满足引理2中的条件。

  那么是否存在$\boldsymbol{v},\ \boldsymbol{r}_{\boldsymbol{\delta}}$，使得$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}=\boldsymbol{v}^{\top} \boldsymbol{r}_{\boldsymbol{\delta}} = -\alpha\left(\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2+c\right)$呢？

  我们有$-\alpha\left(\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2+c\right)=-\alpha\left(\|\boldsymbol{\delta}\|^2+\|\boldsymbol{\Delta}\|^2-2\langle\boldsymbol{\delta}, \boldsymbol{\Delta}\rangle+c\right)$。

  现在我们令$\boldsymbol{v}=-\alpha\left(1,-2 \boldsymbol{\Delta}_1,-2 \boldsymbol{\Delta}_2\right)$ ，以及 $\boldsymbol{r}_{\boldsymbol{\delta}}=\left(\|\boldsymbol{\delta}\|^2, \boldsymbol{\delta}_1, \boldsymbol{\delta}_2\right)$, 那么

  $$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}=\boldsymbol{v}^{\top} \boldsymbol{r}_{\boldsymbol{\delta}}=-\alpha\left(\|\boldsymbol{\delta}\|^2-2 \boldsymbol{\Delta}_1 \boldsymbol{\delta}_1-2 \boldsymbol{\Delta}_2 \boldsymbol{\delta}_2\right)=-\alpha\left(\|\boldsymbol{\delta}\|^2-2\langle\boldsymbol{\delta}, \boldsymbol{\Delta}\rangle\right)=-\alpha\left(\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2-\|\boldsymbol{\Delta}\|^2\right)$$

  其中 常数$c=-\|\boldsymbol{\Delta}\|^2$ 。

  至此，我们成功找到了$\boldsymbol{v},\ \boldsymbol{r}_{\boldsymbol{\delta}}$，使得$\mathbf{A}_{\boldsymbol{q}, \boldsymbol{k}}=\boldsymbol{v}^{\top} \boldsymbol{r}_{\boldsymbol{\delta}} = \alpha\left(\|\boldsymbol{\delta}-\boldsymbol{\Delta}\|^2+c\right)$。

• $\alpha$：理论上，$\alpha$应该是无穷大。但在实际中，其他像素的注意力概率会随着$\alpha$的增长以指数形式趋近于 0，因此，如果32位浮点数的下界是$10^{-45}$，那么只需要令$\alpha = 46$就能满足要求。

• 根据上面所说，当$\boldsymbol{\Delta}^{(h)}$一一对应于$\Delta_K$中的元素,且$\alpha^{(h)}\ge 46$时，注意力层可以完美模拟卷积层。那么，为什么将$\boldsymbol{\Delta}^{(h)}=\left(\boldsymbol{\Delta}_1^{(h)}, \boldsymbol{\Delta}_2^{(h)}\right)$和$\alpha^{(h)}$设置成可学习的？

  让模型自主学习，可以取得更好得泛化效果。在实验中可以看到，在自主学习$\boldsymbol{\Delta}^{(h)}$和$\alpha^{(h)}$后，模型既可以执行卷积操作；又可以执行卷积所不能执行的操作，是对卷积层的一般化。

4. 实验

4.1 Implement details

fully attentional model模型：

• fully attentional model包含 6 层多头自注意力层，每层有 9 个注意力头，模拟 3×3 卷积核的局部性。
• 每层使用二次位置编码或学习位置编码，以捕捉空间信息。
• 此外，模型在输入图像上进行 2×2 下采样，以减少计算量。
• 最后一层通过平均池化汇总特征，并送入线性分类器进行预测。
• 在部分实验中还加入了内容自适应注意力，使注意力得分根据像素内容进行自适应调整。

下面是fully attentional model和CIFAR-10上与ResNet18的比较

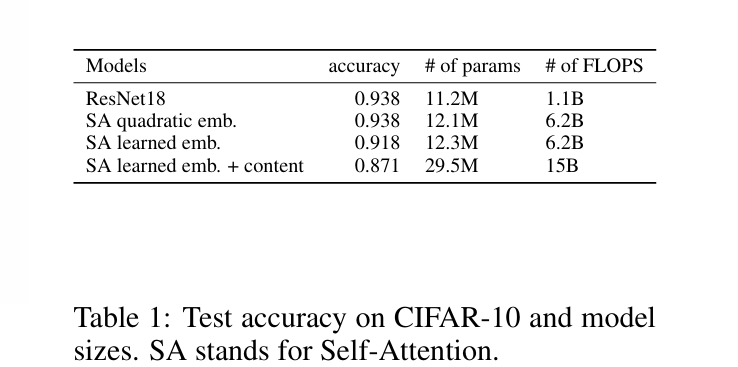
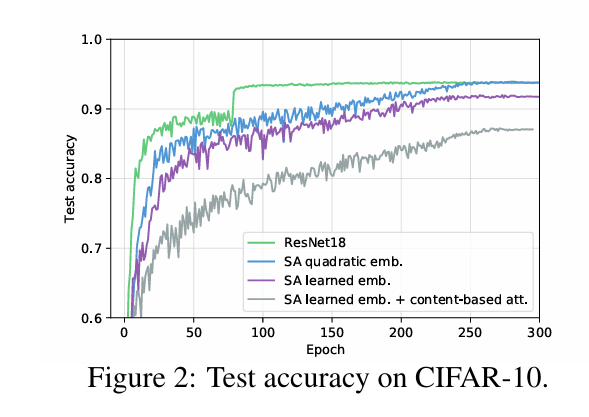
fully attentional model比ResNet18慢，不知道是代码优化的问题还是架构的问题。作者相信通过优化，二者的性能差距可以被抹平。

4.2 Quadratic encoding

每个多头自注意力层有 9 个注意力头，每个头关注的中心位置初始化为$\boldsymbol{\Delta}^{(h)} \sim \mathcal{N}\left(\mathbf{0}, 2 \boldsymbol{I}_2\right)$

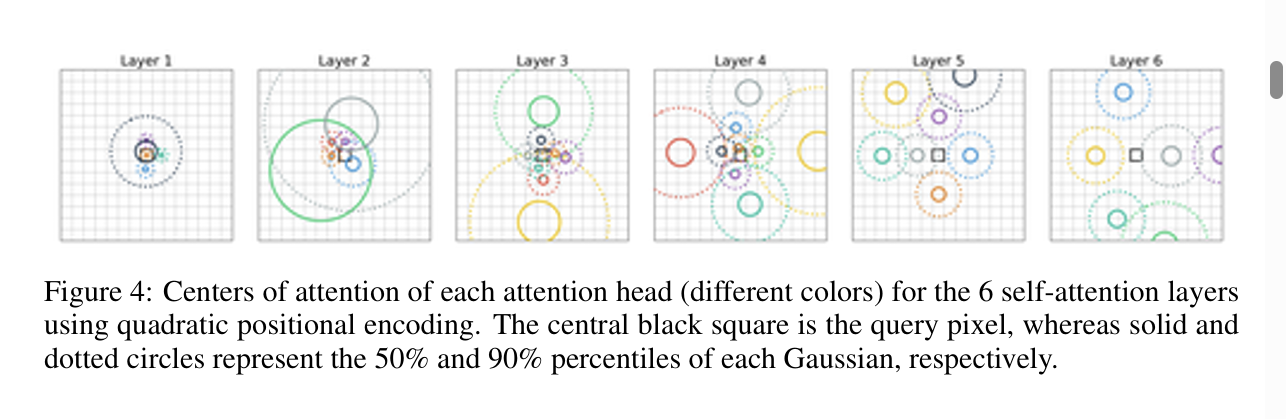
下图是第4层多头自注意力层中，每个头的$\boldsymbol{\Delta}^{(h)}$结果（每种颜色代表一个头的 $$\boldsymbol{\Delta}^{(h)}$$ ）。可以看到，9个头合在一起确实可以模拟卷积层。

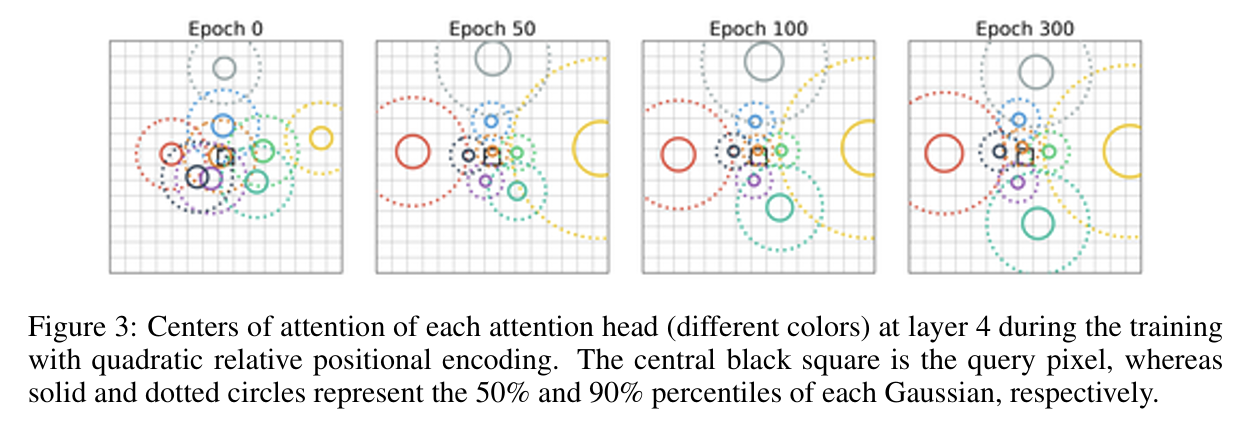
图4是训练结束之后，各个层中，每个头的$\boldsymbol{\Delta}^{(h)}$。前几层中，注意力头倾向于关注局部模式，而更深的层则倾向于关注更大的模式。

4.3 Learned relative positional encoding

让模型自主学习相对位置编码时，query像素的相关性得分如下（红色越深代表得分越高）

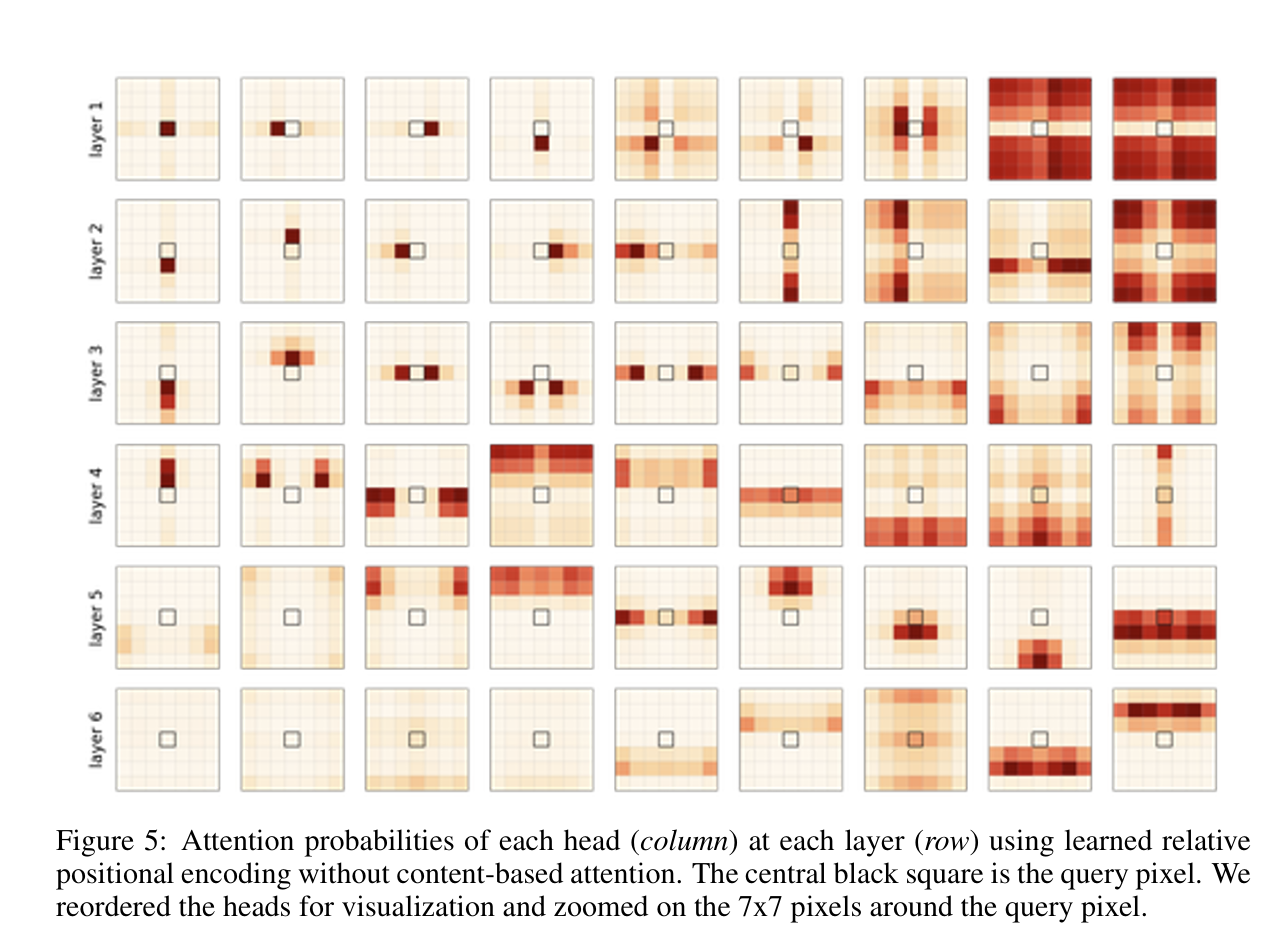
可以发现

• 有类似卷积的操作：第1，第2和第3层中的某些头关注单个像素，与引理 1 非常吻合。
• 也可以执行卷积不能执行的操作：其他头会关注水平对称的模式，以及长距离像素间的相关性。

此外，作者还加入了基于内容的注意力机制(content-based attention)。当content-based attention与模型自主学习的相对位置编码结合后，相关性得分如下：

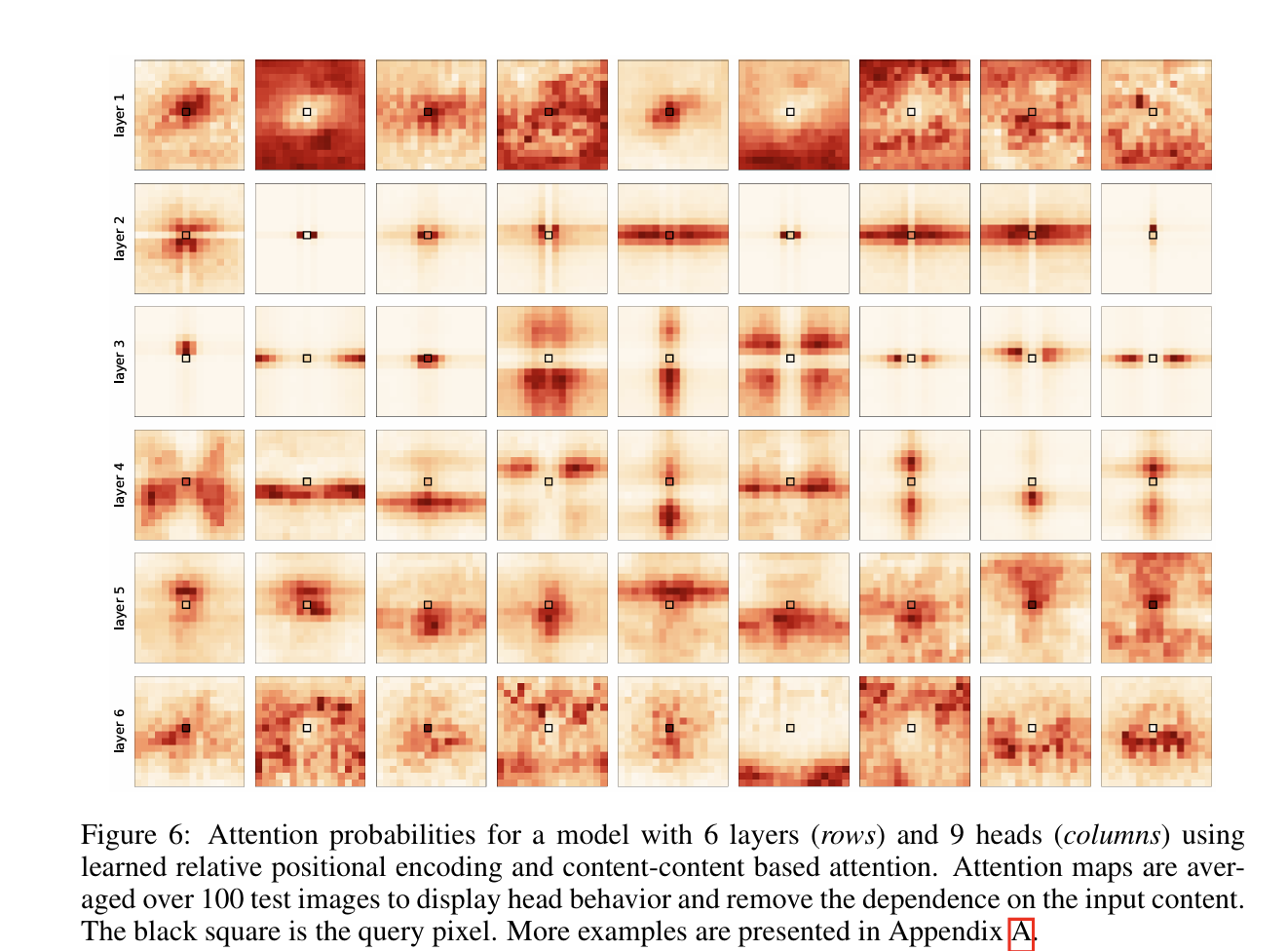
可以发现：

• 有类似卷积的操作：即使加入了content-based attention，2，3层中的某些头也只是利用相对位置来计算相关性，就像卷积核的感受野一样，利用相对位置计算。
• 也可以执行卷积不能执行的操作：其他头使用了更多的基于内容的注意力。

5. 结论

• 理论上：头部数量足够时，self-attention可以表示任意的卷积层。
• 实验： fully attentonal model既可以学习像卷积层一样学习局部模式，也可以学习全局模式。因此fully attentonal model是一般化的CNN。
• 未来工作方向：将CNN中的观点应用到transformer上。