【神经网络组件】attention层
attention层最早由Google提出,用在了Transformer中。如今,attention已经成为一种范式,可以用在深度学习的各种之中。
attention有什么用:如果当前输入为\(x\),并且你能感觉到,有一系列数据\(\{x_1,x_2,\cdots,x_n\}\)都和\(x\)有关,那么,如果单独把\(x\)作为模型的输入,会丢失部分信息。为此,你需要把\(\{x_1,x_2,\cdots,x_n\}\)也考虑进去。怎么办?
方法1:把\(\{x_1,x_2,\cdots,x_n\}\)和\(x\)一起作为模型的输入,丢给模型
问题:\(\{x_1,x_2,\cdots,x_n\}\)可能会非常非常长,一起输入到模型中,可能会导致模型过于复杂
方法2:计算\(x_1,x_2,\cdots,x_n,x\)的均值,作为模型的输入
问题:在\(\{x_1,x_2,\cdots,x_n\}\)中,有的对\(x\)的影响很大,有的对\(x\)的影响很小,应该给\(x_1,x_2,\cdots,x_n\)不同的权重。
方法3:能不能让模型自己计算\(x_1,x_2,\cdots,x_n\)的权重?
这个任务可以交给attention来完成!
1. 引入self-attention
之前,我们讲的都是输入为一个向量的情况。如果输入是一个由向量组成的sequence,并且sequence长度不定,这时我们应该用什么模型来训练?
在哪些时候,输入是一个由向量组成的sequence,并且sequence长度不定?
-
输入是一个句子:句子中的一个单词就是一个向量。可以使用one-hot编码或者Embedding技术将单词转换为向量。
-
输入是一段声音:一段声音中的每25ms就是一个向量,向量之间的间隔是10ms。例如, 0-25ms为一个向量,10-25ms为一个向量,20-35ms为一个向量,1s的声音中有100个向量。
-
输入是一个图:例如社交网络,图每一个节点可以看作一个向量(里面包含了年龄,性别,职业等信息)
-
一个分子可以看作一个向量组:其中一个原子就是一个向量
当模型的输入是一个由向量组成的sequence时,模型的输出是什么?
-
sequence中的每一个向量都对应着一个label(例如:词性标注)
-
整个sequence只输出一个label(例如:句子情感判断)
-
不知道需要输出多少个label,机器自己决定(例如,机器翻译)
为了方便,下面只讨论第一种类型的输出,即每个向量都有一个label的情况:
直觉的想法:训练一个全连接网络,对于每个向量,输出对应的label
问题:词性标注:I saw a saw(两个saw是一样的,所以网络输出一样,实际上,第一个saw是v,第二个saw是n)
有些时候,我们需要考虑上下文来输出label。那么如何考虑上下文?
一个想法是把输入向量的前后的几个向量一起输入。
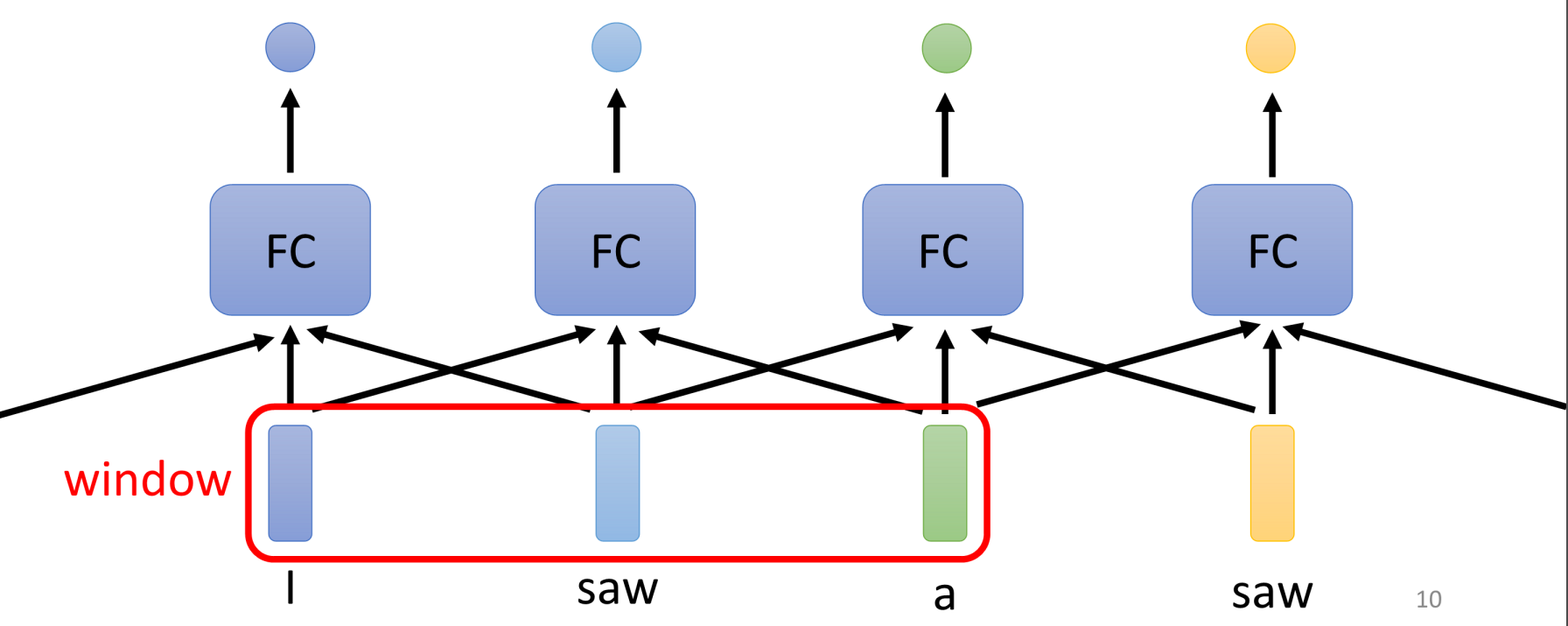
但是,如果想要整个sequence都考虑进来怎么办?
窗口增大?但是sequence有长有短,长的sequence可能非常长,如果都作为全连接网络的输入,那么网络太复杂了。
怎么办?
2. self-attention
可以在全连接层之前加一个self-attention层。
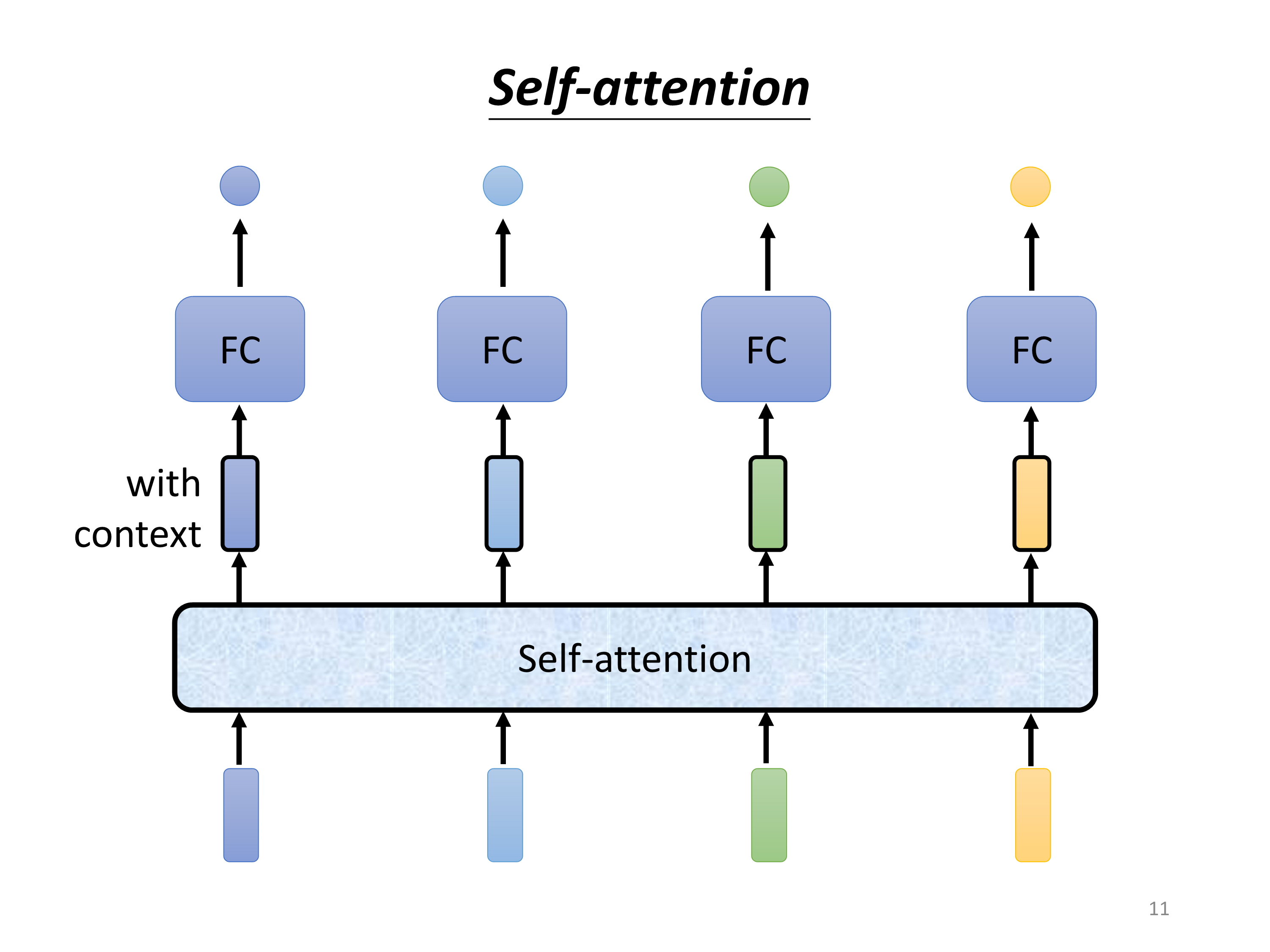
self-attetion可以多层使用,或者可以和全连接层交替使用。
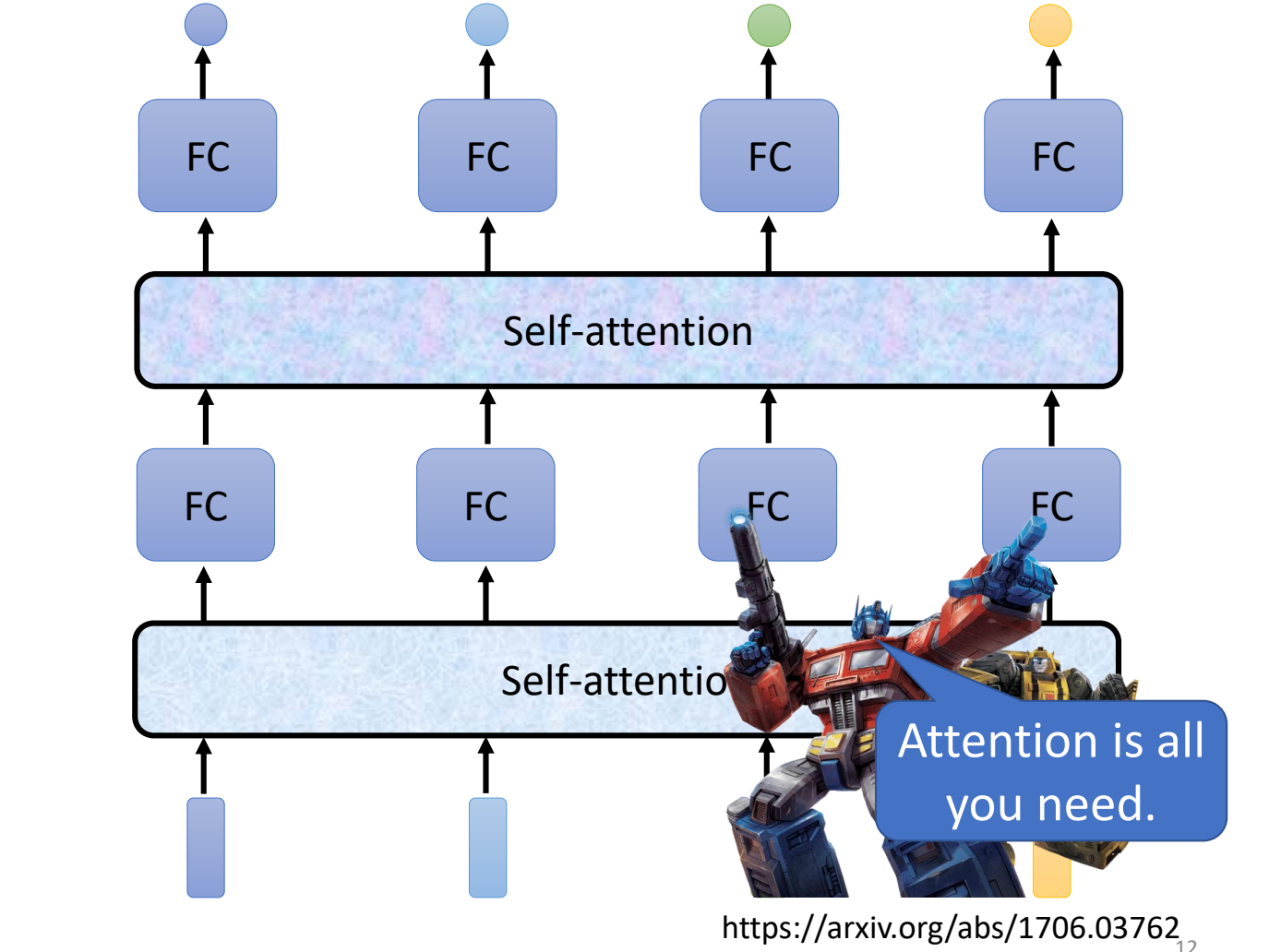
其中self-attetion处理整个sequence的信息,FC关注于处理sequence中单个向量的信息。
self-attention层是怎么工作的呢?
-
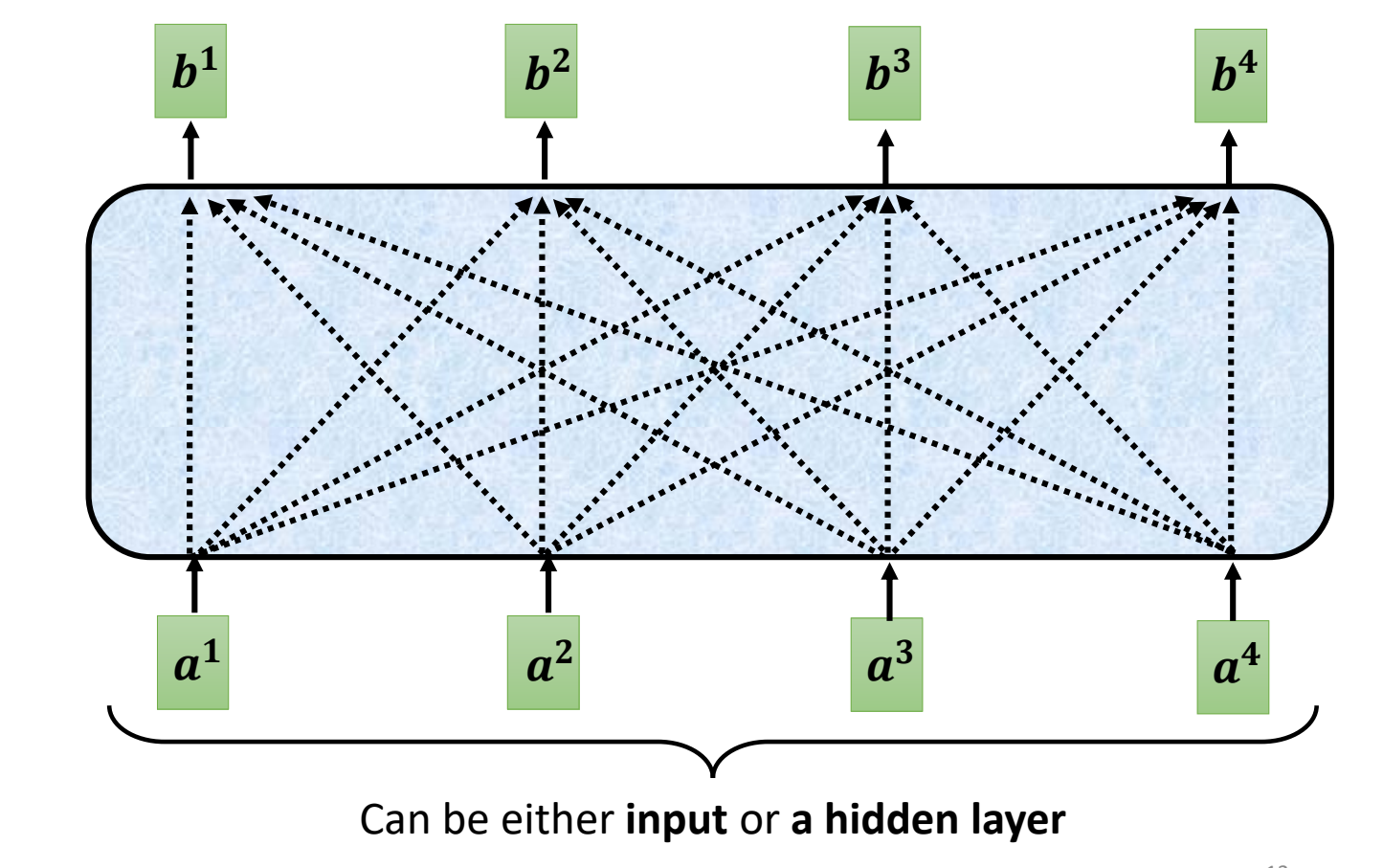
输入:模型的初始输入或者是某一个隐藏层的输出
-
输出:\(b^{(i)}\)。每个输入\(a^{(i)}\)都对应一个输出\(b^{(i)}\)。每一个\(b^{(i)}\)都是考虑了所有的输入才产生的
-
如何产生\(b^{(i)}\)呢(以\(b^{(1)}\)为例)?
-
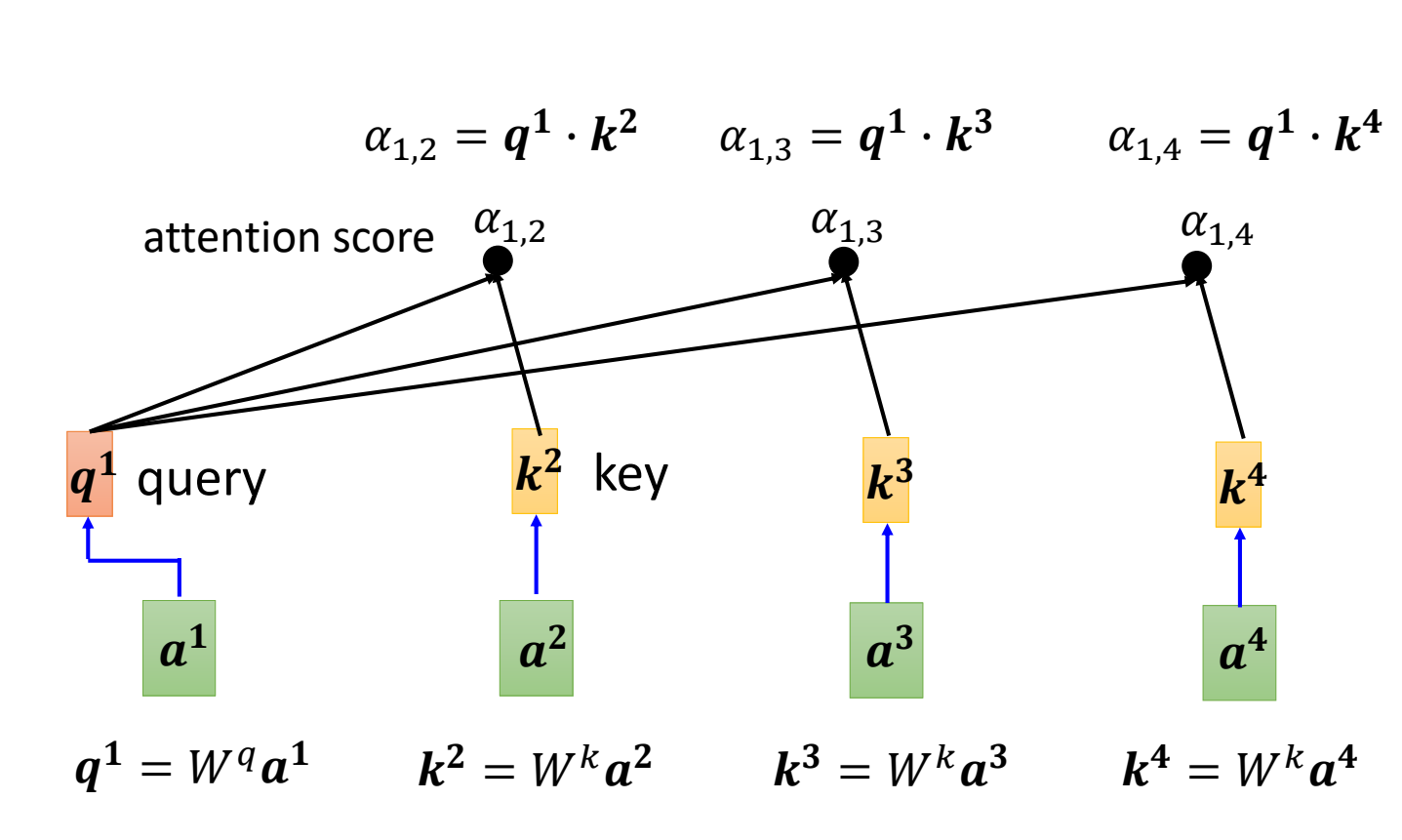
根据\(a^{(1)}\)找到sequence中所有和\(a^{(1)}\)中相关的向量(即除了\(a^{(1)}\)本身之外,还有哪些输入可以决定输出\(b^{(1)}\))。\(a^{(i)}\)和\(a^{(1)}\)相关性取值使用\(\alpha\)来表示
如何计算\(\alpha_{1,i}\)?
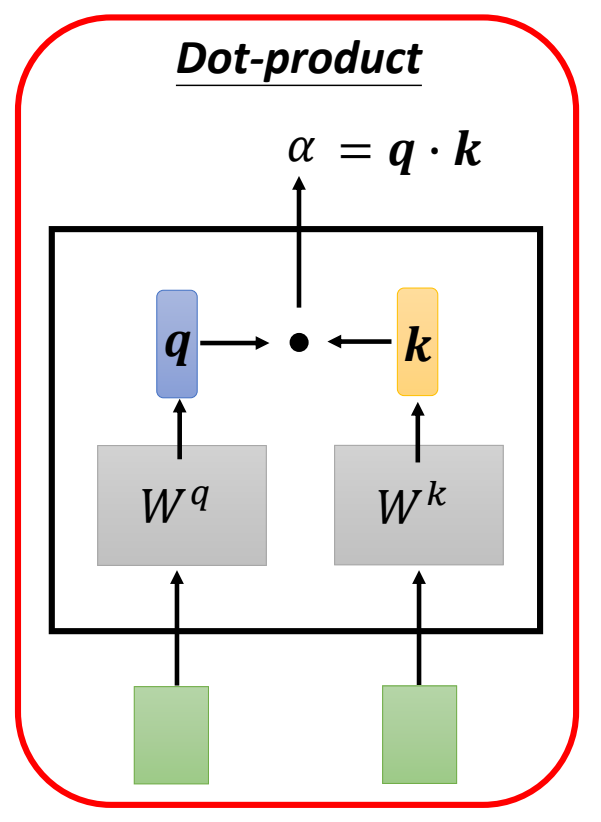
使用点乘计算\(\alpha_{1,i}\):
输入:\(a^{(1)}\)和\(a^{(i)}\)
输出:\(\alpha\)
过程:
- \(\mathbf{q} = a^{(1)}\cdot \mathrm{W}_q\):\(\mathbf{q}\)表示query,可以理解为\(a^{(1)}\)当前希望获取的信息,是\(a^{(1)}\)对\(a^{(i)}\)的“需求”。\(\mathrm{W}_q\)是待学习的参数。
- \(\mathbf{k} = a^{(i)}\cdot \mathrm{W}_k\):\(\mathbf{k}\)表示key,可以理解为\(a^{(i)}\)对query的“回答”。\(\mathrm{W}_k\)是待学习的参数。
- \(\alpha = \mathbf{q}\cdot \mathbf{k}\):\(\alpha_{1,i}\)表示\(a^{(1)}\)和\(a^{(i)}\)的相关性得分。\(\mathbf{q}\)和\(\mathbf{k}\)越接近,说明\(a^{(i)}\)的做出的回答正好是\(a^{(1)}\)所需要的,二者相关性得分也就越高。
按照上面的方法,分别计算\(a^{(1)}\) 和\(a^{(2)},a^{(3)},\cdots a^{(n)}\)的\(\alpha\)。并且计算\(a^{(1)}\)和\(a^{(1)}\)自己的\(\alpha\)。
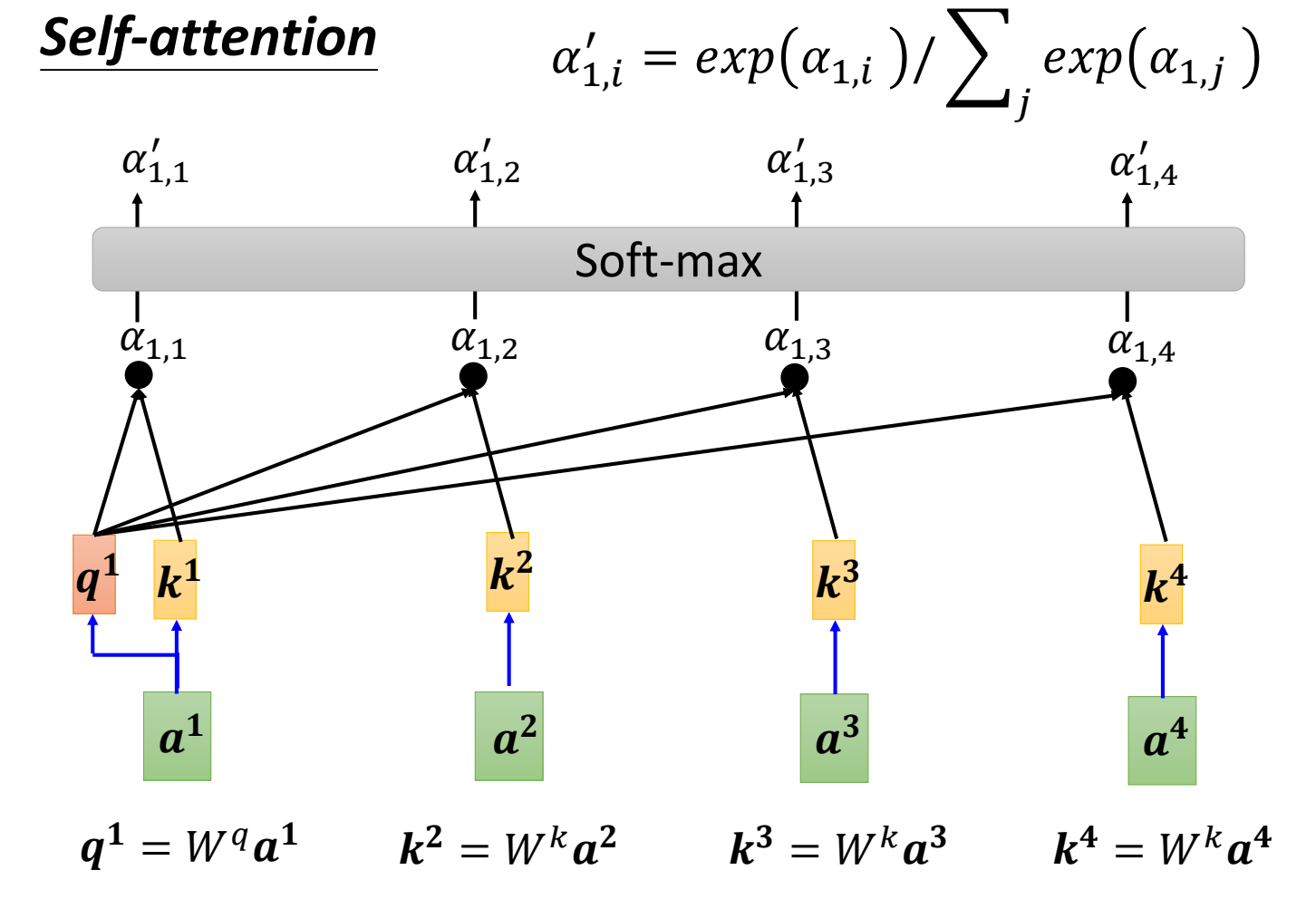
得到\(a^{(1)}\)和\(a^{(1)},a^{(2)},\cdots a^{(n)}\)的\(\alpha\)后,过一个softmax,得到\(\alpha '\)。(\(\alpha '\)叫做相关性概率)
-
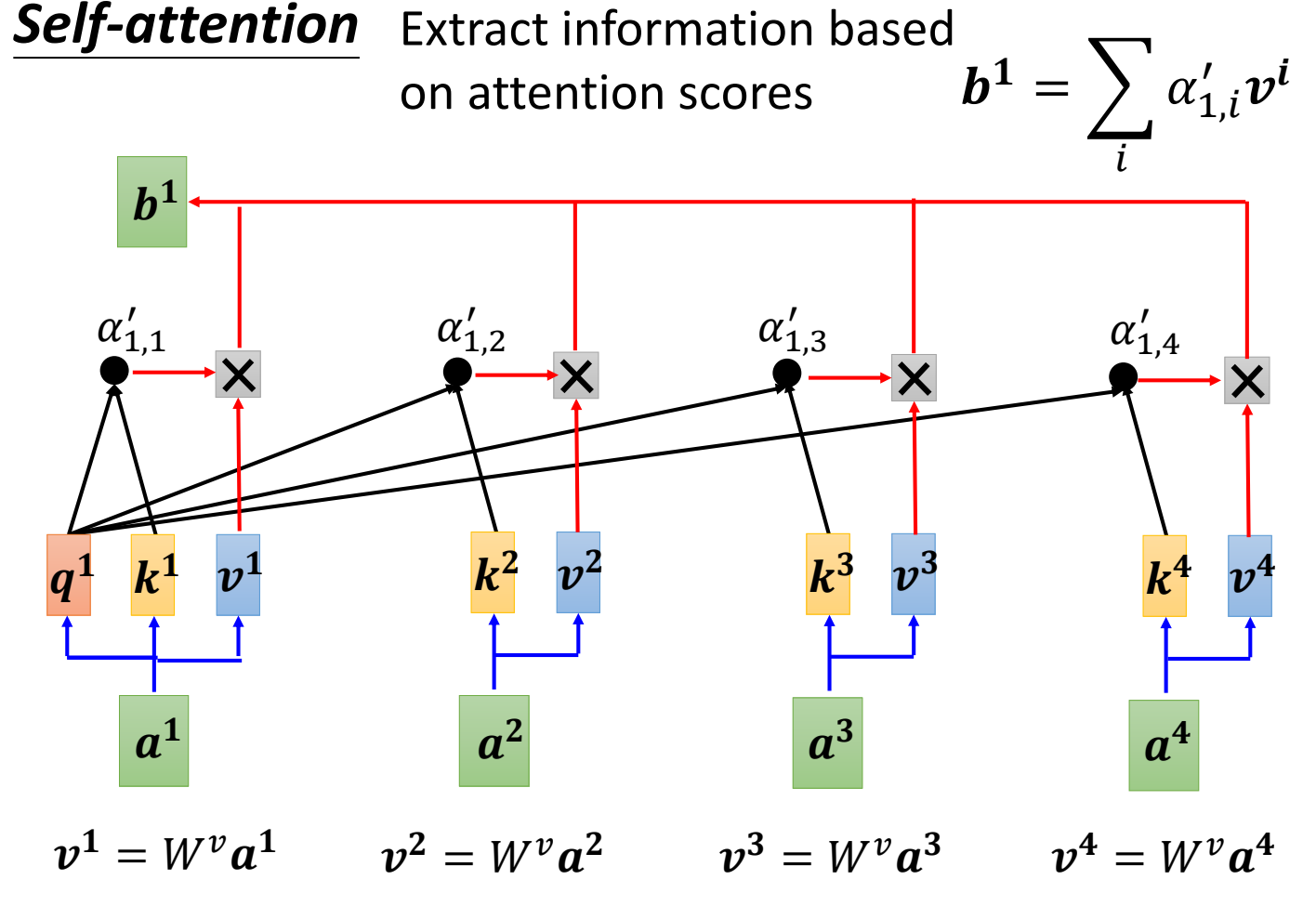
根据\(\alpha '\)来抽取重要的信息:
- \(\mathbf{v}^{(i)} = a^{(i)}\cdot W_v\):\(\mathbf{v}\)表示value。可以理解是\(a^{(i)}\)的语义信息。\(\mathrm{W}_v\)是待学习的参数。
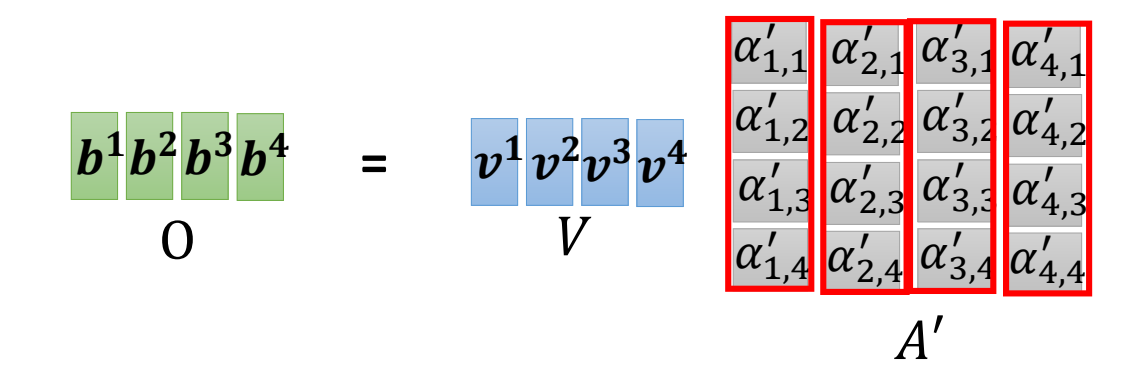
- \(b^{(1)} = \sum_i\alpha'_i\cdot v^{(i)}\):在 Attention 操作中,首先通过 query 和 key 的匹配得到相关性概率,然后从每个输入的value 中提取信息。最终结果是所有 value的加权平均,其中权重就是每个位置的相关性概率。\(b^{(1)}\)离哪个value越近,说明\(a^{(1)}\)和哪个输入越相关。
-
最后的结果\(b^{(1)}\)就是\(a^{(1)}\)经过selt-attention层后的输出。
-
3. self-attention的并行计算
需要注意的是,对于self-attention来说,不管是哪个输入,参数\(W_q,W_k,W_v\)都是相同的。因此,self-attention可以并行计算。
如下图,如果我们将所有的输入组合成矩阵\(\mathbf{I}\),那么通过矩阵运算,可以同时计算出所有输入的\(\mathbf{q},\mathbf{k},\mathbf{v}\),并把这些\(\mathbf{q},\mathbf{k},\mathbf{v}\)分别组成矩阵,记作\(Q,K,V\).
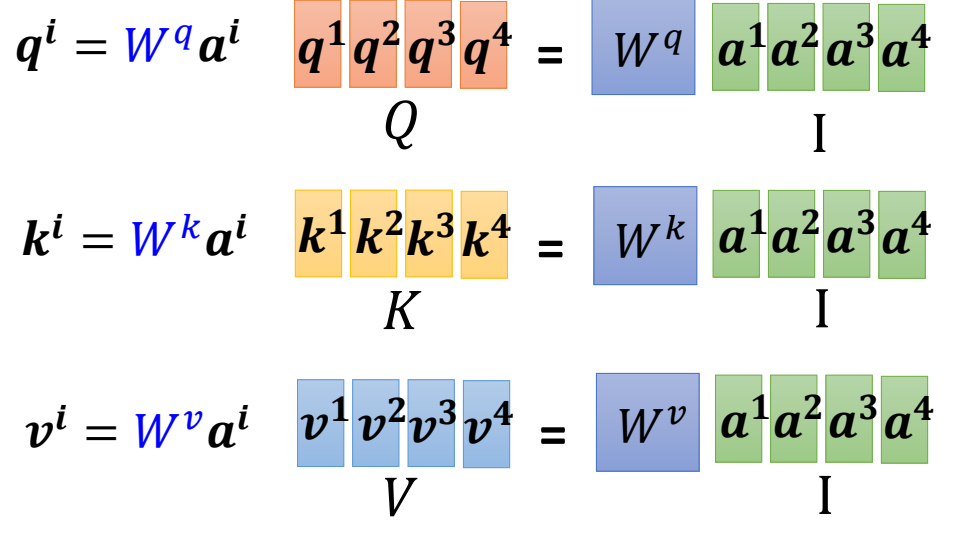
所有的\(\alpha\)和\(\alpha'\)也可以一次计算出来。

有了所有的\(\alpha'\),最终的输出也可以一次计算出来。
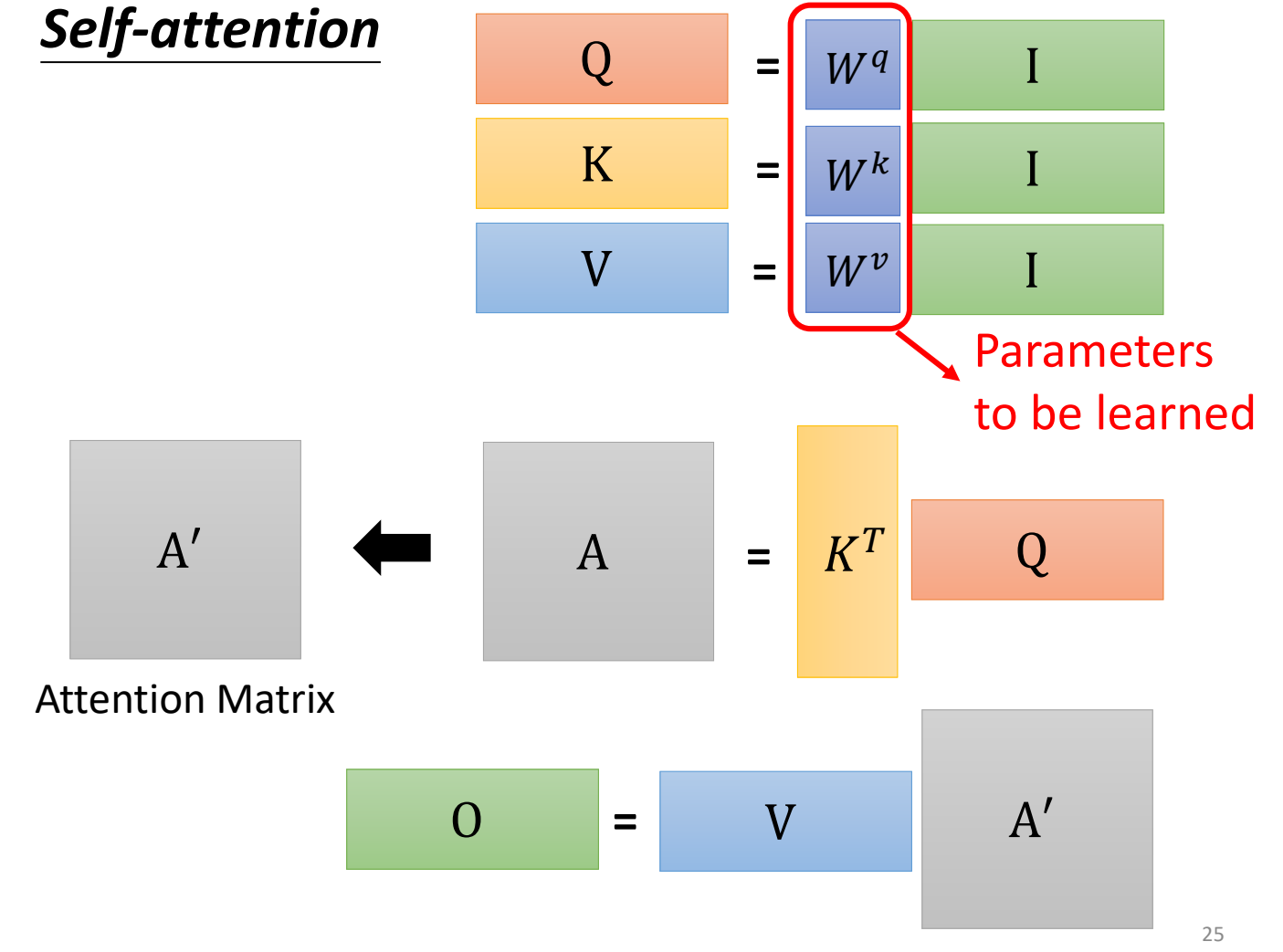
总结一下,过程如下,只要我们学习到了参数\(W_q,W_k,W_v\),那么self-attention层所有的输出可以一次计算出来。这也是为什么self-attention得到了如此广泛的应用的原因之一。
4. 多头self-attention
回忆一下卷积操作。有些时候,我们需要多个卷积核,每个卷积核负责提取不同的pattern。
self-attention也是一样,我们会需要多个self-attention,来提取不同维度的相关性。例如,对于一个人来说,可能会有性别相关,职业相关,年龄相关等等不同维度的相关性,我们想要把这个相关都找出来,就需要多个selt-attention。
这样的self-attention叫做多头self-attention。
在多头self-attention中,每个头都会独立训练出一组\(W_q,W_k,W_v\)。因此,对于输入\(a^{(i)}\)来说,每个头都会产生一个输出,记作\(b^{i,1},b^{i,2},\cdots\)
最后,额外训练一组参数\(\mathbf{w}_1,\mathbf{w}_2,\cdots\),多头self-attention层的输出为\(\mathbf{w}_1\cdot b^{i,1}+\mathbf{w_2}\cdot b^{i,2}+\cdots\)
5. 位置编码,self-attention的扩展知识
从上文中,我们可以发现self-attention没有位置信息。
但有时候, 位置信息的必要的,例如词性标记中,句子中第一个词是动词的可能性比较低。
这时候就需要位置编码了。
位置编码:对每一个位置,设置一个向量\(e^{(i)}\),每个不同的位置都有不同的\(e^{(i)}\),将\(e^{(i)}\)直接加到\(a^{(i)}\)中,就结束了。
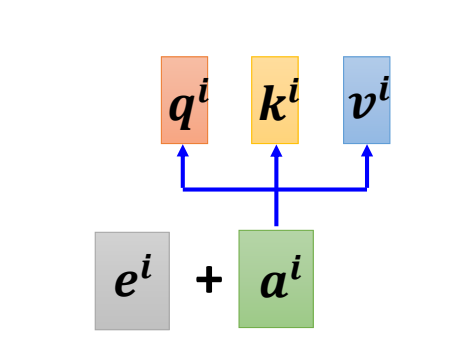
\(e^{(i)}\)长什么样子呢?
在传统的transformer中,\(e^{(i)}\)是通过sin和cos所产生的。
但是,\(e^{(i)}\)的规则不是确定的,可以使用别的规则.甚至可以使用模型来学习
-
self-attention的应用
-
transformer和BERT中,都有self-attention
-
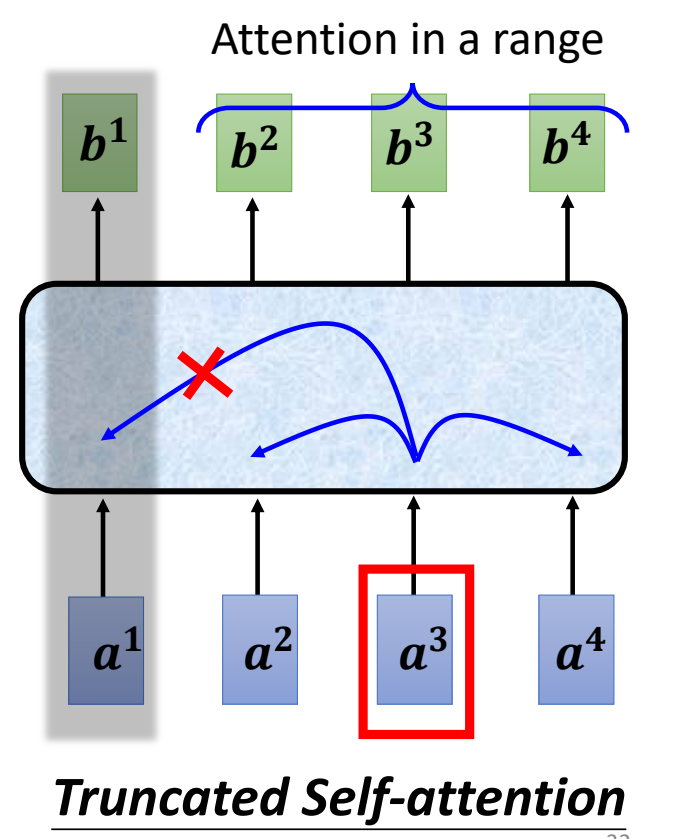
self-attention 用在语音上:一段不长的语音,可能会有很多向量。如果计算语音中所有的向量,计算量过大,因此产生了truncated self-attention : self-attention只需要关注输入前面和输入后面几个向量就行(窗口大小是人为设定的),窗口外的向量则不需要关注。
-
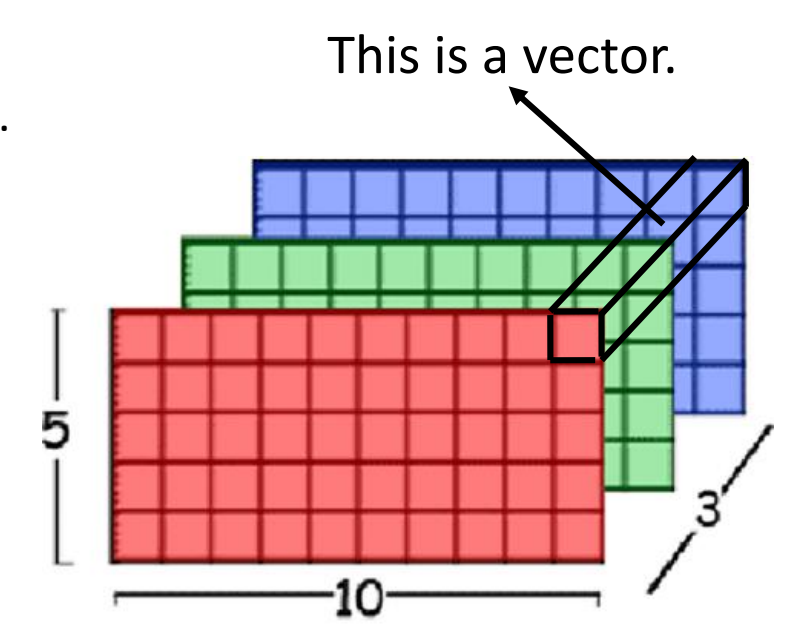
self-attention 用在图像上: 一张图片看作一个vector-set,其中一个RGB像素是三维的vector,因此图像也可以使用self-attention处理
-
-
self-attention和卷积:CNN默认,输入像素与感受野中的像素相关。而使用self-attention,模型自动找到哪个像素和输入像素相关,就好像感受野自动被学出来一样。因此,self-attention是一般化的卷积,卷积是self-attention的特例。并且,通过设置参数,self-attention也可以表示卷积。(见论文 On the Relationship between Self-Attention and Convolutional Layers)
-
self-attention和RNN:self-attention可以捕捉RNN捕捉不到的长距离的依赖。并且,self-attention可以并行计算,在性能上显著优于RNN。




