The Activation Function in Deep Learning 浅谈深度学习中的激活函数

原文地址：http://www.cnblogs.com/rgvb178/p/6055213.html
版权声明：本文为博主原创文章，未经博主允许不得转载。

激活函数的作用

首先，激活函数不是真的要去激活什么。在神经网络中，激活函数的作用是能够给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。
比如在下面的这个问题中：

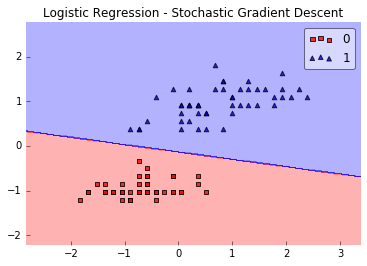
如上图(图片来源)，在最简单的情况下，数据是线性可分的，只需要一条直线就已经能够对样本进行很好地分类。

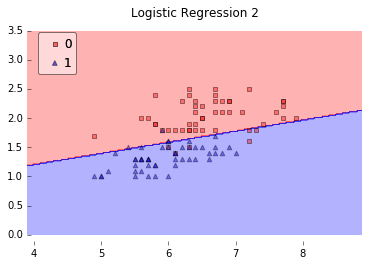
但如果情况变得复杂了一点呢？在上图中(图片来源)，数据就变成了线性不可分的情况。在这种情况下，简单的一条直线就已经不能够对样本进行很好地分类了。

于是我们尝试引入非线性的因素，对样本进行分类。

在神经网络中也类似，我们需要引入一些非线性的因素，来更好地解决复杂的问题。而激活函数恰好能够帮助我们引入非线性因素，它使得我们的神经网络能够更好地解决较为复杂的问题。

激活函数的定义及其相关概念

在ICML2016的一篇论文Noisy Activation Functions中，作者将激活函数定义为一个几乎处处可微的 h : R → R 。

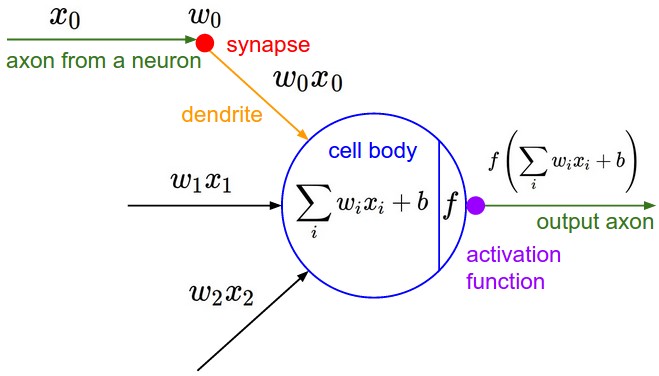
在实际应用中，我们还会涉及到以下的一些概念：
a.饱和
当一个激活函数h(x)满足$$\lim_{n\to +\infty} h'(x)=0$$时我们称之为右饱和。

当一个激活函数h(x)满足$$\lim_{n\to -\infty} h'(x)=0$$时我们称之为左饱和。当一个激活函数，既满足左饱和又满足又饱和时，我们称之为饱和。

b.硬饱和与软饱和
对任意的\(x\)，如果存在常数\(c\)，当\(x > c\)时恒有 \(h’(x) = 0\)则称其为右硬饱和，当\(x < c\)时恒 有\(h’(x)=0\)则称其为左硬饱和。若既满足左硬饱和，又满足右硬饱和，则称这种激活函数为硬饱和。但如果只有在极限状态下偏导数等于0的函数，称之为软饱和。

Sigmoid函数

Sigmoid函数曾被广泛地应用，但由于其自身的一些缺陷，现在很少被使用了。Sigmoid函数被定义为：$$f(x)=\frac{1}{1+e^{-x}}$$函数对应的图像是：

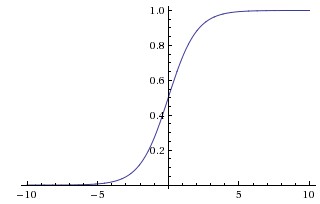
优点：
1.Sigmoid函数的输出映射在\((0,1)\)之间，单调连续，输出范围有限，优化稳定，可以用作输出层。
2.求导容易。

缺点：
1.由于其软饱和性，容易产生梯度消失，导致训练出现问题。
2.其输出并不是以0为中心的。

##tanh函数 现在，比起Sigmoid函数我们通常更倾向于tanh函数。tanh函数被定义为$$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$ 函数位于[-1, 1]区间上，对应的图像是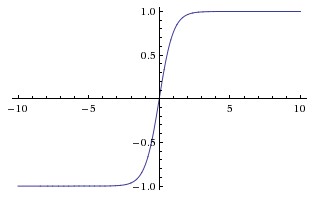：  **优点：** 1.比Sigmoid函数收敛速度更快。 2.相比Sigmoid函数，其输出以0为中心。 **缺点：** 还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失。
##ReLU ReLU是最近几年非常受欢迎的激活函数。被定义为$$y= \begin{cases} 0& (x\le0)\\ x& (x>0) \end{cases}$$对应的图像是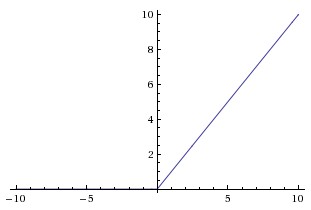：  但是除了ReLU本身的之外，TensorFlow还提供了一些相关的函数，比如定义为min(max(features, 0), 6)的tf.nn.relu6(features, name=None)；或是CReLU，即tf.nn.crelu(features, name=None)。其中(CReLU部分可以参考[这篇论文][4])。 **优点：** 1.相比起Sigmoid和tanh，ReLU[(e.g. a factor of 6 in Krizhevsky et al.)][5]在SGD中能够快速收敛。例如在下图的实验中，在一个四层的卷积神经网络中，实线代表了ReLU，虚线代表了tanh，ReLU比起tanh更快地到达了错误率0.25处。据称，这是因为它线性、非饱和的形式。 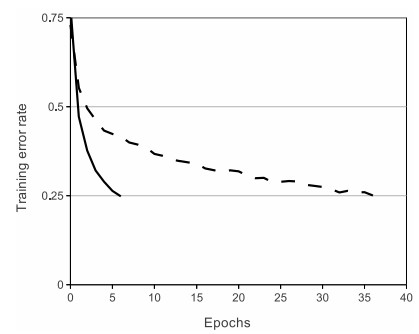 2.Sigmoid和tanh涉及了很多很expensive的操作（比如指数），ReLU可以更加简单的实现。 3.有效缓解了梯度消失的问题。 4.在没有无监督预训练的时候也能有较好的表现。 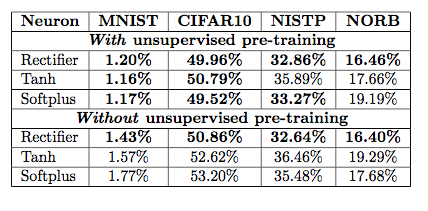 5.提供了神经网络的稀疏表达能力。

缺点：
随着训练的进行，可能会出现神经元死亡，权重无法更新的情况。如果发生这种情况，那么流经神经元的梯度从这一点开始将永远是0。也就是说，ReLU神经元在训练中不可逆地死亡了。

##LReLU、PReLU与RReLU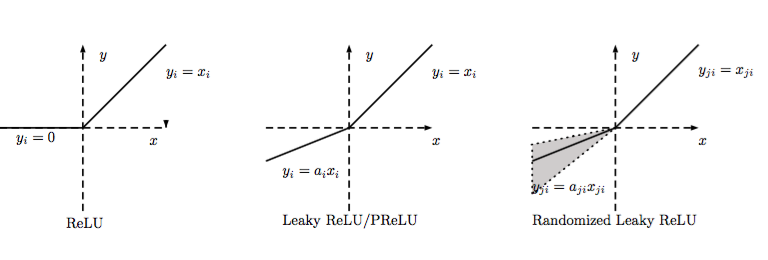 

通常在LReLU和PReLU中，我们定义一个激活函数为

\[f(y_i)=\begin{cases} y_i& if(y_i>0)\\ a_iy_i& if(y_i\le0) \end{cases}\]

-LReLU
当\(a_i\)比较小而且固定的时候，我们称之为LReLU。LReLU最初的目的是为了避免梯度消失。但在一些实验中，我们发现LReLU对准确率并没有太大的影响。很多时候，当我们想要应用LReLU时，我们必须要非常小心谨慎地重复训练，选取出合适的\(a\)，LReLU的表现出的结果才比ReLU好。因此有人提出了一种自适应地从数据中学习参数的PReLU。

-PReLU
PReLU是LReLU的改进，可以自适应地从数据中学习参数。PReLU具有收敛速度快、错误率低的特点。PReLU可以用于反向传播的训练，可以与其他层同时优化。

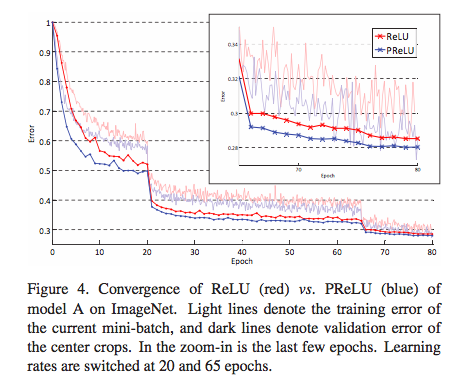
在论文Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification中，作者就对比了PReLU和ReLU在ImageNet model A的训练效果。
值得一提的是，在tflearn中有现成的LReLU和PReLU可以直接用。

-RReLU
在RReLU中，我们有$$y_{ji}=\begin{cases}
x_{ji}& if(x_{ji}>0)\
a_{ji}x_{ji}& if(x_{ji}\le0)
\end{cases}$$$$a_{ji} \sim U(l,u),l<u;;and;;l,u\in [0,1) $$
其中，\(a_{ji}\)是一个保持在给定范围内取样的随机变量，在测试中是固定的。RReLU在一定程度上能起到正则效果。

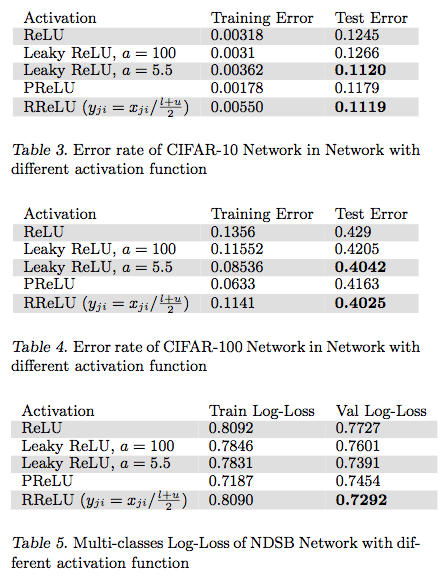
在论文Empirical Evaluation of Rectified Activations in Convolution Network中，作者对比了RReLU、LReLU、PReLU、ReLU 在CIFAR-10、CIFAR-100、NDSB网络中的效果。

ELU

ELU被定义为$$f(x)=\begin{cases}
a(e^x-1)& if(x<0)\
x& if(0\le x)
\end{cases}$$其中\(a>0\)。

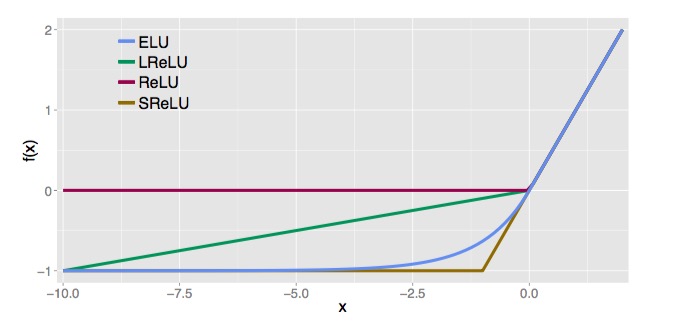
优点：
1.ELU减少了正常梯度与单位自然梯度之间的差距，从而加快了学习。
2.在负的限制条件下能够更有鲁棒性。

ELU相关部分可以参考这篇论文。

Softplus与Softsign

Softplus被定义为$$f(x)=log(e^x+1)$$
Softsign被定义为$$f(x)=\frac{x}{|x|+1}$$
目前使用的比较少，在这里就不详细讨论了。TensorFlow里也有现成的可供使用。激活函数相关TensorFlow的官方文档

##总结 关于激活函数的选取，目前还不存在定论，实践过程中更多还是需要结合实际情况，考虑不同激活函数的优缺点综合使用。同时，也期待越来越多的新想法，改进目前存在的不足。

文章部分图片或内容参考自：
CS231n Convolutional Neural Networks for Visual Recognition
Quora - What is the role of the activation function in a neural network?
深度学习中的激活函数导引
Noisy Activation Functions－ICML2016
本文为作者的个人学习笔记，转载请先声明。如有疏漏，欢迎指出，不胜感谢。