机器学习 (三) 逻辑回归 Logistic Regression
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准。感谢博主Rachel Zhang 的个人笔记,为我做个人学习笔记提供了很好的参考和榜样。
§ 3. 逻辑回归 Logistic Regression
1 分类Classification
首先引入了分类问题的概念——在分类(Classification)问题中,所需要预测的$y$是离散值。例如判断一封邮件是否属于垃圾邮件、判断一个在线交易是否属于诈骗、一个肿瘤属于良性肿瘤还是恶性肿瘤等,都属于分类问题。

对于有两种类别的分类(例如上述三个例子),可以分别将两种类别标记为正类(Positive Class)和负类(Negative Class)。在实际应用中,把一个类别标记为正类或负类是任意的,但一般来说会用正类代表拥有某样东西,用负类代表缺少某样东西。
分类问题可以分为多类分类(Multiclass Classification)问题和二元分类(Binary Classification)问题。
Andrew Ng以肿瘤分类问题为例,讲解了在分类问题中线性回归方法的有效性较低的原因。

如图,当前的数据集中,如果应用线性回归方法并以$h_{\theta}(x)=0.5$为阈值将肿瘤分类,即以$h_{\theta}(x)=0.5$在横轴上的投影点为基准进行划分,左边的预测为良性肿瘤,右边的预测为恶性肿瘤,那么预测的效果还是很不错的。

但在加入了最右的数据点之后,表示$h_{\theta}(x)$的直线从紫色线变成了蓝色线,预测准确性在$h_{\theta}(x)=0.5$处可以看出有了比较明显的降低。
如果线性回归算法应用在分类问题中,那么在y={0,1}的情况下,也有可能会出现$h_{\theta}(x)<0$或者$h_{\theta}(x)>1$的情况,而且$h_{\theta}(x)$可能会远小于0或者远大于1。因此,分类问题并不适合拿线性回归的方法来解决。
2 逻辑回归Logistic Regression
下面引入能够满足$0<=h_{\theta}(x)$的逻辑回归算法来解决上述问题。逻辑回归算法虽然名字上有个“回归”,但事实上是个分类算法。

首先引入了逻辑函数(Logistic Function),也称S型函数(Sigmoid Function)——如图中的$g(z)$所示。逻辑函数的性质是:在正无穷处无限趋近于1,在负无穷处无限趋近于0,在z=0处值为0.5。

Andrew Ng解释了$P(y=1|x;\theta)$所代表的含义,然后给出了$P(y=1|x;\theta)$与$P(y=0|x;\theta)$的重要特点——相加等于1。
然后给出了以下例题,考察了上述知识点。

3 决策边界Decision Boundary
决策边界(Decision Boundary) 将整个平面分为y=1和y=0的两个预测区域,对于$\theta^{T}x>=0$的部分,有$h_{\theta}(x)$>0.5,因此预测为y=1;对于$\theta^{T}x<0$的部分则反之,预测为y=0。
决策边界不是训练集的属性,而是假设本身及其参数的属性。一旦给定了$\theta$,那么其决策边界就已经确定了。我们不是用训练集来定义决策边界,而是用训练集来拟合参数$\theta$。

如果在平面上把训练集和决策边界都表现出来,那么应该是类似下图这样的效果。

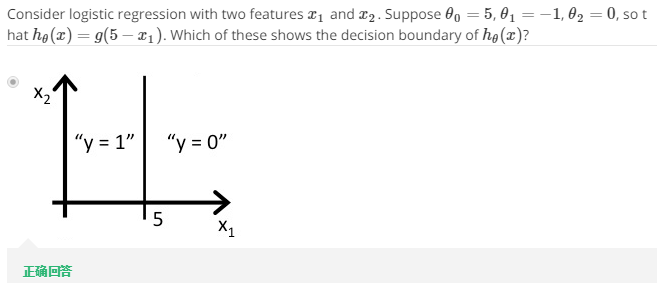
又例如下题中,$5-x_{1}=\theta^{T}x$,当$5-x_{1}=\theta^{T}x>=0$时有$x_{1}<5$,因此图像如图所示。而$x_{1}=5$即为该预测函数的决策边界。
非线性决策边界(Non-Linear decision boundaries),拥有复杂的多项式特征变量,得到复杂的决策边界,而不是简单的用直线分开正负样本。
例如如下的情况:

4 代价函数Cost Function
逻辑回归模型中的代价函数如下所示:

对于y=1:如果预测正确,那么代价为0;如果预测错误,那么代价将随着预测值趋于0而趋于无穷。即当预测错误时我们会以非常大的代价来惩罚学习算法。

对于y=0:也是类似的,$Cost=0$ if $y=1$,$h_{\theta}(x)=1$
But as $h_{\theta}(x)\rightarrow 1$ $Cost\rightarrow \infty$
Captures intuition that if $h_{\theta}(x)= 1$(predict $P(y=0|x;\theta)=0$),but y=0,we will penalize learning algorithm by a very large cost.

5 简化代价函数与梯度下降算法Simplified cost function and gradient descent
因为y只有两个取值:0,1
所以可以简化代价函数为:

接下来,我们的目标就是最小化参数$\theta$了。

之前提到过梯度下降算法,这里也是类似的用法:

代入上述蓝色式子可得

这个算法看起来似乎与应用于线性回归的梯度下降算法是一样的,但是事实上,这个式子中$h_{\theta}(x)$的假设并不同于应用于线性回归的梯度下降算法中的$h_{\theta}(x)$。
特征缩放也适用于逻辑回归算法中使得收敛速度更快。
6 高级优化算法Advanced Optimization
除了梯度下降算法之外,还可以考虑以下三种算法。这三种算法的有点是不用手动选择$\alpha$、速度快,但也相应来说更复杂。
在算法实现的过程中,建议尽量调用matlab或者octave中已有的库。

例如:

一般来说,我们可以使用octave中的fminunc来实现这一算法,但是在fminunc中,$\theta$的维数应该大于1.
下面来看具体的实现:
1 function [jVal,gradient] = costFunction(theta) 2 % jVal is how we will compute the cost function J 3 % a vector,the elements of the gradient vector correspond to partial derivative terms 4 5 jVal = (theta(1)-5)^2+(theta(2)-5)^2; 6 7 gradient = zeros(2,1); 8 gradient(1) = 2*(theta(1)-5); 9 gradient(2) = 2*(theta(2)-5);
上述代码可以保存为costFunction.m然后在matlab里面调用
1 options = optimset('GradObj','on','MaxIter',100); 2 %'GradObj','on' ->sets the gradientobjective parameter to on 3 % so you will provide a gradient to this algorithm 4 %'MaxIter',100 -> sets maximum number of iterations to 100 5 % so you will give it an initial guess for theta 6 7 initialTheta = zeros(2,1); 8 9 [optTheta,functionVal,exitFlag] = fminunc(@costFunction,initialTheta,options) 10 %fminunc is the advanced optimization
与Andrew Ng原slide所不同的地方是,原文的迭代次数设置为了'100',但其实'100'代表的是一个字符串,因此应该直接设置为100。
可得结果:
initialTheta =
0
0
Local minimum found. Optimization completed because the size of the gradient is less than the default value of the function tolerance. <stopping criteria details> optTheta = 5 5 functionVal = 0 exitFlag = 1
7 多类分类问题 Multiclass Classification
多类分类问题 Multiclass Classification是指有两个以上分类的分类问题。
在多类分类问题里,其实是产生了多个分类器的。
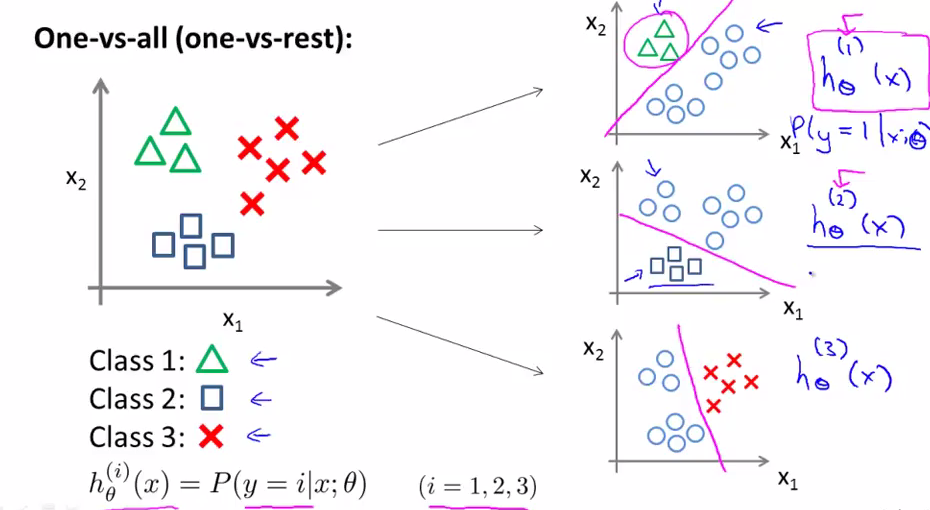
这样one-vs-all的方法中,实际上由每个分类i的所有可能结果y=i来训练逻辑回归分类器。

然后选择一个让h最大的i,不论i为多少我们都有最高的概率值。

笔记目录
(一)单变量线性回归 Linear Regression with One Variable
(二)多变量线性回归 Linear Regression with Multiple Variables
(四)正则化与过拟合问题 Regularization/The Problem of Overfitting
(五)神经网络的表示 Neural Networks:Representation
(六)神经网络的学习 Neural Networks:Learning
(七)机器学习应用建议 Advice for Applying Machine Learning
(八)机器学习系统设计Machine Learning System Design
(九)支持向量机Support Vector Machines
(十)无监督学习Unsupervised Learning
(十一)降维 Dimensionality Reduction
(十二)异常检测Anomaly Detection
(十三)推荐系统Recommender Systems
(十四)大规模机器学习Large Scale Machine Learning



 浙公网安备 33010602011771号
浙公网安备 33010602011771号