机器学习算法--贝叶斯分类器（一）

该文章参考周志华老师著的《机器学习》一书

 

1. 贝叶斯决策论

 

   定义： 贝叶斯决策论是概率框架下实施决策的基本方法。对分类任务来说，在所有概率都已知的理想情形下，贝叶斯决策考虑如何基于这些概率和误判损失来选择最优的类别标记，下面以多分类任务为例来解释其基本原理。

 

   条件风险：假设有N中可能的类别标记，即 Y={c₁,c₂,...,c_N}, λ_ij 是将一个真实标记为 c_j 的样本误分类为 c_i 所产生的损失。基于后验概率 P(c_i|x) 可获得样本x分类为c_i所产生的期望损失，即在样本x上的“条件风险”

   这是单个样本的条件风险，若对每个样本的风险最小化了，那么所有样本的总体风险也将被最小化，这就产生了贝叶斯判定准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险 R(c_i|x) 最小的类别标记，即

 

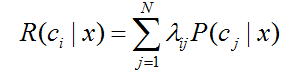
   注：此时h*称为贝叶斯最优分类器，与之对应的总体风险R(h*)称为贝叶斯风险，当风险最小的时候，分类器的性能达到最好。

 

 

   具体来说，若目标是最小化分类错误率，则误判损失 λ_ij 可写为：

 

 

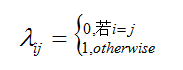
  此时条件风险 R(c|x)=1-P(c|x)，于是最小化分类错误率的贝叶斯最优分类器为

 

  即对每个样本x，选择能使后验概率P(c|x)最大的类别标记。

 

    欲使用贝叶斯判定准则来最小化决策风险，首先要获得后验概率 P(c|x)，然而在现实生活中是很难直接获得的。从这个角度来看，机器学习所要实现的是基于有限的训练样本尽可能准确地估计出后验概率 P(c|x).大体来说，有两种策略：

（1）给定x，直接建模 P(c|x)来预测 c，这样得到“判别式模型”；

（2）先对联合概率P(x,c)建模，再由此得到 P(c|x)，得到的是“生成式模型”（注：决策树、BP神经网络、支持向量机等都可归入判别式模型的范畴）。对于生成式模型来说，考虑

 

 

  注：P(c)是“先验”概率；P(x|c)是样本 x 相对于类标记 c 的类条件概率，或称为“似然”；P(x) 是归一化的因子。给定样本 x，P(x) 与类标记无关，

  因此估计 P(c|x) 问题就转化为如何基于训练数据 D 来估计先验 P(x) 和似然 P(x|c)，P(c) 可通过各类样本出现的频率来进行估计，而类条件概率不能直接估计，一种常用策略是极大似然估计法。