真真假假分不清——浅谈 2-SAT
关于 SAT
SAT 问题是适定性(Satisfiability)问题的简称。中文是所谓的 k-适定性问题,也就是 k-SAT。
这种问题的定义非常简单:
给定布尔变量集合,每个变量只能赋值为真假,要求对每个变量赋值满足一个布尔方程。
可能比较抽象,其实可以理解为有 bool 变量的集合 \(\mathbb B=\{a_1,a_2,a_3,\dots,a_n\}\)
要求求出
这样形式的一个方程的解。
实际上,虽然集合元素达到有 \(n\) 个之多,但是我们的限制条件,也就是所谓的括号内单个的布尔方程不一定会关系到整个集合的所有元素。我们假设对于每一个括号内独立的方程存在一个布尔集合映射 \(\mathbb S_i\in\mathbb B\)。那么如果这些子集的元素个数都为 \(k\)(每个 clause 选取 \(k\) 个变量),那么我们认为这就构成了一个 \(k\) 适定性问题。
没有理解没有关系,因为 k-SAT 不考(雾)。
对于这样一个问题,我们显然可以暴力赋值解决。
而且当这个问题的 \(k\) 满足 \(k\geq 3\) 时,被证明为一个 NP-Complete 问题,只能暴力解决。
但是当 \(k=2\) 时,也就是对应方程组中的每一个方程只为二元方程时,我们称之为 2-SAT 问题,这类问题是可以构建模型利用 \(\texttt{Tarjan}\) 算法在线性时间内解决的。
怎么解决 2-SAT
问题转化
之前没有理解 k-SAT 没有关系,我们现在以一种通俗的方式重新定义 2-SAT 问题。
对于每个变量我们将其看作一个集合 \(\mathbb A_i=\{\texttt{true,false}\}\)。给定若干个矛盾关系 \(<a,b>\) 表示 \(a,b\) 元素矛盾(\(a,b\) 来自不同集合)。现在要求求出一种可行解使得每个集合只选择一个元素(共 \(n\) 个)且这些元素之间互无矛盾关系。
我们发现这类问题也可以通过列前文所述的布尔方程组解决。
模型建立
对于这类问题,我们不难想到建立图论模型解决。
两两布尔变量间的逻辑关系可以有多种,但实际上我们可以在 2-SAT 问题中将他们规约成 3 种关系。
- \(\neg a\or b\)
- \(a\or b\)
- \(\neg a\or \neg b\)
对于我们的 \(\or\) 运算,我们容易得到如果左边不成立则右边必须成立。所以对于 \(a,b,\neg a,\neg b\) 的状态我们用四个不同节点 \(T_a,T_b,F_a,F_b\) 表示。
对于第一个式子,当选取 \(a\) 时我们必须选 \(b\),如果选取 \(\neg b\) 时则必须选取 \(\neg a\)
下面两式同理。
所以现在我们得到一种依赖关系,可以建图了。
| \(\neg a\or b\) | \(T_a\rightarrow T_a,F_b\rightarrow F_a\) |
|---|---|
| \(a\or b\) | \(F_a\rightarrow T_b,F_b\rightarrow T_a\) |
| \(\neg a\or \neg b\) | \(T_a\rightarrow F_b,T_b\rightarrow F_b\) |
现在假设我们有依赖关系 \((\neg a\or \neg b)\and(\neg c\or a)\and(c\or\neg b)\)
依照上面方法我们可以得到
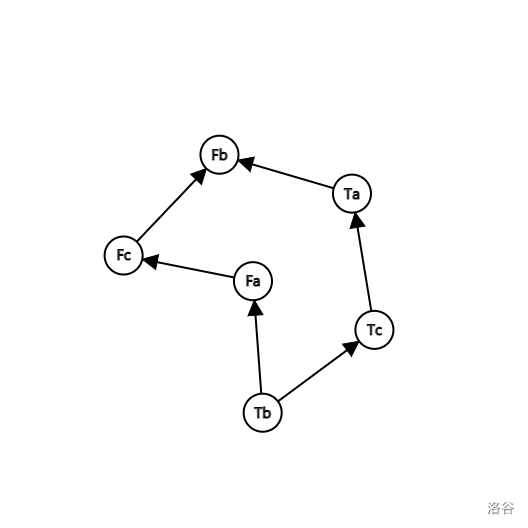
这样的一个图。
我们观察发现,这个图并非连通的有向图。所以对于每个点的情况都可以找到对应的依赖,也就是说,他是有解的。
如果我们给出一个明显的无解的依赖关系:\((\neg a\or b)\and(\neg a\or\neg b)\and(a\or b)\and(a\or \neg b)\)
我们构建出来的图长这样:
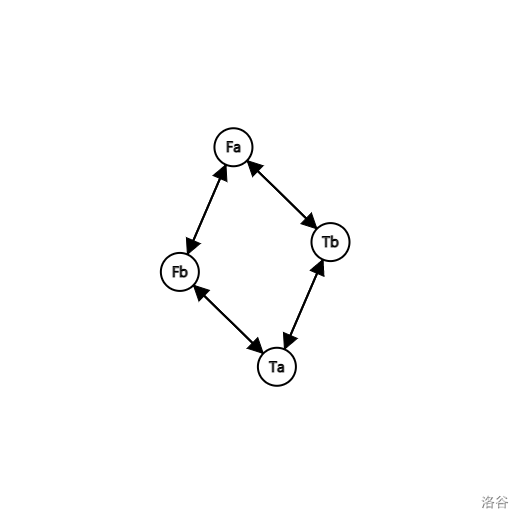
我们发现,对于一个变量 \(a\) 或 \(b\),他们的其中一值的依赖对象可以达到另一个取值。这样就会出现无解的情况。其实这是一个很容易去感谢理解的点。毕竟当对于一个布尔变量要求到其取 \(2\) 个值的时候,就一定是无解。
那么转换一下我们发现,当一个变量的 \(2\) 个逻辑值的代表节点在同一个强连通分量时,这个 2-SAT 问题就是无解的。
寻找方案
其实模型建立出来了,找方案只需要一句话即可。
我们可以通过判断每个点 \(2\) 个取值节点所在的强连通分量的拓扑序即可。
由于拓扑序靠后必然不影响拓扑序靠前的节点,所以对于每个变量我们选择拓扑序更大的节点对应的逻辑值。
不过对于 \(\texttt{Tarjan}\) 来说,由于栈的使用,拓扑序顺序是相反的,实现时需要注意,不过一般来说自己通过样例试验一下哪个是对的即可。
实现
参考模板题 Luogu P4782 【模板】2-SAT 问题
#include<bits/stdc++.h>
#define INL inline
#define ll long long
#define ull unsigned long long
INL int read()
{
int x=0,w=1;char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')ch=getchar(),w=-1;
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+ch-48,ch=getchar();
return x*w;
}
const int N=1e6+5;
struct Rey{int nxt,to;}e[N<<1];
int head[N<<1],cnt;
INL void add(int u,int v)
{
e[++cnt].nxt=head[u];
e[cnt].to=v;
head[u]=cnt;
}
int dfn[N<<1],low[N<<1],col[N<<1],secs,tot;
int n,m;
bool in_stk[N<<1];
std::stack <int> stk;
INL void Tarjan(int x)
{
dfn[x]=low[x]=++tot;
stk.push(x);
in_stk[x]=1;
for(int i=head[x];i;i=e[i].nxt)
{
int v=e[i].to;
if(!dfn[v])
{
Tarjan(v);
low[x]=std::min(low[x],low[v]);
}
else
if(in_stk[v])
low[x]=std::min(low[x],dfn[v]);
}
if(dfn[x]==low[x])
{
secs++;
int tp;
do
{
tp=stk.top();
stk.pop();
in_stk[tp]=0;
col[tp]=secs;
}while(tp!=x);
}
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
n=read(),m=read();
for(int i=1,u,v,a,b;i<=m;i++)
{
u=read(),a=read(),v=read(),b=read();
if(!a&&!b){add(u+n,v);add(v+n,u);}
else if(!a&&b){add(u+n,v+n);add(v,u);}
else if(!b&&a){add(u,v);add(v+n,u+n);}
else if(a&&b){add(u,v+n);add(v,u+n);}
}
n<<=1;
for(int i=1;i<=n;i++)if(!dfn[i])Tarjan(i);
n>>=1;
for(int i=1;i<=n;i++)if(col[i]==col[i+n]){puts("IMPOSSIBLE");return 0;}
puts("POSSIBLE");
for(int i=1;i<=n;i++)
if(col[i]>col[i+n])
printf("1 ");
else
printf("0 ");
return 0;
}
彩蛋:

Reference:
- \(\text{Anguei}\) - 题解 P4782 【【模板】2-SAT 问题】


 浙公网安备 33010602011771号
浙公网安备 33010602011771号