数学(6)——一道概率期望题引发的对多维“球”体体积的讨论
Problem
Alice 在投掷飞镖,每次飞镖等概率地落在 \(x,y\in[-1,1]\) 的正方形内一点,初始靶子是一个单位圆。
每次 Alice 投掷后,如果飞镖不在靶内,则结束游戏,否则设飞镖落在点 \(P\),过 \(P\) 做垂直于 \(OP\) 的弦,新的靶子以这条弦长为直径,圆心仍是原点。
求 Alice 的期望投掷次数。
Solution
设步数 \(step=s,s\in \N_+\)
讨论 \(P(s>x)\) 的情况
约定投第 \(i\) 步时圆盘的半径是 \(r_i\),投中的坐标是 \((x_i,y_i)\),投中坐标距离圆心 \(O\) 的距离为 \(l_i=\sqrt{x_i^2+y_i^2}\)。
让一次投射成功可以继续下一次的条件其实就是 \(l_i<r_i\);
投射到任意点的概率在 \(2\times 2\) 正方形范围内是均匀分布的。
那么每次投射进入盘中的概率则是 \(\displaystyle\frac{\pi r_i^2}{2\times2}\)。
显然必然有一步,不论第一次是否出界
\(\therefore P(s>0)=1\)
如果第一次没投出,就会得到 \(P(s>1)\) 的情况。
对于第一次投后:
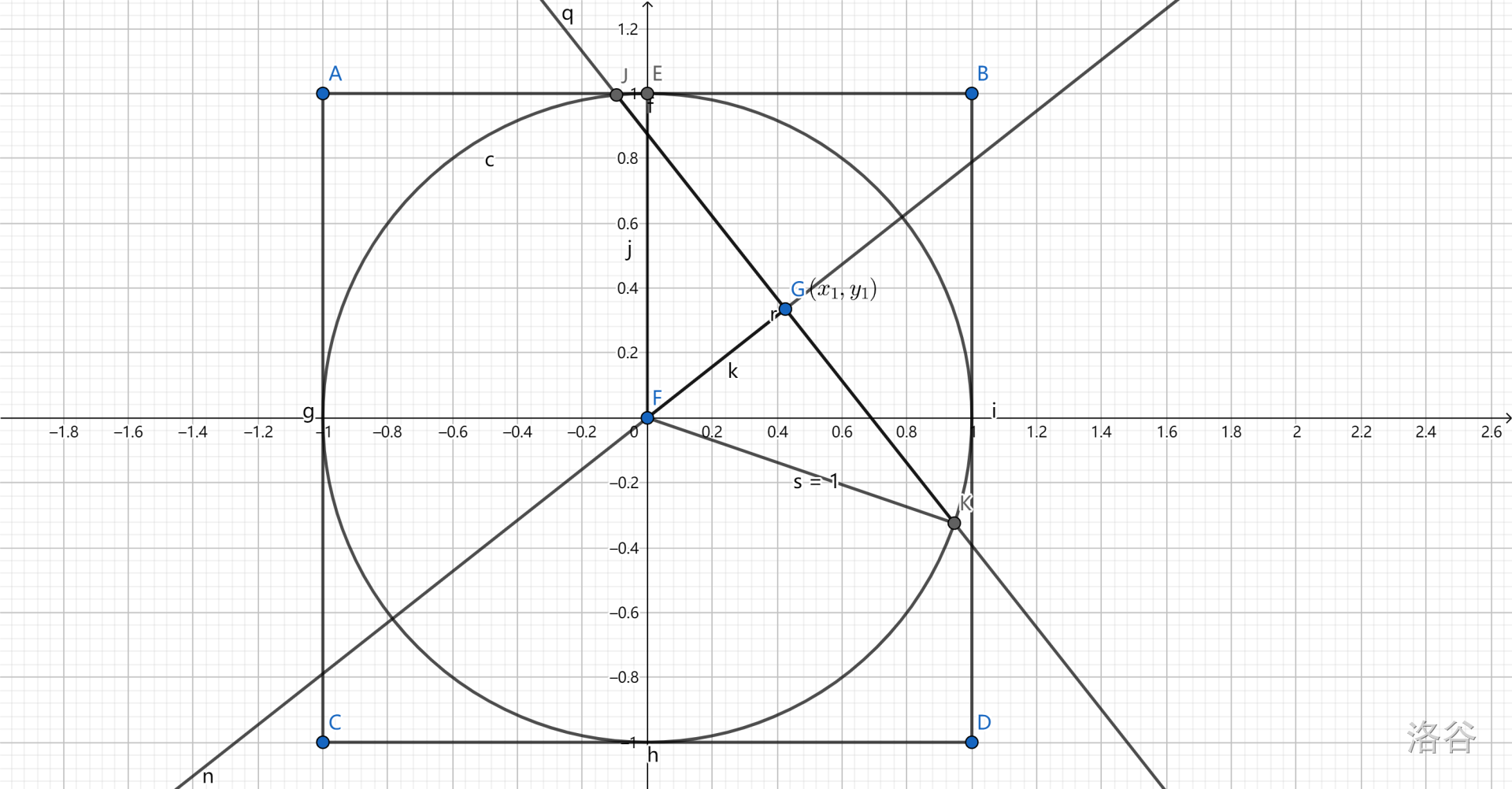
(因为作图软件的原因,我们原点 \(O\) 用 \(F\) 代替)
我们设 \(G\) 为投中的一点且在盘内,坐标为 \((x_1,y_1)\) ,我们有 \(l_1=GF=\sqrt{x_1^2+y_1^2}\)。根据游戏规则作出上图。有 \(GF\) 是新的半径。根据定义又有 \(FG \perp GK\)。
\(\therefore GK^2+GF^2=FK^2=1\)
\(r_2=GK=\sqrt{1-l_1^2}=\sqrt{1-(x_1^2+y_1^2)}\) 这里有先决条件 \(l_1<1\) 所以是实数范围内有解的。
第一次投在盘内的概率,也就是 \(P(s>1)=\displaystyle\frac{\pi}{2\times2}\)。
我们以 \(r_2\) 为新的半径,\(F\) 继续为圆心重新划分准备开始新的投射:
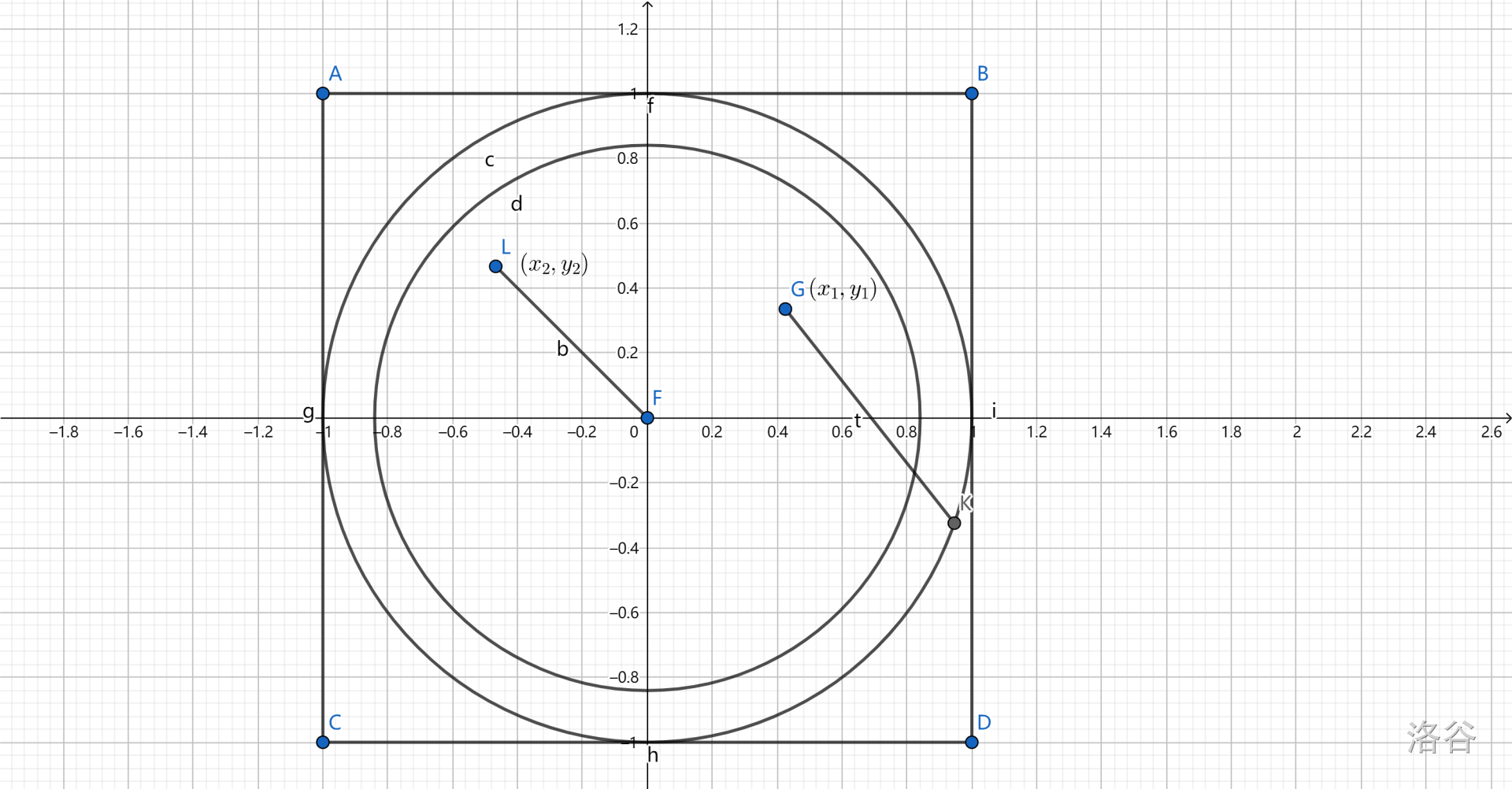
首先有 \(l_2=\sqrt{x_2^2+y_2^2}\)。
那么我们还可以继续进行游戏,也就是 \(s>2\) 的条件其实就是 \(r_2>l_2\)。
于是有 \(\sqrt{1-(x_1^2+y_1^2)}>\sqrt{x_2^2+y_2^2}\)。
两边平方,展开移项后有 \(x_1^2+y_1^2+x_2^2+y_2^2<1\)。
接下来是最巧妙的转化,也是我在查阅无数资料,向很多人请教后得出的转化。
问题现在就是我们随机选择了 \(4\) 个数 \(x_1,x_2,y_1,y_2\in[-1,1]\)(因为 \(2\) 次的投射点都是随机的),让它们平方的和小于 \(1\) 的概率是多少。
我们把这四个数建立起联系,其实就是把它们看作一个 \(\texttt{4-dimensional space point}\Rightarrow (x_1,y_1,x_2,y_2)\) 。
我们现在再从二维类推,推到三维直至四维。
我们在求 \(2\) 个随机数平方和 \(<1\) 时,会用到圆的面积公式,因为这就相当于整个范围是 \(2\times 2\) 的正方形但是点要投在在一个单位圆内。也就是 \(P(s>1)\) 的情况
类推到三维是一样的,我们有随机数 \(x,y,z\) 要求满足 \(x^2+y^2+z^2<1\) 的概率,再根据游戏规则类推,现在问题其实是,相当于总范围为一个 \(2\times 2\times 2\) 立方体(\(x,y,z\in[-1,1]\))。点要在一个单位球内。球的体积公式是 \(\displaystyle\frac43\pi r^3\) 又有 \(r=1\) 所以球体积是 \(\displaystyle\frac 4 3 \pi\)。因为在三维空间中肯定也是均匀分布,那么现在投在单位圆内的概率就是 \(\displaystyle \frac{\displaystyle \frac 4 3 \pi}{2\times 2\times 2=2^3}=\frac{\pi}{6}\)。
四维咋类推呢。我们约定一下,四维中相当于三维中体积的定义就叫“体体积”。
四维”正方体“比较显然,其”体体积”就是 \(2\times 2 \times 2\times 2\)。
那么对于四维单位“球”的“体体积”这个东西在我查阅资料后发现其值为 \(\displaystyle\frac{\pi^2}{2}r^4\)。
这个题中我们基本上先是一直考虑 \(r=1\) 的情况。所以先不管 \(r\) 吧。
观察式子发现比较有趣,因为多出来一个 \(\pi\),我们大胆猜想,这个东西应该是会在偶数位增加一个 \(\pi\)。
那么先总结一下 \(P(s>2)=\displaystyle\frac{\pi^2}{2^4\times 2}\)
在题目中每做一次投射会多出一对 \(x_i,y_i\) 也就是上面那个不等式项数会不断增加 \(2\)。但是右边的 \(1\) 永远不变,不信自己推一下吧。
所以三次后也就是 \(P(s>3)\) 的情况我们进入到 \(6\) 维坐标点 \((x_1,y_1,x_2,y_2,x_3,y_3)\)。哦,发现果然是只跟偶数维度有关系!
现在我们去 \(\texttt{Wikipedia}\) 找到了高维球体“体体体体。。。积”公式的表格!!!
长这样:
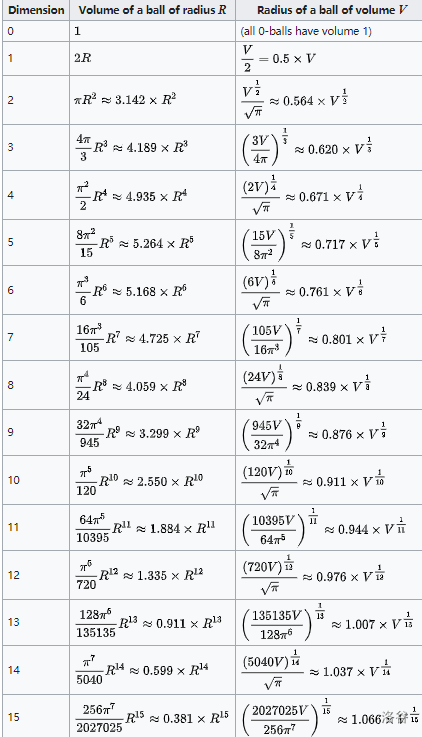
带入六维的公式,步骤与上同理。
所以 \(P(s>3)=\displaystyle\frac{\pi^3}{2^6\times6}\)
我们继续类推,通过规律找到一个通项公式:\(P(s>n)=\displaystyle\frac{\pi^n}{2^{2n}\times n!}=\displaystyle\frac{\pi^n}{4^n\times n!}\)
带入我们最开始算出的那个期望式子:\(E(s)=1+P(s>1)+P(s>2)+P(s>3)+\dots\)
我们现在有 \(E(s)=1+\displaystyle\frac{\pi}{4}+\displaystyle\frac{\pi^2}{4^2}\times\frac{1}{2!}+\displaystyle\frac{\pi^3}{4^3}\times\frac{1}{3!}\dots\)
但是,这咋找规律啊,又遇到瓶颈了。
于是我们继续去翻阅资料,突然灵光乍现!
我们忘记了除了 \(\pi\) 的另一个著名无理数 \(e\)。
这个 \(e\) 的泰勒展开公式有关于指数函数的公式:\(e^x=\displaystyle\sum_{n=0}^{\infty}\frac{x^n}{n!}\)。
对于这个题我们如果写成:\(E(s)=1+\displaystyle\frac{\pi}{4}+\frac{\displaystyle(\frac{\pi}{4})^2}{2!}+\frac{\displaystyle(\frac{\pi}{4})^3}{3!}\dots\)
发现他可以带入这个泰勒展开公式:
\(E(s)=\displaystyle\sum_{n=0}^{\infty}\frac{\displaystyle(\frac{\pi}{4})^n}{n!}=e^{\frac{\pi}{4}}\)
估算一下这个 \(e^{\frac{\pi}{4}}\approx 2.1932800507380154565597696592787\)
我们进一步用这样一个 python3 程序验证一下:
import random
import math
s=0
t=0
ans=0
count=0
while(1):
while(count<100000000):
s=0
d=1.0
w=1.0
x=0.0
y=0.0
count=count+1
t=t+1
while(1):
a=random.randint(0,1000000000)
x=float(a)/1000000000
a=random.randint(0,1000000000)
y=float(a)/1000000000
s=s+1
if x*x+y*y-d*d>0:
break
h=x*x+y*y
w=d
d=math.sqrt(w*w-h)
ans=ans+s
q=float(ans)/float(t)
print(q)
发现就是这个近似值。
这就是 \(\texttt{Mathematical exploration}\) 吗,爱了爱了。
有一个微分方程的解法,设一个概率密度函数也可以做,不多做探讨。
可以发现我们这种做法没有什么非常超纲的知识点,所以说是一道非常巧妙的题目。
Extra
我们可能还会对高维球体体积公式有一些疑惑,毕竟高维实在太难去理解了。
那我们尝试证明一下:
我们设 \(V_k(r)\) 为 \(k\) 维半径为 \(r\) 的球体体积。
首先显然对于任何一个维度有 \(V_k(r)\propto r^k\)
归纳证明即可,
我们将第 \(k\) 维球体拆分成 \(k-1\) 维的球体:
又有:
于是可以得到 \(V_{2k}(r)=\displaystyle\frac{\pi^kr^{2k}}{k!}\)
证毕。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号