题解 CF1453E 【Dog Snacks】
-
CF1453E Dog Snacks
简单树形 \(dp\) 。
-
Prelude
往树形 \(dp\) 直接想就可以了,因为我们发现既然要走完所有点,那么很显然是每个节点的子树内部跑完才会去跑别的子树。现在只需要考虑怎么走 \(k\) 最小。
-
Solution
观察这么一种情况:
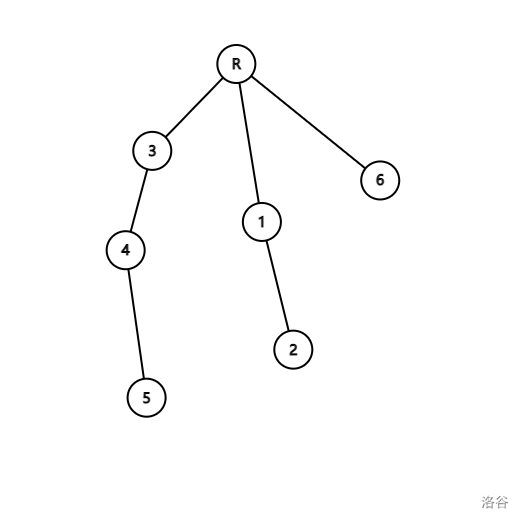
我们发现,无论先从哪个子节点下去,貌似得到的 \(k\) 都会是最长链的长度,因为你肯定要从那个最深的叶子节点回到 \(R\) 。
但是如果我们把这颗子树接到另一种情况上。
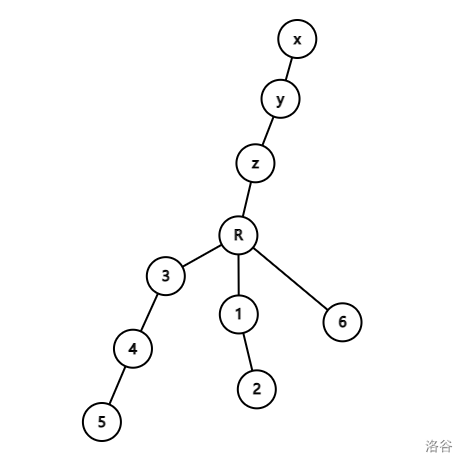
因为我们一定是从根走到子树上的节点,我们走”进去“的时候其实是无所谓的,因为都是没有走过的节点,所以最近的距离为 \(1\) 的都可以走。
于是我们只需要考率回来的操作,因为刚才那个情况全是链,所以感觉怎么走好像都无所谓啊,但是如果我们在子树的根上面接的是唯一的一条很长链,显然这上面的点都被走过了,所以每走一步都会危及到 \(k\) 的大小。我们发现从一个叶子节点走回去的路径也是一条链,是这颗子树上的一条链接上上面那条长链。对于上面那个情况我们最后直接就可以从 \(6\) 走到 \(x\) ,如果从 \(5\) 走回 \(x\) 显然很劣。
那么就很显然了,我们只需要在最后一次回来的时候走最短的链。那么策略就是每次从最长的向下走,保证最后走回来的是那条最短。也就是回去的路程一般考虑 \(\min+1\) 。
但是在子树间转移时,我们答案会不可避免地变成 \(\max+1\) 。
所以我们其实一直在考虑 \(2\) 个问题:回去的路程 \(\min+1\) 和 子树转移的路程 \(\max+1\)
我们记录状态 \(f_i\) 为距离子树中最近叶子节点的距离。
所以每次向上跳的时候,我们考虑用不同子树的最小链合并状态。那就是:
途中我们还需要记录答案,答案就是所有子树状态最大值 \(+1\) ,因为根据第一张图,而且我们要回到上一个节点,所以是最大值 \(+1\) 。
但是我们只有在一个节点有多个子树才会更新这个答案。
但是这样的话我们会发现一个问题,那就是如果上面那个子树全是链的图这样做答案是不对的。
我们发现,根节点是不需要遵从这个规律的,因为最后一次回到根节点我们就没有再下去的操作了。
什么意思呢,就是说,我们从一个子树回到父亲节点很显然要继续走这个父亲节点的其他子树,或者跳到上面去,但是根节点的最后一次不需要,也就是说我们没有子树转移的路程可以考虑,我们可以记录下次大链 \(+1\) ,其等效于子树转移的路程,这样也可以在根节点求最优了。
-
Code
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#define INL inline
using namespace std;
INL int read()
{
int x=0,w=1;char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+ch-48,ch=getchar();
return x*w;
}
const int N=4e5+5;
struct Rey
{
int nxt,to;
}e[N<<1];
int n,head[N],cnt;
int f[N],ans;
INL void add(int u,int v)
{
e[++cnt].nxt=head[u];
e[cnt].to=v;
head[u]=cnt;
}
void dfs(int x,int fa)
{
int mxn,sec_mxn,tot;
mxn=sec_mxn=tot=0;
for(int i=head[x];i;i=e[i].nxt)
{
int go=e[i].to;
if(go==fa)continue;
dfs(go,x);
tot++;//记录子树个数
f[x]=min(f[x],f[go]+1);
if(f[go]+1>mxn)sec_mxn=mxn,mxn=f[go]+1;
else if(f[go]+1>sec_mxn)sec_mxn=f[go]+1;//次大,给根转移用
}
if(tot==0){f[x]=0;return ;}//叶子节点直接返回
if(x==1)//根节点特判
{
if(tot==1)ans=max(ans,mxn);
else ans=max(ans,max(sec_mxn+1,mxn));
}
else if(tot>=2)ans=max(ans,mxn+1);//只有多个子树才需要转移记录答案
}
int main()
{
int t=read();
while(t--)
{
ans=0;
memset(f,127,sizeof(f));
memset(head,0,sizeof(head));
cnt=0;
n=read();
for(int i=1;i<n;i++)
{
int x=read(),y=read();
add(x,y);add(y,x);
}
dfs(1,0);
printf("%d\n",ans);
}
return 0;
}


