比基础更简单的进阶——线段树进阶
动态开点线段树
普通线段树一般来说需要 \(4n\) 的空间,但是动态开点线段树线段树只需要显式地记录每个节点的左右儿子节点编号。只需要开 \(2n\) 的空间。很显然,线段树一般来说共有 \(2n-1\) 个节点。
做到了空间上节约,其实我们也有复杂度常数上的节约(本人没有实际感受过,但是从理论上确实有效):因为对于程序运行来说,一颗树,或者是遍历时相邻的 \(2\) 个节点,下标相差不超过 \(2\) ,因为一个节点的 \(2\) 个儿子节点是在建树时紧跟该节点分别建立的。那么栈空间的调用就不需要重新启用空间,如果采用普通线段树也就是一个节点的左子节点为 \(2p\) ,右子节点为 \(2p+1\) 的方式,那么对于 \(p\) 较大的情况,很显然需要重新启用较远的空间,这样会增加一定的常数。
不过动态开点线段树一般是插入节点,不考虑初始直接建完整棵树的操作,所以很少在结构体中记录区间范围,而是考虑调用时直接下传操作。
代码实现:
void Ins(int &p,ll now,ll l,ll r)
{
if(!p)p=++tot;
if(l==r){/*Post Information*/return;}
ll mid=(l+r)>>1;
if(now<=mid)Ins(T[p].l,now,l,mid);
else Ins(T[p].r,now,mid+1,r);
UPDATE(p);
}
权值线段树
权值线段树本质是用线段树维护一个桶。
维护数列的权值线段树的每个节点对应一个数列上的数值,然后节点再存储这个数相关的信息。
不是很好理解?我们可以把它和普通的区间线段树做一个对比理解。
-
区间线段树:根节点存储整个区间,每个节点的子节点将父亲节点的区间分成 \(2\) 等分左右分别存储,叶子节点对应到每个单独的数的信息。
- 比如说存储区间和,那就对应每个节点对应 \([l,r]\) 存储这个区间的和,因为区间信息可并,所以父亲节点可以通过合并子节点得到。
-
权值线段树:根节点存储整个区间所有元素的总信息,每个节点的子节点将父亲节点对应的多个权值按分成 \(2\) 等分存储,叶子节点对应到每个单独的值的信息。
- 存储权值出现次数,那就对每个节点存储其对应权值 \(a_l\dots a_r\) 的信息,这个桶也是可并的(显然 \(1,2\) 的出现总次数等于其分别出现次数之和),所以父亲节点也可以合并子区间得到。而叶子节点显然对应各个权值本身的信息。
经典的数列第 \(k\) 大小问题可以用权值线段树解决。
代码实现:
int kth(int l,int r,int rt,int k)
{
if(l==r) return l;
else
{
int mid=(l+r)/2,s1=f[rt<<1],s2=f[rt<<1|1];
if(k<=s2)
return kth(mid+1,r,rt<<1|1,k);
else
return kth(l,mid,rt<<1,k-s2);
}
}
不过如果权值值域很大空间爆炸怎么办。
我们就可以采用离散化 \(+\) 之前提到的动态开点节约空间。
对于权值线段树记得记录根节点位置。
线段树合并
实现
线段树合并顾名思义,合并 \(2\) 棵线段树时进行的操作。
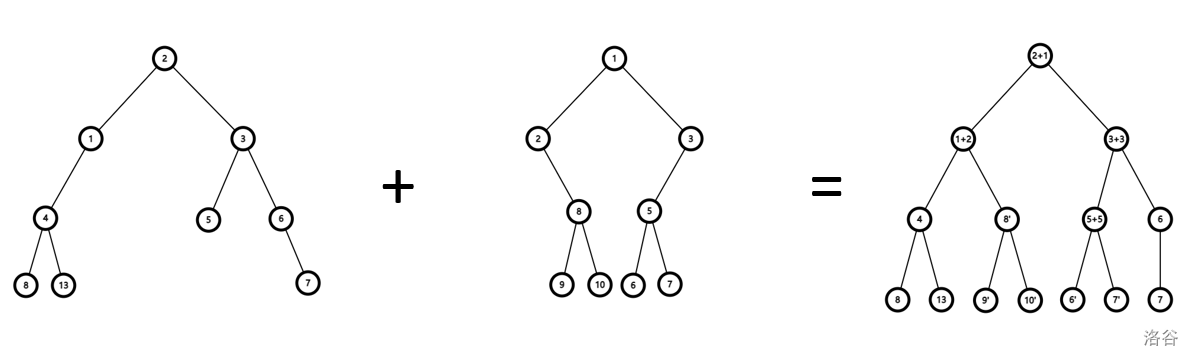
其实线段树合并就是在形态上取 \(2\) 棵线段树的并集。你可以理解为,取 \(2\) 张描摹纸画上这两棵线段树,然后把这两张纸重叠显现出来并起来的那棵树,就是合并的结果。
合并的操作在上图中也很显然地体现出来了:
设合并树的新节点 \(p\) ,合并的第一棵树节点 \(a\) ,第二棵为 \(b\)
- 对于 \(a,b\) 都有信息,则按题意合并 \(b\) 到 \(a\) 上,再赋值到 \(p\) 上;
- 对于 \(a\) 空 \(b\) 非空,直接对 \(p\) 赋 \(b\) 值;
- 对于 \(b\) 空 \(a\) 非空,直接对 \(p\) 赋 \(a\) 值;
- 递归处理左右子树;
- 回溯后更新当前节点;
- 返回 \(a\) 。
int Merge(int x,int y,int l,int r)
{
if(!x||!y)return !x?y:x;
if(l==r){/*Merge Information*/;return x;}
int mid=(l+r)>>1;
T[x].l=Merge(T[x].l,T[y].l,l,mid);
T[x].r=Merge(T[x].r,T[y].r,mid+1,r);
UPDATE(x);
return x;
}
复杂度
多棵 \(10^5\) 信息量级别的线段树合并,看起来并不会很快啊,那是怎么保证复杂度的呢?
我们来考虑如何证明复杂度。
其实要明白一个事,就是单次合并操作并没有严格保证的复杂度。
我们两棵树上 \(2\) 个相同位置的节点合并复杂度为 \(O(1)\) ,并且会少一个节点,那么我们就是 \(O(1)\) 花费减去一个节点。
我们有 \(n\) 个元素要插入多个树中,每个树的 \(\log n\) 层都会插入这么一个元素(也可以理解为动态开点的插入操作为 \(O(\log n)\) )。
现在考虑合并成一棵树,其实就是消去这 \(n\) 个元素分布在若干线段树中的不同位置直到对应的只剩一个,总体的最坏情况也就是分布于 \(n\) 个树各 \(\log n\) 层删除操作为 \(O(1)\) ,所以总体复杂度为 \(O(n\log n)\) 。
证毕。
线段树合并一般处理一些状态可并的区间问题,比如说从区间衍生到每一个子树的问题,可以考虑对子树开线段树再合并到父亲节点。
Luogu P3605 [USACO17JAN]Promotion Counting P
该问题只需要开权值线段树,用求 \(\texttt{kth-element}\) 类似的方法计算比当前节点大的子树上节点个数,然后考虑将子树合并到父亲节点即可。
代码实现:
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#define INL inline
using namespace std;
const int N=100005;
struct ReyE{int nxt,to;}e[N<<1];
struct Rey{int l,r,s;}T[N<<5];
int ans[N],cnt,tot,head[N],rts[N],a[N],b[N];
int nn,n;
INL void add(int u,int v)
{
e[++cnt].nxt=head[u];e[cnt].to=v;
head[u]=cnt;
}
INL int read()
{
int x=0,w=1;char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+ch-48,ch=getchar();
return x*w;
}
INL void UPDATE(int p)
{
T[p].s=T[T[p].l].s+T[T[p].r].s;
}
void Fix(int &p,int l,int r,int pos)
{
if(!p)p=++tot;
if(l==r){T[p].s++;return ;}
int mid=(l+r)>>1;
if(pos<=mid)Fix(T[p].l,l,mid,pos);
else Fix(T[p].r,mid+1,r,pos);
UPDATE(p);
}
int Vuq(int p,int l,int r,int L,int R)
{
if(!p)return 0;
if(l>=L&&r<=R)return T[p].s;
int mid=(l+r)>>1;
int res=0;
if(L<=mid)res+=Vuq(T[p].l,l,mid,L,R);
if(mid<R)res+=Vuq(T[p].r,mid+1,r,L,R);
return res;
}
int Merge(int x,int y,int l,int r)
{
if(!x||!y)return !x?y:x;
if(l==r){T[x].s+=T[y].s;return x;}
int mid=(l+r)>>1;
T[x].l=Merge(T[x].l,T[y].l,l,mid);
T[x].r=Merge(T[x].r,T[y].r,mid+1,r);
UPDATE(x);
return x;
}
void dfs(int x)
{
for(int i=head[x];i;i=e[i].nxt)
{
int go=e[i].to;
dfs(go);
rts[x]=Merge(rts[x],rts[go],1,nn);
}
ans[x]=Vuq(rts[x],1,nn,min(a[x]+1,nn),nn);
Fix(rts[x],1,nn,a[x]);
}
int main()
{
n=read();
for(int i=1;i<=n;i++)a[i]=b[i]=read();
sort(b+1,b+1+n);
nn=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;i++)
{
a[i]=lower_bound(b+1,b+1+nn,a[i])-b;
}
for(int i=2;i<=n;i++)
{
int x=read();
add(x,i);
}
dfs(1);for(int i=1;i<=n;i++){printf("%d\n",ans[i]);}
return 0;
}


