这不是NOIp 2020 T1!——网络流学习笔记

被迫营业（悲）

网络流的基本定义

网络流是一个大的图论算法集合，虽然只是一个图论算法，但是其功能可以应用到各种类型的问题中，所以十分重要。

网络

首先引用 \(\texttt{wiki}\) 定义

在图论中，网络流（英语：Network flow）是指在一个每条边都有容量（Capacity）的有向图分配流，使一条边的流量不会超过它的容量。通常在运筹学中，有向图称为网络。

简单来说，网络是个有向图 \(G=(V,E)\) ，这张图上的边权 \(c=(u,v),[(u,v)\in E]\) 并不代表其价值，实际上代表的是容量。\(u,v\)不联通时 \(c_{(u,v)}=0\)。

在一个网络中有源点 \(S\) 和汇点 \(T\) \([S,T\in V]\)。

所以我们考虑这样一个模型：在一个巨大的物流网络中，有一个一直出产的大工厂 \((S)\) 和集中收货的公司 \((T)\)。 但是很显然由于距离太远，快递们需要在不同的中转站 \((u_i) (v_i)\) 进行中转。但是每个中转站存储能力有限，所以并不能让所有商品同时存在一个中转站中，于是有了容量 \((\texttt{capacity}) (c_{(u,v)})\)一说 。

流

流 \((\texttt{flow})\) 定义为一个网络上的函数。这是一个定义在边上(也就是点的二元组)的实数函数，约定为 \(f(u,v)\space (u,v\in V)\)

对于一个流函数，\(f(u,v)\) 可以特称为一个边的流量，\(c(u,v)-f(u,v)\) 就是剩余流量 （还能做些什么？），而对于整个网络的流量我们定义为从源点 \(S\) 出发的流量之和:

\[\sum_{(S,v)\in E}f(S,v) \]

函数定义为

\[f(u,v)=\left\{\begin{aligned} &f(u,v)&(u,v)\in E\\ &-f(v,u)&(v,u)\in E \end{aligned}\right. \]

另外特有

\[f(u,v)=0[(u,v),(v,u)\notin E] \]

对于流还有以下约定

  • \(f(u,v) \leq c(u,v)\)
  • \(\forall x\in \complement_V\{S,T\} , f(u,x)=f(x,v)\) ，根据全局流量的定义，我们有： \(\sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)\)
  • 包括上面列出的 \(f(u,v)=-f(v,u)\)

这三点我们称之为 容量限制 流守恒性 斜对称性 。

我们继续考虑上面那个模型：现在你开始从工厂发货了，发货量巨大，很快快递们开始运输 \(( \texttt{flow} )(f(u,v))\) 每个中转站只有一定的存储量，所以有些货并不能及时运到下一个(容量限制)，显然，你将快递运回到上一个中转站，那属于负做功，所以有了(斜对称性)，快递员们很负责，他们一定会按质按量地送走一个中转站该送走的货物，其实也就是目前里面有的所有货物直至大公司(\(T\))，这是(流守恒性)。对于数据中心的统计，我们要考虑整个物流网络的工作效率，所以我们要算出运输流的综合，这就是整个网络的流量。

网络流模块主要是四种题目类型：最大流，最小割，费用流，上下界网络流

我们来分别探讨一下。

最大流

最大流问题是网络流问题的基础。

问题字面意思就是要求网络上从源点到汇点的最大流量。

\(\texttt{wikipeida}\) 上有一个较为全面的最大流算法表格，笔者在此引用并进行相关阐述。如有疏漏还望包容。

以下表格只是简述，部分算法会在下文详细分析。

\(\texttt{algorithm}\) \(\texttt{complexity}\) \(\texttt{About}\)
线性规划 / 字面意思，具体看这里
\(\texttt{Ford-Fulkerson}\) \(O(E\times f_{max})\) 贪心寻找增广路求最大流，复杂度和正确性其实并不稳定
\(\texttt{Edmonds-Karp}\) \(O(VE^2)\) 使用 BFS 求增广路的 \(\texttt{Ford-Fulkerson}\) 算法，保证在改进为每次总选择一条最短的增广路（路径长度单调增加），保证算法的正确性。
\(\texttt{Dinic}\) \(O(V^2E)\) 每次增广使用 BFS 重新给每个节点进行一个高度标记 \(H_i\) ，每次运用高度标记求阻塞流，直到发现汇点 \(T\) 的高度不存在即可停止增广。
\(\texttt{Dinic with Dynamic Trees}\) \(O(VE\log{V})\) 不会。也是 Dinic ，但是我不会动态树。
\(\texttt{Malhotra, Kumar, Maheshwari(MKM)}\) \(O(V^3)\) 仅限无环图。\(\texttt{Paper}\)
\(\texttt{Improved Shortest Augment Path(ISAP)}\) \(O(V^2E)\) 这名字有 SPFA 内味了。\(\texttt{ISAP}\) 理论上应该是 \(\texttt{Dinic}\) 的一个优化，因为每次求完增广路给每个点重新标记 \(H_i\) 在某些情况下貌似有写浪费，而标记的意义又在于分层，所以可以直接在 DFS 时就对每个没有出边可以增广的点重新标记。贪心求最小的不停增广直到有一个点经过两次就可以退出算法。
\(\texttt{KRT (King, Rao, Tarjan)}\) \(\displaystyle O(VE\log_{\frac{E}{V\log V}}V)\) 这个好厉害啊，笔者不会啊！惊恐
\(\texttt{Binary blocking flow algorithm}\) \(O(E\times \min\{V^{\frac{2}{3}},E^{\frac{1}{2}}\}\times\log{\frac{V^2}{E}}\times \log U)\) \(U\) 是复杂度常数，与 \(c_{max}\) 有关。这个也好牛逼啊！惊恐
\(\texttt{James B Orlin's + KRT (King, Rao, Tarjan)}\) \(O(VE)\) 分类讨论将算法复杂度维持在这个最优级别，卧槽好牛逼啊！惊恐惊恐惊恐
\(\texttt{Push-Relabel}\) \(O(V^2E)\) 笔者不是很会预流推送算法。但是也在此简述。首先在该算法中我们需要忽略流守恒性，我们允许流入的流量大于流出的流量，这个偏差 \(\delta(u)\) 我们称为超额流，然后再定义高度函数 \(h(i)\) 约束超额流只能从高点流向低点，当无法流出的时候再修改当前点的高度。\(u\) 超额，对于 \((u,v),[h(u)=h(v)+1]\)我们尽可能从 \(u\) 推送至 \(v\) ，如果 \((u,v)\) 推送完后满流，就删除。最后发现超额流全部流向 \(S\) ,网络重新满足流守恒性，最大流就是 \(\delta(T)\) 。
\(\texttt{HLPP}\) \(O(n^2\sqrt{m})\) 该算法就是优先推送高度高的溢出的结点以减少复杂度上界。每次选择溢出结点中高度最高的结点\(u\) ，并对它所有可以推送的边进行推送

接下来我们详细分析几个基础算法。

部分算法日后笔者熟练掌握后也会更新。

首先我们引入几个解决最大流必须清楚的定义。

残量网络

我们定义一条边的剩余流量为 \(c_f(u,v)=c(u,v)-f(u,v)\)

残量网络 \(G_f\) 则为所有 \(c_f(u,v)>0\) 的边重新构成的子图。

其实，有些边不一定存在于原图 \(G\) 中但是在残量网络 \(G_f\) 中，所以残量网络中可能包括反向边和一些特殊情况。

增广路

简单来说，残量网络上存在一条路径从 \(S\) 到 \(T\) 这条路径就可被称为残量网络。

增广路的作用就是不停更新不停求增广路直到不再存在增广便有最优解。

不过很显然不是直接求增广路的，我们需要利用网络的特性求增广路。

这样就要看各算法大显神通了。

Ford-Fulkerson

本质是找增广路的算法，考虑到复杂度和正确性存在的问题，我们直接来看优化后的 EK 算法。

Edmond-Karp ( EK 动能算法 )

这个算法就是在 \(\texttt{Ford-Fulkerson}\) 的基础上，采用 BFS 找增广路，每次重新对网络进行增广。

  • BFS 时，每一条路都要进行增广操作，重新减去当前流量。
  • 增广的时候选出最优的一条增广路，答案每次选取路径上最小流量。
  • 再重复 BFS 操作，直至不能再增广。

但是我们发现一些时候并不一定最优。

于是我们需要利用网络上反向边（也就是斜对称性）这样一个绝妙的建模

我们考虑这样一个情况：

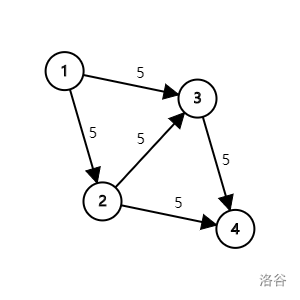
设这张图 \(S=1\) ，\(T=4\)。

如果在这张图上，我们直接走 \(1\rightarrow 2 \rightarrow 3 \rightarrow 4\)，我们发现不能再增广，这样\(flow_{max}=5\)，显然不正确。确实，这很显然，我们自己很容易发现，但是计算机不能。所以我们需要一个操作来辅助他们。

计算机有很强的运算能力，无论考虑多少情况他们都不累，所以我们只需要给他们一个类似悔棋的操作，他们会自己刨根问底。于是我们考虑具有斜对称性的反向边。

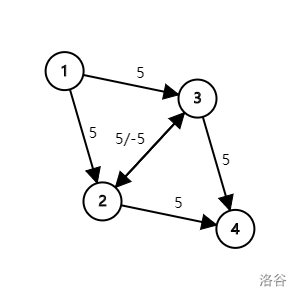
我们建立 \(3\rightarrow 2\) 的斜对称反向边，在 \(2\rightarrow 3\) 这一步我们就可以进行所谓反悔，我们发现，有了这个反悔操作，使得流向成为 \(1\rightarrow {\color{red}2\rightarrow 3\rightarrow 2} \rightarrow 4\)，我们相当于直接抵消了\((3,2)\) 这条边，这样流量分为 \(1\rightarrow 3\rightarrow 4,1\rightarrow 2\rightarrow 4\)，就得到了 \(flow_{max}=10\)

电脑很快，他会很快地跑遍所有的情况，包括反向边，所以自然而然你会得到最优的增广。

这个证明很简单，就是说，如果对于 \((x,y)\)，\(f(x,y)>0\)，则必然有 \(f(y,x)<0\) ，则 \(f(y,x)<c(u,x)\) 所以算法必然会遍历这些反向边。

具体代码实现在细节上有一些注意点：

  • 建图我们初始值设 cnt=1; 这样第一个点编号为 \(2\) ，在建反向边的时候编号为 \(3\) ，所以我们得到正向偶反向奇的特性。这样在统计时 u 代表当前边那么 u xor 1 就代表反向边。（当然，如果是邻接矩阵那就直接用 e[x][y] 和 e[y][x] 。
  • BFS 的过程中，我们每次直接选取相距最近的边赋流，不需要担心，反正都会跑一遍。
  • 如果汇点没有收到任何流量，则结束，说明没有增广路，如果有，那不要忘记更新残量网络 \(G_f\)。
  • 答案每次显然是加上增广路上最小流量。因为那才是可行流。

代码大家可以百度参考一下，笔者 EK 写的比较丑。

Dinic

这个貌似是最受欢迎的网络流算法之一了吧？因为好写。但是其实他常数算比较大的了。但是有一说一一般出题人很少卡，所以是初学者首选之一。

首先如表格中所说，\(\texttt{Dinic}\) 算法需要给节点标记高度 \(H_i\) 。 首先定义 \(H_S=0\) 那么定义每条边的距离为 \(1\) ，那么一个点到源点的最短距离就为其高度 \(H\)。

\(\texttt{Dinic}\) 的优秀之处在于如下几点：

  • 分层后保证 可以及时退出程序 而不是跑完再判断是否退出，因为一旦汇点的层数没有标记，说明不连通，那就没有必要再跑。
  • 分层后依然保证每次可以取到最短的增广路，因为每次我们只对 \(H_v=H_u+1\) 的 \((u,v)\) 增广。
  • 多路程增广：由于是 DFS 找增广路，所以支持多线程求路径，如果流量还有剩余，就一并解决，再增广。也就是说，现在流水可以开始扭头分岔了，开分身打架。
  • 当前弧优化：一条路只会被增广一次，就像最短路的 vis[] 数组一样，我们可以考虑每次增广不去走上一次走过的边。如此一来，配合多线程增广，我们很快可以增广所有的情况。

具体可以看一下代码：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<stack>
//#include<bits/stdc++.h>

#define INF (1ll<<60)
#define ll long long
#define ull unsigned long long
#define INL inline
//Tosaka Rin Suki~
using namespace std;

INL void read(int &x)
{
	 x=0;int w=1;
	 char ch=getchar();
	 while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
	 if(ch=='-')w=-1,ch=getchar();
	 while(ch>='0'&&ch<='9')
	 {x=(x<<1)+(x<<3)+ch-48,ch=getchar();}
	 x*=w;
}

INL int mx(int a,int b){return a>b?a:b;}
INL int mn(int a,int b){return a<b?a:b;}

struct Rey
{
    int nxt,to;
    ll val;
}e[5000005];
int n,m,s,t;
int cnt=1,head[200005],now[200005];
ll dis[200005];

void add(int u,int v,ll w)
{
    e[++cnt].nxt=head[u];
    e[cnt].to=v;
    e[cnt].val=w;
    head[u]=cnt;
}

bool bfs()//bfs 分层
{
    for(int i=1;i<=n;i++)
    {
        dis[i]=INF;
        if(i==s)dis[i]=0;
    }
    queue <int> q;
    q.push(s);
    now[s]=head[s];
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(e[i].val>0&&dis[v]==INF)
            {
                q.push(v);
                now[v]=head[v];
                dis[v]=dis[u]+1;//分层
                if(v==t){return 1;}
            }
        }
    }
    return 0;//未到达过 T
}

ll dfs(int x,ll s)//dfs 求增广路
{
    if(x==t)return s;
    ll res=0;
    ll C;
    for(int i=now[x];i&&s;i=e[i].nxt)
    {
        now[x]=i;//当前弧优化
        int v=e[i].to;
        if(e[i].val>0&&dis[v]==dis[x]+1)
        {
            C=dfs(v,min(s,e[i].val));
            if(!C)
            {
                dis[v]=INF;
            }
            e[i].val-=C,e[i^1].val+=C;//重新统计
            res+=C;
            s-=C;
        }
    }
    return res;
}

ll ans;

int main()
{
	//freopen("P3376.in","r",stdin);
	//freopen("P3376.out","w",stdout);
    read(n);read(m);read(s);read(t);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        ll w;
        read(u);read(v);scanf("%lld",&w);
        add(u,v,w);add(v,u,0);
    }
    while(bfs())
    {
        ans+=dfs(s,INF);
    }
    printf("%lld\n",ans);
	return 0;
}

\(\texttt{Dinic}\) 的时间复杂度需要注意。虽然是 \(O(V^2E)\) 的（每次增广后 \(H_i\) 不会减小，甚至 \(H_T\) 必然增大，所以增广最多为 \(V-1\) 次，而一次增广在优化后，一条当前弧最多变化 \(E\) 次，所以是 \(O(V^2E)\) 的），但是一般来说跑不满，而且在二分图匹配问题中，只有 \(O(E\sqrt{V})\) ，\(\texttt{OI-wiki}\) 上给出的证明非常详细，可以参考一下。

Improved Shortest Augment Path(ISAP)

如在上表格中所说，\(\texttt{ISAP}\) 是 \(\texttt{Dinic}\) 进一步的优化和提升。复杂度很是优秀。在这里只给出写法。

\(\texttt{ISAP}\) 同样是打高度标记，但是是从 \(T\rightarrow S\) 进行 BFS ，这样反过来就是我们只找比当前点层数少 \(1\) 的点进行增广。

优化之处在于，我们不需要重新打标记，而是在增广时顺带重新分层。增广完点 \(u\) 后，我们遍历所有出边找到最小的 \(H_v\) 然后令 \(H_u=H_v+1\) 。没有出边则 \(H_u=V\)。

当 \(H_S\geq V\) 便停止算法。

\(\texttt{ISAP}\) 除了当前弧优化，还存在一个叫做 \(\texttt{GAP}\) （断层优化）的东西，我们记录每一层有的点的数量，一旦发现某一层没有点了，那么出现断层，也就不存在增广路了，就可以直接停止算法。

Push-Relabel 预流推进算法 & HLPP

不会，咕咕咕。

最小割

最小割是个很ez的定理。

首先给出概念定义。

割

对于网络流图 \(G=(V,E)\) ，我们将点集 \(V\) 进行划分为 \(2\) 个集合 \(S_1\) 和 \(S_2\) 。令 \(S\in S_1,T\in S_2\) 。

定义割 \((S_1,S_2)\) 的容量 \(c(S_1,S_2)=\displaystyle\sum_{u\in S_1,v\in S_2}c(u,v)\) 。

定义一个最小割就是 \(c(S_1,S_2)\) 最小的割。

最大流最小割定理

有定理：\(f(S_1,S_2)_{\max}=c(S_1,S_2)_{\min}\)

证明：

约定集合定义下的 \(f(X,Y)=\displaystyle \sum_{u\in X,v\in Y}f(u,v)-\displaystyle \sum_{u\in X,v\in Y}f(v,u)\leq \sum_{u\in X,v\in Y}f(u,v)\leq \sum_{u\in X,v\in Y} c(u,v)=c(X,Y)\)

我们这里证明并不适用斜对称性，因为斜对称性是在残量网络上求解最短路辅助用的特性，这里的和值为 \(u\) 出发 和 \(v\) 出发的流量和。其实符合的是流量平衡，需要转换一下。

那么对于最大流：

我们考虑当前图上最大流 \(f_{\max}\) ，因为是最大流，很显然不存在增广路，则必然对于任意点对 \((u,v)\) 且 \((u\in S_1, v\in S_2)\) ，\(f(u,v)\) 必然满流所以 \(f(u,v)=c(u,v)\) 。既然满流，那么反向的入边则必然没有流量可走所以 \(f(v,u)=0\)

所以发现：

\(f(S_1,S_2)_{\max}=\displaystyle \sum_{u\in X,v\in Y}f(u,v)-\displaystyle \sum_{u\in X,v\in Y}f(v,u)=\displaystyle \sum_{u\in X,v\in Y}c(u,v)-\displaystyle 0=c(S_1,S_2)_{\min}\)

所以得到定理。

既然知道这个定理，最小割问题就迎刃而解了。

我们可以来看几个建模。

这是一道最小割的模板题，但是初学看到题目还是想不出来为什么是最小割。

这就是网络流的巧妙之处，我们考虑建立模型。

\(2\) 个条件：

  • 为了朋友立场违背自身意愿
  • 违背朋友意愿

首先考虑割的 \(2\) 个点集为 \(A\) 与 \(B\) 显然分别代表 \(2\) 种观点。每个小朋友各自的观点分别连向应该在的点集

显然会出现这种两个独立的情况。

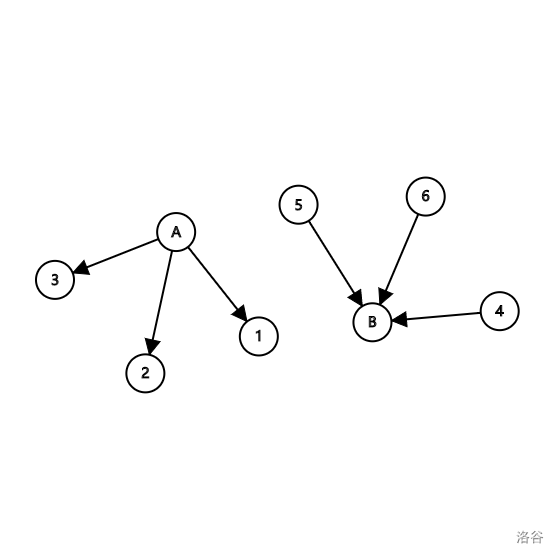
我们现在引入条件 \(2\) ，与好朋友的矛盾冲突。

显然，如果没有条件 \(2\) ，脑子正常的小朋友就不会违背自身意愿，我们可以理解为条件 \(2\) 牵动着条件 \(1\)。

冲突的定义在这题分别为条件 \(1\) \(2\)，也就是说 朋友意见不和 那就是必然冲突。

如果我们定义源点汇点为立场本身，那么直接连向源点汇点的边表示 自身意愿。

我们转化一下 我们与汇源点的连边代表 —— 我们自己对自己要求的立场

我们代入情境，发现如果与矛盾边连边，那么就是 他人对我们要求的立场 或者 我们对他人要求的立场，考虑模型，如果是朋友却有矛盾，我们会出现一条双向边。

这里考虑反证法：如果是单向边，那么不符合对称性，如果不符合对称性，图本身并不存在 \((A,B)\) 通路，不会有冲突。

于是也许会变成如下建图。

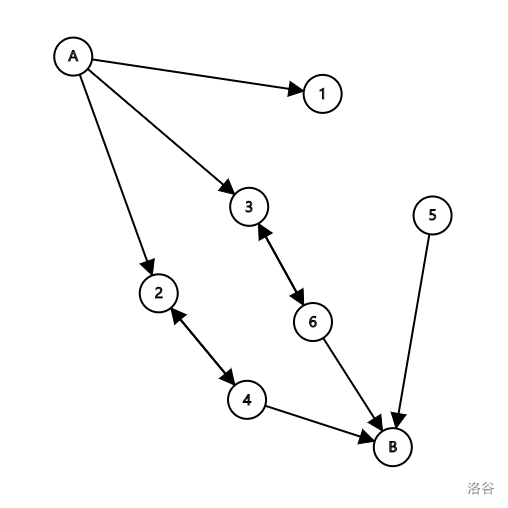
那么如何对最小冲突求解呢

解决条件 \(1\) 我们直接割边改变自己立场

解决条件 \(2\) 我们改变二者中一人矛盾的立场所以也是割边

那么最小冲突，就是 最小割。

代码如下：

#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstdio>
#include<queue>

using namespace std;

int n,m,s=0,t;

struct Rey
{
	int nxt,to,val;
}e[1000000];

int head[3005],cnt=1;
int H[3005],cur[3005];

const int inf=1<<30; 

void add(int u,int v,int w)
{
	e[++cnt].nxt=head[u];
	head[u]=cnt;
	e[cnt].to=v;
	e[cnt].val=w;
}

queue <int> q;

bool bfs()
{
	memset(H, -1 ,sizeof(H));
	H[s]=0;
	q.push(s);
	cur[s]=head[s];
	while(!q.empty())
	{
		int now = q.front();q.pop();
		for(int i=head[now];i;i=e[i].nxt)
		{
			int go=e[i].to;
			if(H[go]==-1 && e[i].val>0)
			{
				H[go] = H[now]+1;
				cur[go] = head[go];
				q.push(go);
			}
		}
	}
	if(H[t] == -1)return 0;
	else return 1;
}

int dfs(int x,int s)
{
	if(x == t)return s;
	int flow=0,c=0;
	for(int i = cur[x]; i&&s ; i=e[i].nxt)
	{
		cur[x]=i;
		int go = e[i].to;
		if(e[i].val>0&& H[go] == H[x]+1)
		{
			c=dfs(go,min(s,e[i].val));
			if(!c){H[go]=inf;continue;}
			e[i].val-=c;
			e[i^1].val+=c;
			flow+=c;
			s-=c;
		}
	}
	return flow;
}

int ans;

void Dinic()
{
	while(bfs())
	{
		ans+=dfs(s,inf);
	}
	return ;
}

int main()
{
	scanf("%d %d",&n,&m);
	t=n+1;
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		if(x){add(s,i,1);add(i,s,0);}
		else {add(i,t,1);add(t,i,0);}
	}
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		add(x,y,1);add(y,x,0);add(y,x,1);add(x,y,0);
	}
	Dinic(); 
	printf("%d\n",ans);
	return 0;
}

这又是一个二者择其一的模型。

与上面一题类似，我们考虑将 \(2\) 块田地分为 \(2\) 个集合。

对于独立的作物，我们分别向源汇点连边表示贡献值。

考虑操作 割 ，毕竟二者择其一，那么显然割掉各店与 \(A\) ， \(B\) 分别的连边表示不这么种。

那么我们只需要考虑 作物集合 带来的额外收益如何考虑。

首先显然最优解就是 总收益减去最小割。

首先我们观察根据每个点建立的模型：

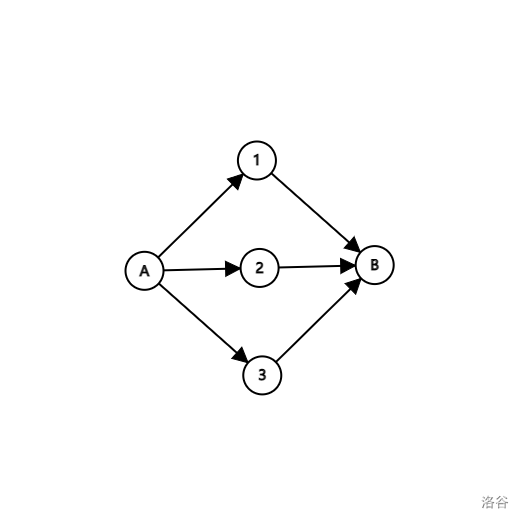
对于一个点集 \(\{u,v,w\}\) 只要任意一点不种在一起，该集合的额外收益都无效。

如果要求最小割，那么我们必须在割完后不能再让图从 \(A\rightarrow B\) 连通。

所以对于一个点集，割任何一个不同的方向的边都会导致收益消失，如果都是同一方向那也会让另一方向的收益消失。我们不能对各连再连边。

为了体现点集的特性，我们抽象地开一个虚点将一个集合表示为一个点。所以会出现如下情况：

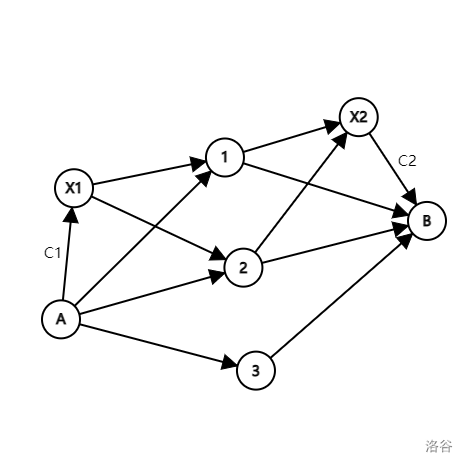
显然如果任何一个点不一，\(C1,C2\) 都会被割断，因为要变成不连通的情况。如果方向都一样，那么也要割断另一边的那一条，这样也会不联通，但是点与点集之间是不能割边的，因为这样也会不联通，但是这不是合法操作，所以我们可以设置虚点与点之间的边为 $+\infty $

这样建模就结束了。

代码如下：

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>

using namespace std;

const int INF=2147483646; 

int n,m;
int head[1000005];
struct Rey
{
	int nxt,to,val;
}e[5000005];
int sum,cnt=1;
int s,t;

queue<int> q;

int k,c1,c2;

int H[1000005],cur[1000005];

inline void add(int u,int v,int w)
{
	e[++cnt].nxt=head[u],e[cnt].to=v,e[cnt].val=w,head[u]=cnt;
	e[++cnt].nxt=head[v],e[cnt].to=u,e[cnt].val=0,head[v]=cnt;
}

inline bool bfs()
{
	while(!q.empty())q.pop();
	memset(H,-1,sizeof(H));
	H[s]=0;
	q.push(s);
	cur[s]=head[s];
	while(!q.empty())
	{
		int now=q.front();
		q.pop();
		for(int i=head[now];i;i=e[i].nxt)
		{
			int go=e[i].to;
			if(e[i].val>0&&H[go]==-1)
			{
				H[go]=H[now]+1;
				q.push(go);
				cur[go]=head[go];
				if(go==t)return 1;
			}
		}
	}
	if(H[t]==-1)return 0;
	else return 1;
}

inline int dfs(int x,int s)
{
	if(x==t)return s;
	int res=0,c=0;
	for(int i=cur[x];i&&s;i=e[i].nxt)
	{
		cur[x]=i;
		int go=e[i].to;
		if(e[i].val>0&&H[go]==H[x]+1)
		{
			c=dfs(go,min(s,e[i].val));
			if(!c){H[go]=-1;continue;}
			e[i].val-=c;
			e[i^1].val+=c;
			res+=c,s-=c;
		}
	}
	return res;
}

int main()
{
	scanf("%d",&n);s=n+1;t=n+2;
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		add(s,i,x);sum+=x;
	}
	for(int i=1;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		add(i,t,x);sum+=x;
	}
	scanf("%d",&m);
	for(int i=1;i<=m;i++)
	{
		scanf("%d %d %d",&k,&c1,&c2);sum+=c1+c2;
		add(s,i+t,c1);add(i+t+m,t,c2); 
		while(k--)
		{
			int x;scanf("%d",&x);add(i+t,x,INF);add(x,i+t+m,INF); 
		}
	}
	int dec=0;
	while(bfs()){dec+=dfs(s,INF);}
	printf("%d\n",sum-dec);
	return 0;
}

费用流

我们给网络 \(G=(V,E)\) 每条边的容量 \(c(u,v)\) 的基础上再加上对于单位流量的费用 \(w(u,v)\)

也就是说，当 \((u,v)\) 的流量为 \(f(u,v)\) 时需要花费 \(f(u,v)\times w(u,v)\) 的费用。

一般来说，\(w(u,v)=-w(v,u)\)

费用流问题一般就是让我们求：

在 \(\displaystyle \max\sum_{(u,v)\in E}f(u,v)\) 的前提下保证 \(\displaystyle \min \sum_{(u,v)\in E} f(u,v)\times w(u,v)\)

SSP (Successive Shortest Path)

这是一个贪心算法，本质只是将最大流求增广路的过程改为 每次求单位费用最小的增广路进行增广 ，直到不存在增广路。

因为涉及到最短路相关的问题，所以这个算法对于负环非常敏感，我们后面会提到一些科技来解决负环问题。

关于这个贪心的正确性，\(\texttt{OI-wiki}\) 仍然给出了详细的证明。

我们只略提一下：假设算法求出的前 \(i-1\) 条的最小费用为 \(f_{i-1}\) ，那么对于该算法再求出一条最短增广路得到 \(\min\{f_{i}\}\) ,如果该 \(f_i\) 不是最优，那么显然对于如果存在的更优的 \(f_i'\) ，\(f_i'-f_{i-1}\) 不会是最短增广路， 那只能出现负环，而对于负环：一是不能出现，二是即使存在负环，那 \(f_{i-1}\) 也不可能为前 \(i-1\) 的最小费用，因为我们只需要多往这个负圈流，费用就会更小。 所以贪心正确。

这个算法实现非常简单，你只需要将 \(\texttt{EK}\) 和 \(\texttt{Dinic}\) 算法中的求增广路的过程加上一个 \(\texttt{SPFA}\) ,（因为负环所以不适用 \(\texttt{Dijkstra}\) ）。

代码：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<stack>
//#include<bits/stdc++.h>

#define ll long long
#define ull unsigned long long
#define INL inline
//Tosaka Rin Suki~
using namespace std;

const int N=5005;
const int M=50005;

INL void read(int &x)
{
	 x=0;int w=1;
	 char ch=getchar();
	 while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
	 if(ch=='-')w=-1,ch=getchar();
	 while(ch>='0'&&ch<='9')
	 {x=(x<<1)+(x<<3)+ch-48,ch=getchar();}
	 x*=w;
}

INL int mx(int a,int b){return a>b?a:b;}
INL int mn(int a,int b){return a<b?a:b;}

struct Rey
{
	int nxt,to;
	ll val,c;
}e[M<<2];
int cnt=-1,head[N];
ll nowmn[N],pre[N];
ll dis[N];
bool vis[N];

void add(int u,int v,ll w,ll c)
{
	e[++cnt].to=v;e[cnt].nxt=head[u];
	e[cnt].val=c;e[cnt].c=w;
	head[u]=cnt;
}

int n,m,s,t;

bool SPFA()
{
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	queue <int> q;
	q.push(s);
	dis[s]=0;vis[s]=1;nowmn[s]=1ll<<60;
	while(!q.empty())
	{
		int now=q.front();q.pop();
		vis[now]=0;
		for(int i=head[now];~i;i=e[i].nxt)
		{
			if(e[i].c<=0)continue;
			int go=e[i].to;
			if(dis[go]>dis[now]+e[i].val)
			{
				dis[go]=dis[now]+e[i].val;
				nowmn[go]=min(nowmn[now],e[i].c);
				pre[go]=i;
				if(!vis[go])
				{
					q.push(go);	vis[go]=1;
				}
			}
		}
	}
	if(dis[t]==4557430888798830399)
	{
		return 0;
	}
	else return 1;
}

ll ans1,ans2;

void SSP()
{
	while(SPFA())//改为 SPFA
	{
		int to=t;
		ans1+=nowmn[t];
		ans2+=1ll*dis[t]*nowmn[t];
		int now=0;
		while(to!=s)
		{
			now=pre[to];
			e[now].c-=nowmn[t],e[now^1].c+=nowmn[t];
			to=e[now^1].to;
		}
	}
}

int main()
{
	//freopen(".in","r",stdin);
	//freopen(".out","w",stdout);
	read(n);read(m);read(s);read(t);
	memset(head,-1,sizeof(head));
	for(int i=1;i<=m;i++)
	{
		int u,v;
		ll w,c;
		read(u);read(v);
		scanf("%lld %lld",&w,&c);
		add(u,v,w,c);
		add(v,u,0,-c);
	}
	SSP();
	printf("%lld %lld\n",ans1,ans2);
	return 0;
}

Primal-Dual 原始对偶算法

如果您是 "关于 SPFA 它已经死了" 说法的信徒，那么可以去学习这个算法，博主比较菜，不会。

推荐阅读

不过这个还不是消圈算法，我们来看一下消圈算法。

费用流消圈

如果一个网络流中求出的最小费用最大流中存在一条增广路有负权路径，那么这条最大流不合法，因为在这个残量网络上我们可以改流至这条负权路减少费用。不过反过来思考，我们可以转而利用这个思路。

我们只需要将流尽可能地分到这些负权路径，直到不可再分，发现负环不再存在。

笔者不是很熟练这个算法。因为貌似还有一种黑科技可以解决负环问题，我们在下文会提到。

上下界网络流

上下界网络流是一般网络流建模题的最重要一步。

一般来说，按字面意思来看，本质就是为流量设置上界以外还要求了下界。

设容量限制 \(c(u,v)\) 与流量下界 \(b(u,v)\) ，要求边流量 \(b(u,v)\leq f(u,v)\leq c(u,v)\) 。

同时满足继续网络流基本性质。

无源汇上下界可行流

不给定源汇点，询问对于有上下界的网络，是否存在方案使得每条边符合流量平衡并满足上下界。

我们首先考虑上界，对于每条边我们设置初始流量 \(f_0(u,v)=b(u,v)\)

显然，初始情况很有可能是不符合流量平衡的，所以我们设对于点 \(u\) 初始的 流入流量减去流出流量为 \(\delta(u)\)

  • \(\delta(u)=0\) 流量平衡
  • \(\delta(u)>0\) 入流 \(>\) 出流，我们添加流向 \(u\) 的边，流量为 \(|\delta(u)|\)
  • \(\delta(u)<0\) 出流 \(<\) 入流，我们添加流出 \(u\) 的边，流量为 \(|\delta(u)|\)

我们发现，如果给原网络并上这些附加边的流，就是一个可行方案，所以我们跑最大流，如果这些边满流，则存在方案。

对于上界的判定，我们在初始条件时先建好 \((u,v)'\) 使得流量为 \(b(u,v)-c(u,v)\) 防止溢出。

有源汇上下界可行流

考虑 \((S,T)\) 的上界为 \(+\infty\) 下界为 \(0\)

转换成无源汇上下界可行流。

有源汇上下界最大流

我们先做可行流。

然后删去合并的边求残量网络，然后再 在残量网络上 跑 \((S,T)\) 的最大流。

然后记得答案是可行流流量和残量网络上的最大流流量的和。

有源汇上下界最小流

同理，先退流，然后求残量网络。

然后跑 \((T,S)\) 的最大流，可行流减去最大流就是答案。

上下界网络流消圈

这就是我们提到的黑科技。

参考 Luogu P7173 【模板】有负圈的费用流

我们考虑一个等效的情况：对于一个边如果满流 \(c\) ，退流 \(c-f\) 就相当于流了 \(f\)。

对于负权边 \((u,v)\) \(w<0\)

我们可以先满流，然后退流，退流的时候权值为 \(-w\)，这样程序执行的流量就为正权了。

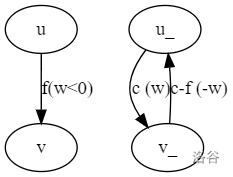
操作可以用上下界网络流解决。

小结

其实上下界网络流就已经不再设计算法内容了，更多的是建模思路。

对于网络流模型的建立实在太多太多，最经典的莫过于网络流24题。

对于建模的思考，我们可以参考 2016国家集训队论文 《网络流的一些建模方法》——姜志豪 东营市胜利第一中学

就这样先完结吧，其实还有很多要学的。

\[\text{网络流部分}\texttt{——2021.01.25~28} \text{写在笔记本电脑前} \]

Reference：

posted @ 2021-01-25 16:24  Reywmp  阅读(438)  评论(0)    收藏  举报