禁止近距离接触——差分约束

模拟赛遇到不会的东西，随便写点。

差分约束模型一般建立在\(m\)个\(n\)元一次不等式上。对于这个矩阵应当满足系数矩阵每一行有且仅有一个\(-1\) 和 \(1\)。

\(\texttt{e.g.}\)

\[\left[ \begin{array}{ccc} 0 & 1 & -1 & 0\\ -1 & 0 & 1 & 0\\ 0 & 1 & 0 & -1\\ 0 & 0 & 1 & -1\\ \end{array} \right] \left( \begin{array}{ccc} x_1\\ x_2\\ x_3\\ x_4\\ \end{array} \right) \leq \left( \begin{array}{ccc} 1\\ 8\\ 4\\ 7\\ \end{array} \right) \]

我们可以借此联想到三角不等式。

\[\begin{cases} x_b-x_a\leq A\\ x_c-x_b\leq B\\ x_c-x_a\leq C\\ \end{cases} \rightarrow x_c-x_a\leq A+B \]

\[\therefore \text{max} \left\{ x_c-x_a \right\}=\text{min} \left\{ A+B,C \right\} \]

很显然，我们更容易想到建立在三角不等式上的这个模型：

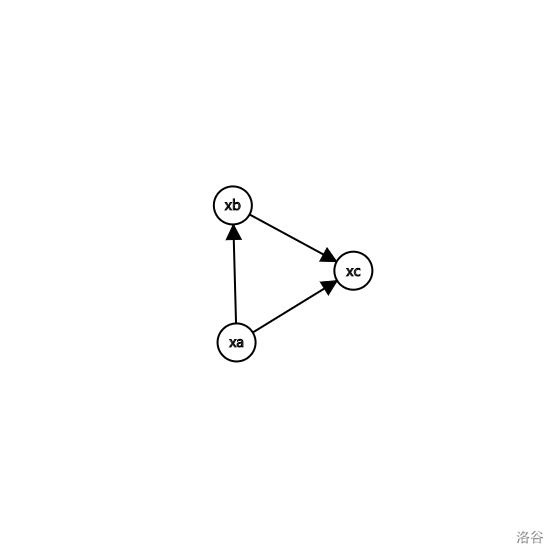
这就是最短路松弛的经典模型。

if(d[u]+e(u,v)<d[v]){d[v]=d[u]+e(u,v);}

构建模型的过程也很简单：

对于 \(x_a-x_b \leq c\) 得出 $ b \rightarrow a$ 可以连一条 $ c $ 的边。add(b,a,c)

显然，\(x_a-x_b \geq c\) 转换为 \(x_b - x_a \leq -c\) 就与上同理了。

我们将不等式组推广成\(n\)元，\(m\)个，整个模型自然就成为了\(s \rightarrow t\)的最短路计算。

• 解的存在性

如果连通图存在负环，那么 \(x_s,x_t\) 间的路径会被无限松弛，dis[t]-dis[t]=-inf。抽象出来就是 \(d_t-d_s \leq -\infty\)，所以 \(\max \left\{ d_t-d_s \right\}\) 不存在。便是无解。

如果本身图不连通，也就是不存在$ s \rightarrow t$的路径，那么 \(s\) 与 \(t\) 显然没有约束条件，也就有无限个解。

• \(\texttt{Tricks and Tips}\)

• 对于有负环的图显然我们选择\(\texttt{Bellman - Ford}\)解决问题。

• 线性模型的差分约束就是普通的差分约束模型，直接在限制关系两点间建边。

• 区间模型的差分约束与线性大同小异，直接对区间头尾进行最短路。

• 未知约束条件

如果说 \(x_a-x_b \leq K\) 这个 \(K\) 为常量，在 \(K\) 不确定的情况下，我们直接采用暴力枚举的方法找 \(K\) ，由于不等式给出，所以状态很好定义，我们就可以进一步优化为二分答案的方法。

例题 \(\texttt{HDU P1529}\)

---

Reference：

• 夜深人静写算法（四） - 差分约束