后 浪——平衡树( Splay )初步学习笔记
占坑写笔记,不忘初心,牢记使命(雾)
简介
\(\text{Splay}\)是一种可以用来高效率维护二叉查找树的平衡树,又称伸展树,分裂树,\(1985\)年由\(\text{Daniel Sleator}\)和\(\text{Robert Endre Tarjan}\)(又是他orz)提出发明的高级(大概)数据结构。
关于BST
学习\(\text{Splay}\)前,显然你应该先了解\(\text{Binary Search Tree}\)这一种基本数据结构,这里不多做介绍。
但是为了保证阅读体验良好,我们在这里介绍部分\(\text{Binary Search Tree}x\)的相关性质。
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- \(\text{BST}\)的 删除、查找、插入 等操作的复杂度显然为其建成的树型结构的层数,一般期望为\(O(\text{log} n)\);
- 显然\(\text{BST}\)的中序遍历就是一个有序序列。
但是,一旦遇到一些毒瘤数据,简单的\(\text{BST}\)结构很容易被卡掉,会由树退化成一个线性表,复杂度直线上升到\(O(n)\),更珂怕的是,这种情况并不少见,非常容易卡掉\(\text{BST}\)
\(\texttt{e.g}\) 给定有序序列 \(1,5,7,8,9,10,11,15\)
如果我们插入时默认\(1\)作为\(\texttt{root}\)且不做改变,那么会出现一种尴尬的情况:
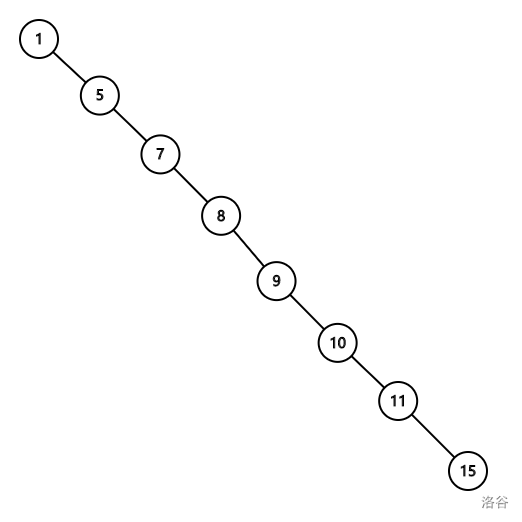
所以我们很显然需要通过改变根节点和子树位置来维护这棵树,保证其复杂度均摊成\(O(\text{log} n)\)
于是平衡树应运而生。
对于这个例子,我们只需要简单的改变一下构造方法:
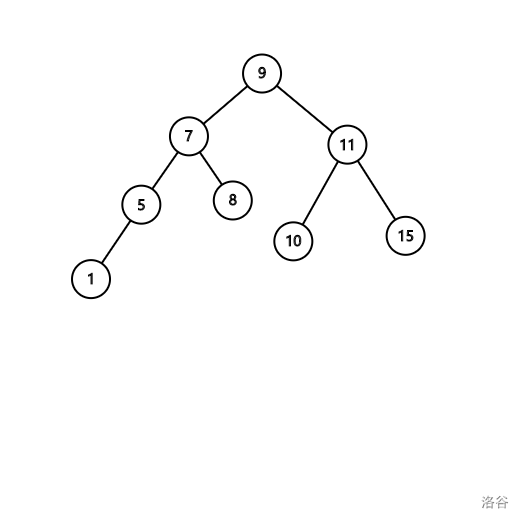
就可以使这个复杂度大大降低,我们称这种操作为旋转。\(\text{Splay}\)就是在这种操作的基础上进一步维护整棵树
为什么是Splay
平衡树是一个大佬云集的模块,各种高级平衡树实现算法层出不穷,如红黑树,\(\text{Treap}\),\(\texttt{FHQ-}\text{Treap}\),\(\texttt{AVL}\)树,\(\text{B}\)树,\(\texttt{WBLT}\)等一系列平衡树实现方法。
在\(\texttt{OI}\)学习中,\(\text{Splay}\)可谓是使用范围广泛,功能强大并且效率高这般的十分优秀。
\(\text{Splay}\)的优秀之处主要在于 极高的效率 和 强大的功能
- \(\text{Splay}\)会将被经常查询的节点移向根节点的方向,来保证均摊高效的复杂度。
- \(\text{Splay}\)不仅时间效率优秀,空间效率也优秀,因为\(\text{Splay}\)并不需要像\(\text{Treap}\)那般维护一个堆性质,也不需要存储额外信息,因为其巧妙的算法设计,\(\text{Splay}\)唯一需要注意的就只是自身的伸展与分裂。
- \(\text{Splay}\)的分裂与伸展使其在区间操作时体现强大的功能,详见Luogu P3391 【模板】文艺平衡树和Luogu P2042 [NOI2005]维护数列。
Splay
节点信息
全局:
| 变量名 | 记录信息 |
|---|---|
root |
根节点 |
cnt |
总节点数 |
树上:
| 变量名 | 记录信息 |
|---|---|
val |
权值 |
fa |
父亲节点 |
ch[0/1] |
左/右子节点 |
siz |
子树大小 |
tot |
节点权值在序列中出现次数(一般来说保证没有权值相同的节点) |
大部分情况下,我们可以用class或者struct方便地记录这些信息,更有较为复杂的指针实现方式,但是我不会写。
- 各类操作:
维护siz
这个比较简单,类似于线段树的节点信息更新。
显然当前节点的siz就是左右子树大小和自身大小的和
void UPDATE_size(int p){T[p].siz=T[T[p].ch[0]].siz+T[T[p].ch[1]].siz+T[p].tot;}
查询方向
用来查找当前节点与其父亲节点的相对方位
int POS_ch(int p){return p==T[T[p].fa].ch[1]?1:0;}
整块销毁
这个不是删除序列中的一个元素,而是直接暴力销毁整个节点,貌似并不会用到,OI-wiki写了我还是加上吧
void DEL_all(int p){T[p].ch[0]=T[p].ch[1]=T[p].fa=T[p].siz=T[p].val=T[p].tot=0;}
旋转
这个是重中之重的操作,我们详细地来讲解一下。
对于\(\text{Splay}\)我们之前说过:
\(\text{Splay}\)会将被经常查询的节点移向根节点的方向,来保证均摊高效的复杂度。
那么一个节点被旋转以后,我们就将\(\texttt{root}\)直接指向旋转后的根节点,这样便是伸展。
并且,我们归根结底还是要将整棵平衡树维护成一个\(\text{BST}\),所以说,其中序遍历不可以改变。
我们有2种旋转方式,相互对应。
左旋和右旋
我们看图理解一下
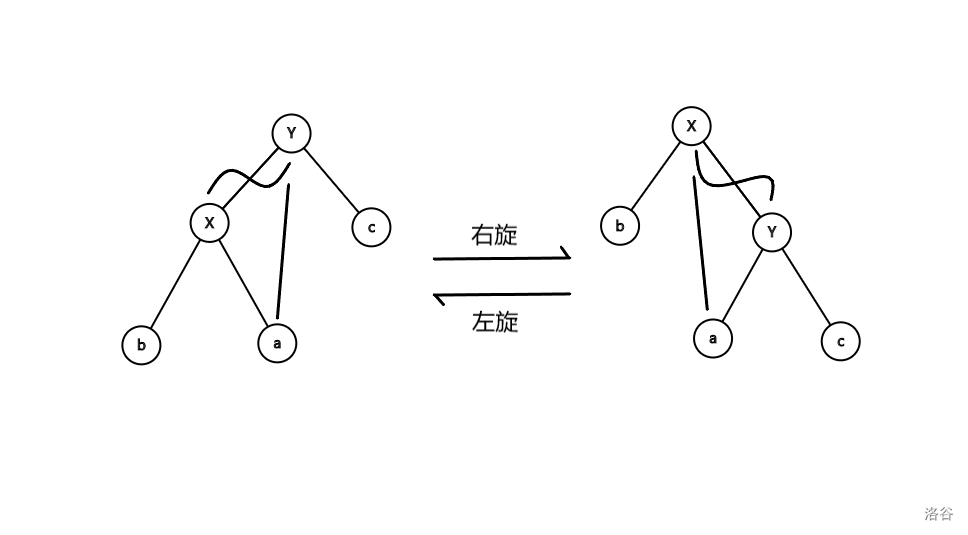
我们右旋\(X\)到其祖先\(Y\)时(设\(X=P\),\(Y=P_1\)):
-
对于\(X\)的右节点\(a\),我们可以得出原来的关系是\(X<a<Y\),所以我们要把\(a\)指向\(Y\),作为其左子节点(先将\(X\)的子节点flip上去,也就是\(Y\)的左子节点变成\(X\)的右子节点);
T[p1].ch[pos]=T[p].ch[pos^1],T[T[p].ch[pos^1]].fa=p1;(\(\texttt{pos}\)在这里是相对的) -
显然\(X\)原来的左子节点仍然在\(X\)的左边,\(Y\)的右子节点仍然在\(Y\)的右边;
-
然后让\(Y\)变成\(X\)的右子节点;
T[p].ch[pos^1]=p1,T[p1].fa=p; -
如果还有\(X\)爷爷节点\(Z\)(\(P_2\)),就把本来是\(Z\)子节点的\(Y\)换成\(X\)。
T[p].fa=p2;if(p2)T[p2].ch[p1==T[p2].ch[1]?1:0]=p; -
最后还需要重新维护一下\(X,Y\)两个节点的\(\texttt{siz}\),自然是先维护子节点再维护祖先节点。
UPDATE_size(p1);UPDATE_size(p);
void Rotate(int p)
{
int p1=T[p].fa;
int p2=T[p1].fa;
int pos=POS_ch(p);
T[p1].ch[pos]=T[p].ch[pos^1],
T[T[p].ch[pos^1]].fa=p1;
T[p].ch[pos^1]=p1;
T[p1].fa=p;
T[p].fa=p2;
if(p2)
{
T[p2].ch[p1==T[p2].ch[1]?1:0]=p;
}
UPDATE_size(p1);UPDATE_size(p);
}
伸展
对于\(\text{Splay}\)伸展操作,我们一般\(6\)种情况讨论。
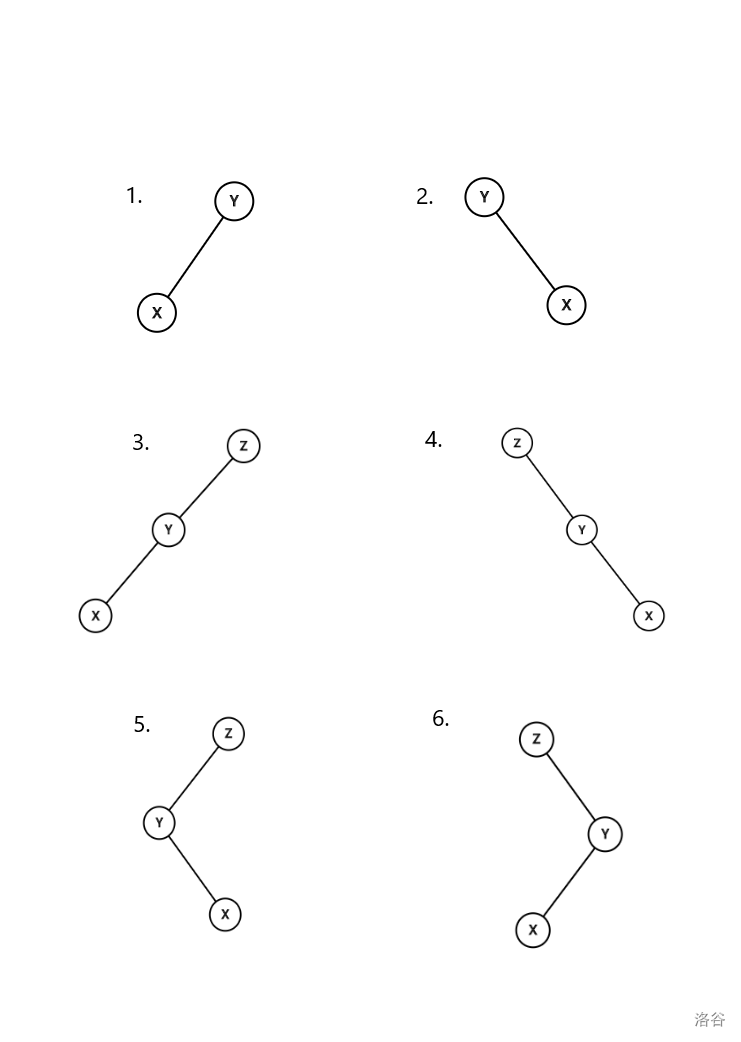
- 对于\(1,2\):\(Y\)就是根节点的情况,我们只需要简单的一次左旋或者右旋;
- 对于\(3,4\):我们称其为三点共线的状态,由于严格符合\(X<Y<Z\) 所以我们只需要将\(Y\)先旋转到\(Z\)的位置,再把\(X\)旋转到上面,这样就把\(X\)旋到根节点了;
- 对于\(5,6\):对于这种情况,我们可以将\(X\)旋转\(2\)次,但是方向不同。
对于这些情况,虽然分类较多,但是代码可以简单处理:
void Splay(int p)
{
for(int i=T[p].fa;i=T[p].fa,i;Rotate(p))//一路往上,旋转p点
{
if(T[i].fa)//如果有爷爷节点
{
int to=(POS_ch(p)==POS_ch(i))?i:p;
//旋转对应的祖先节点,或者2次旋转自身
Rotate(to);
}
}
root=p;
}
以上是根据伸展树性质进行的基本操作,接下来我们对Luogu P3369 【模板】普通平衡树中考察的几种操作进行分析。
\(\texttt{Contents:}\)
- 插入
- 查询: Kth element | Rank of X | 前驱 | 后继
- 删除
- 合并
- 分割
插入
插入操作与一般\(\text{BST}\)的插入大同小异,如果找到了有\(k\)值的节点,就直接将节点大小加一,并且往上不断维护,并且记得Splay(now);
并且记住,第一个插入的点显然要新开一棵树,所以特判如果cnt==0或者!root就直接插入一个值;
如果没有找到有\(k\)权值的节点,那就找到一个\(k\)可以插入的空节点位置,新建节点,也要记得Splay(now);
每次操作都需要UPDATE_size()。
void INS(int k)
{
if(!root)//新树
{
T[++cnt].val=k;
T[cnt].tot++;
root=cnt;
UPDATE_size(cnt);
return ;
}
int now,fanow;
now=root,fanow=0;
while(1)
{
if(T[now].val==k)//找到k
{
T[now].tot++;
UPDATE_size(now);UPDATE_size(fanow);Splay(now);
break;
}
fanow=now;
if(T[now].val<k)//往下找k应该在的节点位置
{
now=T[now].ch[1];
}
else now=T[now].ch[0];
if(!now)//如果到了一棵空子树,新建
{
T[++cnt].val=k;
T[cnt].tot++;
T[cnt].fa=fanow;
T[fanow].ch[T[fanow].val<k]=cnt;
UPDATE_size(cnt);
UPDATE_size(fanow);
Splay(cnt);
break;
}
}
}
查询 Kth element
很显然,一个\(\text{BST}\)的升序排名是根据其中序遍历决定的。
那么很显然,如果这个排名\(\leq\)左子树的大小,那么这个元素必然在左子树内,因为升序序列中越前面的元素越靠左边。
我们从根节点出发开始找,分\(2\)种情况一路往下:
k<=T[T[now].ch[0]].siz我们就一路向左;k>T[T[now].ch[0]].siz就开始扭头向右,然后将k-=T[now].tot+T[T[now].ch[0]].siz;并且将该右子树的根节点作为起点继续遍历。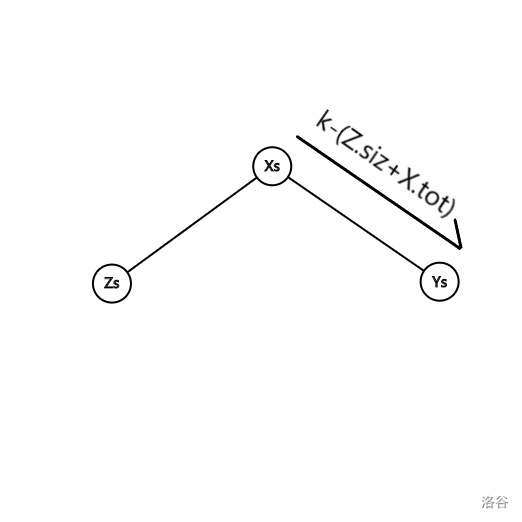
int NOK(int k)//No.k
{
int now=root;
while(1)
{
if(T[now].ch[0]&&k<=T[T[now].ch[0]].siz)
{
now=T[now].ch[0];
}
else
{
k-=T[now].tot+T[T[now].ch[0]].siz;
if(k<=0)
{
Splay(now);//记得Splay(now);哦~
return T[now].val;
}
now=T[now].ch[1];
}
}
}
查询 Rank of k
与\(\texttt{Kth element}\)类似,我们也是从根节点开始,左右判断并查询\(k\)。
向右的时候,由于是排名,所以是加上左子树和根节点的大小,让排名更加靠后。
需要注意排名增加的顺序,因为我们算排名,如果这个数出现多次,我们是以第一次出现的次序当作排名。
如1 2 3 4 5 5 5 5那么5的排名是5而不是6或7或8。
于是乎,如果向右遍历每次先判断是否为\(k\)如果是就返回之前的元素个数\(+1\),如果不是再加上节点大小(tot)。
int Ranking(int k)
{
int rk=0,now=root;
while(1)
{
if(k<T[now].val)
{
now=T[now].ch[0];
}
else
{
rk+=T[T[now].ch[0]].siz;
if(k==T[now].val)
{
Splay(now);//这个也要记得Splay(now);
return rk+1;
}
rk+=T[now].tot;
now=T[now].ch[1];
}
}
}
前驱|后继
- 前驱:小于\(x\)的最大的那个数;
- 后继:大于\(x\)的最小的那个数。
我们先要知道一个性质,对于平衡树上的一个节点,其左子树的最右边的节点就是其前驱,反之为其后继。
那么我们可以用一个很巧妙的方法查询任意值\(x\)的前驱后继。
直接插入\(x\),由于插入后Splay()了,\(x\)已经在根节点了,就可以一路找到底了。
前驱:
int PreMX()
{
int now=T[root].ch[0];
while(T[now].ch[1])now=T[now].ch[1];
Splay(now);//还是记得Splay(now);
return now;
}
后继:
int NxtMX()
{
int now=T[root].ch[1];
while(T[now].ch[0])now=T[now].ch[0];
Splay(now);
return now;
}
删除
我们可以抽象地想象一下,如果有一棵树,然后我们要直接删掉中间层的一个节点,类似于直接扯下来。那么整棵树会错乱散开,我们还需要一直往上UPDATE_size();,所以很麻烦。于是我们在删除一个节点时,我们可以先把这个节点Splay()一下移到根节点位置,进行如下操作。
- 如果说这个节点出现多次\(tot>1\)那么直接
tot--; - 如果说只有一次,那就删掉这个节点,这样可以引用最早看起来一次没用过的整块销毁
DEL_all(); - 然后再把两颗子树合并起来,关于子树的合并操作,后面会有提到。
void DEL_one(int k)
{
int go=Ranking(k);//随便调用一下把k移到根节点
if(T[root].tot>1)
{
T[root].tot--;
UPDATE_size(root);
return ;
}
if(!T[root].ch[0]&&!T[root].ch[1])//删了这个,整棵树都没了
{
DEL_all(root);
root=0;
return ;
}
if(!T[root].ch[0])//只剩下右
{
int now=root;
root=T[now].ch[1];
T[root].fa=0;
DEL_all(now);
return ;
}
if(!T[root].ch[1])//只剩下左
{
int now=root;
root=T[now].ch[0];
T[root].fa=0;
DEL_all(now);
return ;
}
int now=root;int x=PreMX();
T[T[now].ch[1]].fa=x;
T[x].ch[1]=T[now].ch[1];
DEL_all(now);
UPDATE_size(root);//这是合并操作
}
合并
如果要合并两颗子树,那么我们先要保证其中一棵子树的所有元素均小于另一棵的。
我们设更小的是\(L\),更大的是\(R\)。
- 我们伸展\(L\)树,使其最大节点到根节点位置,显然\(L\)树的最大节点还是小于\(R\)中所有元素。
- 那么直接将\(R\)的根节点接上\(L\)的右子树区域,因为显然\(L\)树的最大节点右子树必然为空。而\(R\)子树也不需要特殊操作,因为必定符合性质。
代码可以见删除操作中最后一段。
分割
分割就是将一棵树分为两颗树,一般来说分割操作会给你值\(x\)要求给出比\(x\)大的值和比\(x\)小的。
那么很显然我们需要伸展这颗树,将\(x\)移到根节点,然后直接分割出左子树或右子树即可。
代码可以通过前驱后继辅以实现。类似于合并。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#define N 100005
using namespace std;
int root,cnt;
struct Rey
{
int val;
int fa;
int ch[2];
int siz,tot;
}T[N<<4];
void UPDATE_size(int p){T[p].siz=T[T[p].ch[0]].siz+T[T[p].ch[1]].siz+T[p].tot;}
void DEL_all(int p){T[p].ch[0]=T[p].ch[1]=T[p].fa=T[p].siz=T[p].val=T[p].tot=0;}
int POS_ch(int p){return p==T[T[p].fa].ch[1]?1:0;}
void Rotate(int p)
{
int p1=T[p].fa;
int p2=T[p1].fa;
int pos=POS_ch(p);
T[p1].ch[pos]=T[p].ch[pos^1],
T[T[p].ch[pos^1]].fa=p1;
T[p].ch[pos^1]=p1;
T[p1].fa=p;
T[p].fa=p2;
if(p2)
{
T[p2].ch[p1==T[p2].ch[1]?1:0]=p;
}
UPDATE_size(p1);UPDATE_size(p);
}
void Splay(int p)
{
for(int i=T[p].fa;i=T[p].fa,i;Rotate(p))
{
if(T[i].fa)
{
int to=(POS_ch(p)==POS_ch(i))?i:p;
Rotate(to);
}
}
root=p;
}
void INS(int k)
{
if(!root)
{
T[++cnt].val=k;
T[cnt].tot++;
root=cnt;
UPDATE_size(cnt);
return ;
}
int now,fanow;
now=root,fanow=0;
while(1)
{
if(T[now].val==k)
{
T[now].tot++;
UPDATE_size(now);UPDATE_size(fanow);Splay(now);
break;
}
fanow=now;
if(T[now].val<k)
{
now=T[now].ch[1];
}
else now=T[now].ch[0];
if(!now)
{
T[++cnt].val=k;
T[cnt].tot++;
T[cnt].fa=fanow;
T[fanow].ch[T[fanow].val<k]=cnt;
UPDATE_size(cnt);
UPDATE_size(fanow);
Splay(cnt);
break;
}
}
}
int Ranking(int k)
{
int rk=0,now=root;
while(1)
{
if(k<T[now].val)
{
now=T[now].ch[0];
}
else
{
rk+=T[T[now].ch[0]].siz;
if(k==T[now].val)
{
Splay(now);
return rk+1;
}
rk+=T[now].tot;
now=T[now].ch[1];
}
}
}
int NOK(int k)
{
int now=root;
while(1)
{
if(T[now].ch[0]&&k<=T[T[now].ch[0]].siz)
{
now=T[now].ch[0];
}
else
{
k-=T[now].tot+T[T[now].ch[0]].siz;
if(k<=0)
{
Splay(now);
return T[now].val;
}
now=T[now].ch[1];
}
}
}
int PreMX()
{
int now=T[root].ch[0];
while(T[now].ch[1])now=T[now].ch[1];
Splay(now);
return now;
}
int NxtMX()
{
int now=T[root].ch[1];
while(T[now].ch[0])now=T[now].ch[0];
Splay(now);
return now;
}
void DEL_one(int k)
{
int go=Ranking(k);
if(T[root].tot>1)
{
T[root].tot--;
UPDATE_size(root);
return ;
}
if(!T[root].ch[0]&&!T[root].ch[1])
{
DEL_all(root);
root=0;
return ;
}
if(!T[root].ch[0])
{
int now=root;
root=T[now].ch[1];
T[root].fa=0;
DEL_all(now);
return ;
}
if(!T[root].ch[1])
{
int now=root;
root=T[now].ch[0];
T[root].fa=0;
DEL_all(now);
return ;
}
int now=root;int x=PreMX();
T[T[now].ch[1]].fa=x;
T[x].ch[1]=T[now].ch[1];
DEL_all(now);
UPDATE_size(root);
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int opt,x;
scanf("%d %d",&opt,&x);
if(opt==1)
{
INS(x);
}
if(opt==2)
{
DEL_one(x);
}
if(opt==3)
{
int ans=Ranking(x);
printf("%d\n",ans);
}
if(opt==4)
{
int ans=NOK(x);
printf("%d\n",ans);
}
int pp;
int ans;
if(opt==5)
{
INS(x);
pp=PreMX();
ans=T[pp].val;
DEL_one(x);
printf("%d\n",ans);
}
if(opt==6)
{
INS(x);
pp=NxtMX();
ans=T[pp].val;
DEL_one(x);
printf("%d\n",ans);
}
}
return 0;
}
Splay实现文艺平衡树(区间翻转)
施工中/youl /kk ~
Reference:
- \(\text{OI Wiki}\) - Splay部分
- \(\text{Wikipedia}\) - Splay Tree


