Luogu P3505 【[POI2010]TEL-Teleportation】
-
P3505 【[POI2010]TEL-Teleportation】
一道图论题,挺考思维的,如果从题目特征切入还是可以得出思路的。
虽然没有看起来那么难,但是还是很有难度的题目的
模拟赛整了这道题,于是特地来写题解报告。
洛谷的题面是直接给出抽象的题目模型,有一说一在bzoj上看时还挺难理解的。
后来才发现1h要换算成60min,亏出题人想得出来这巧妙的思路转换,赞美出题人。
-
Prelude
虽然没有给部分分,我们可以先考虑一些暴力或者错误结论骗分。
暴力可以考虑\(\text{Floyd}\)的思路或者直接跑\(\text{Dijkstra}\)记录dist全源最短路,然后点与点两两匹配。
或者跑贪心,尽量拿远的点匹配,如果已经不存在更优情况了就结束贪心。
这都是看到这种建边题可能会口胡出的思路。
那么我们来考虑思维过程。
首先,为什么特地要挑选长度至少为\(5\)呢,为什么不为\(6\),不为\(114514\),边为什么不带权呢。
题目要求输出最大能建的边数,一个一个加自然不可能。那么什么情况下可以快速计算出总数呢。我们可以考虑集合与容斥的思路。
-
Solution
对于图论题,我们如何在图上划分出多个集合呢。我们可以考虑把图分层。
而对于这题就相对比较清楚了。
我们可以把图就分为5层。第一层为点1而最后一层为点2。与1有连边的放第二层,与2有连边的为第4层。那么现在很显然一层一层穿过就已经有了2条边。而中间剩下的那些点该怎么连呢。
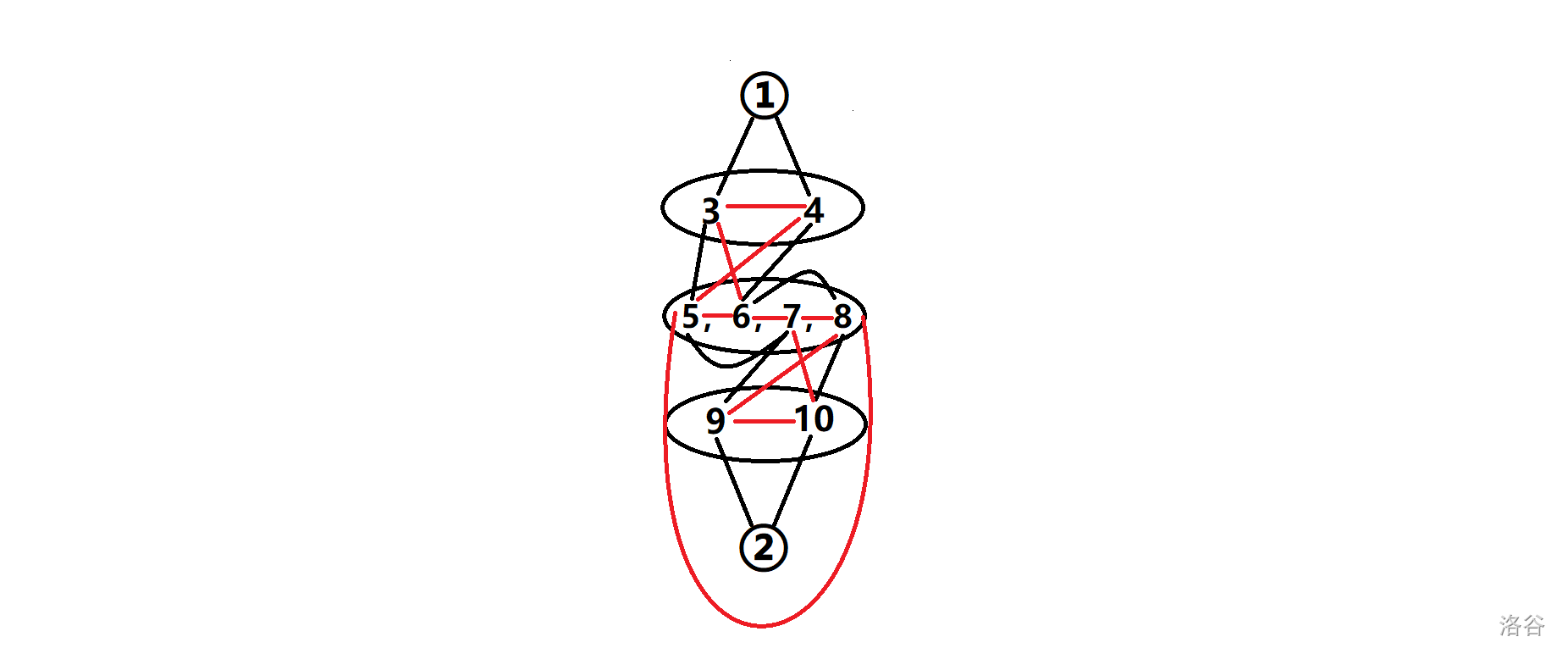
我们给出样例的图示(略丑)。红边是可以新建的而黑色的是本来就有的。
考试时我们也可以自己手造几个小数据推一下找找感觉。
首先我们很清楚每一层的边之间都可以互相连边。因为是一层一层传过,所以层内加边只会增加距离。
其次只有相邻的层的点之间可以连边,不然距离必然缩短至5以内。可以反证证明。
考虑第三层的边,第三层的边一共有3种。
-
与第二层有连边的点;
-
与第四层有连边的点;
-
只与层内点相连的点或者没有任何连边的点。
我们发现,对于与第二层有连边的点,我们不能将其与第四层直接连边,不然必然出现第一层\(\rightarrow\)第二层\(\rightarrow\)第三层\(\rightarrow\)第四层\(\rightarrow\)第五层的长度4的路径。第二种同理。
亦可以理解为,当一条路径走过第三层的点时,我们要保证必须在第三层层内也走一次。所以第三层不存在同时连第二四层的点。
如何保证答案最大化呢。
我们只需要保证:
-
每一层内的点都两两相连
-
对于第三层已经与第二层相连的点将其与第二层所有点都连一遍。
-
对于第三层已经与第四层相连的点将其与第四层所有点都连一遍,
这样思路就出来了,我们的程序只需要及时计数就行。
-
Code
对于这一题思路不好想,但是思路出来程序实现不难,但是由于需要保证不重复计数。代码实现细节并不是很简单。
具体见代码
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 400005
using namespace std;
struct Rey
{
int nxt,to;
}e[N*10];
int head[N],cnt;
int n,m,sec1,sec2,sec3;
int secs[N];
void add(int u,int v)
{
e[++cnt].nxt=head[u];
e[cnt].to=v;
head[u]=cnt;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d %d",&x,&y);
add(x,y);add(y,x);
}
for(int i=head[1];i;i=e[i].nxt)
{
int go=e[i].to;
secs[go]=1;
sec1++;
}//第二层
for(int i=head[2];i;i=e[i].nxt)
{
int go=e[i].to;
secs[go]=2;
sec2++;
}//第四层
sec3=n-sec1-sec2-2;//第三层
int l1,l2;
l1=sec1;
l2=sec2;
int ans=0;
for(int i=3;i<=n;i++)
{
if(!secs[i])//属于第三层
{
ans+=--sec3;
int been;
int tot;
been=tot=0;
//been记录这个点是否已经连了第二层或是第四层
//tot记录如果连了,连了多少条,这样记录答案不需要重复加上
for(int j=head[i];j;j=e[j].nxt)
{
int go=e[j].to;
if(secs[go])tot++,been=secs[go];//是否与2,4层相连
else
{
if(go>i)ans--;//防止重复计数!go>i就是说明这个边之前有连
}
}
if(been==1)ans+=sec1-tot;
if(been==2)ans+=sec2-tot;
if(been==0)ans+=max(sec1,sec2);//都没连,就往多的那一层连
}
else
{
if(secs[i]==1)ans+=--l1;
if(secs[i]==2)ans+=--l2;
//--l1,--l2都是因为这个点连了以后,后面别的点再加答案就不需要考虑他了。
for(int j=head[i];j;j=e[j].nxt)if(secs[e[j].to]&&e[j].to>i)ans--;//同理
}
}
printf("%d\n",ans);
return 0;
}


