Luogu P1262 【间谍网络】
-
P1262 【间谍网络】
Pre芝士\(of\) \(Tarjan\),下方也有引用的:\(\text{My Blog}\)
-
Prelude
题目给了你一个有向图,一个有环,而且只有部分点有点权,部分点没有的一个有向图。你现在使用点\(N\)点权值大小的代价可以进行:将这个点以及这个点可以到达的所有点放入点集\(\mathbf E\)中的操作,保证在点集\(\mathbf E\)中的所有点能到达的点也都在\(\mathbf E\)。
如果
则保证
那么问将所有点放入点集\(\mathbf E\)的最小代价是多少。如果不能输出\(\text{NO}\)以及无法放入的点中最小的那个,可以则输出\(\text{YES}\) & 最小代价。
我们先对题目细节进行分析:
首先是有向图。
如果\(A\)可以购买,\(A\)可以到\(B\),那么花费\(Value_A\)可以使得\(\left\{A,B\right\} \subseteq \mathbf E\),可是不保证买下\(B\)就有\(A\)或者说B可能根本无法单独获取。
那么很显然我们不能点对点分析了,这样不能保证获得最小代价也不能保证复杂度优秀。
既然不能点对点分析,我们就考虑对于这题图的特性。
首先我会想到跑类似点权最短路的东西,但是似乎无法实现,因为如果存在不可到达的点,并不能很好判断,而且在跑最短路时我们如果将没有点权的点贪心为0,那么无法继续程序。稍微改下思路,这样反而变成一个裸的DFS,复杂度与实现难度变得奇奇怪怪。
不过既然想到所谓点权最短路,那么我们就可以考虑到,对于点权最短路,我们必须考虑是否\(\text{DAG}\),不是\(\text{DAG}\)就不能完美实现记忆化搜索等点权计算的操作。毕竟点不是有向边,对于点来说很可能会陷入死循环。
-
Solution
结合以上信息,我们突然想到一个模板涵盖以上特点:P3387 【模板】缩点。
还没学\(Tarjan\)的同学,欢迎来踩\(\text{My Blog}\)
如果我们对这题进行缩点,大部分问题就迎刃而解。
-
对于每个缩点前的强连通分量,我们保证内部点互相通达,这样买了其中一个点,根据前面题意,保证所有强联通分量中的点都在\(\mathbf E\)中。
-
其次,\(Tarjan\)算法可以很好解决输出\(\text{NO}\)的情况。缩点后的图不再有强连通分量,成为一个\(\text{DAG}\),那么怎样都的无法获得点就显而易见,对于这一题,记住并不是那些强连通分量内没有能购买的点就不能获得,如果缩点后的\(N_1 \rightarrow N_2\),即使\(N_2\)中没有点能购买,那么\(N_2\)还是可以通过“购买\(N_1\)中最便宜的那个点”这个操作来获取。简而言之,缩点后我们还是要走一遍该\(\text{DAG}\)来寻找点与点之间的相通性获得最优值。这个情况下最简单的做法自然是DFS,变成DAG后DFS的可行性变得更高。
对于这个题,缩点后的处理才是更为精髓的部分。
-
Code
我写这篇题解其实是因为对于我自己的做法,我很吃惊居然AC了,先缩点,缩点时记得记录这个强连通分量内最便宜的那个,如果没有能买的也要记录一下“-1”为不能买的。
我在缩完点后,干脆对每一个点做DFS,能走的点尽量走,DFS时顺便记忆化该点是否走过,如果走过则不再DFS。就直接从第一个点开始枚举,判断2点:1是是否有能购买的,没有你DFS也没用,有的话还要看之前的点是否涵盖他了。
这个很离谱对吧,真的很离谱,因为他是错的,他只有\(92pts\)(就这还92啊)
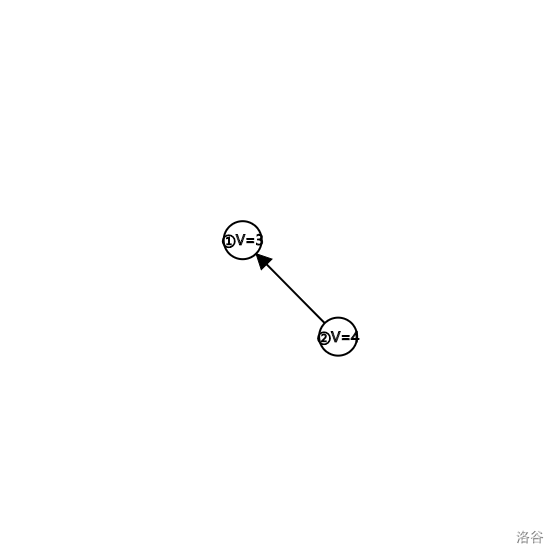
对于这种情况,很明显只需要买2就只需\(Val=4\)一石二鸟,但我for循环从1开始DFS我就会先买1在买2导致\(Val=7\)。
然后我想了想。。。想了想。我想到可以换每个点都做一次起点,但那样貌似T了。
然后我常识性地把他倒着循环了一遍然后再做,取最小的那个。
就A了。所以就惊了并且摸了(指不再深究)。
\(\text{NO}\)的情况详见代码。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<stack>
#define N 300005
using namespace std;
int n,p,r;
int val[N],dfn[N],low[N],tot,cnt,sec[N],secs,size[N],head[N],rtsec[N],head1[N],x[N],y[N];
int ans;
stack <int> s;
bool in[N],oksec[N];
struct Rey
{
int nxt,to;
}e[1000005],e1[1000005];
void add(int u,int v)
{
e[++cnt].nxt=head[u];
e[cnt].to=v;
head[u]=cnt;
}
void add1(int u,int v)
{
e1[++cnt].nxt=head1[u];
e1[cnt].to=v;
head1[u]=cnt;
}
void Tarjan(int x)
{
dfn[x]=low[x]=++tot;
in[x]=1;s.push(x);
for(int i=head[x];i;i=e[i].nxt)
{
int go=e[i].to;
if(!dfn[go])
{
Tarjan(go);
low[x]=min(low[x],low[go]);
}
else if(in[go])low[x]=min(low[x],dfn[go]);
}
if(dfn[x]==low[x])
{
int tp;
secs++;
rtsec[secs]=1<<30;
do
{
tp=s.top();
s.pop();
sec[tp]=secs;
size[secs]++;
in[tp]=0;
if(val[tp]!=-1)
rtsec[secs]=min(rtsec[secs],val[tp]);
}while(x!=tp);
}
}//Tarjan缩点模板,详见另一篇学习笔记。
void DFS(int u)
{
if(oksec[u]==1)return;
oksec[u]=1;
for(int j=head1[u];j;j=e1[j].nxt)
{
int go=e1[j].to;
if(!oksec[go])
DFS(go);
}
}//DFS一直走并记录走过的。
int main()
{
scanf("%d",&n);
scanf("%d",&p);
memset(val,-1,sizeof(val));
memset(rtsec,-1,sizeof(val));
for(int i=1;i<=p;i++)
{
int x;
scanf("%d",&x);
scanf("%d",&val[x]);
}
scanf("%d",&r);
for(int i=1;i<=r;i++)
{
scanf("%d %d",&x[i],&y[i]);
add(x[i],y[i]);
}
for(int i=1;i<=n;i++)
{
if(!dfn[i])Tarjan(i);
}
cnt=0;
for(int i=1;i<=r;i++)
{
if(sec[x[i]]!=sec[y[i]])
{
add1(sec[x[i]],sec[y[i]]);
}
//缩点完也要重新建图,因为缩点后虽然没有环或者强联通分量,
//但是存在买整个强连通分量同时获得另一个的情况。
}
for(int i=1;i<=secs;i++)
{
if((rtsec[i]!=-1&&rtsec[i]!=1<<30)&&oksec[i]==0){DFS(i);ans+=rtsec[i];}//DFS
}
bool ok=1;
int outw=n+1;
for(int i=1;i<=secs;i++)
{
if(!oksec[i])
{
if(ok==1)
{puts("NO");ok=0;}//仍然没走的就一定是NO
for(int j=1;j<=n;j++)
{
if(sec[j]==i&&val[j]==-1)
{
outw=min(outw,j);//找最小的
}
}
}
}
if(ok==0)
{
printf("%d\n",outw);
return 0;
}
int tmp=ans;
ans=0;
memset(oksec,0,sizeof(oksec));
for(int i=secs;i>=1;i--)
{
if((rtsec[i]!=-1&&rtsec[i]!=1<<30)&&oksec[i]==0)
{DFS(i);ans+=rtsec[i];}
}//倒着来一遍
ans=min(ans,tmp);
printf("YES\n%d\n",ans);
return 0;
}
可能是数据比较水,如果有大佬可以Hack掉我会很感激并优化题解和代码。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号