Pascal's Triangle II

Given an index k, return the k^th row of the Pascal's triangle.

For example, given k = 3,
Return [1,3,3,1].

Note:
Could you optimize your algorithm to use only O(k) extra space?

 

A Formula for Any Entry in The Triangle

In fact there is a formula from Combinations for working out the value at any place in Pascal's triangle:

It is commonly called "n choose k" and written like this: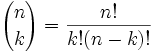

So Pascal's Triangle could also be an "n choose k" triangle like this: (Note how the top row is row zero and also the leftmost column is zero)

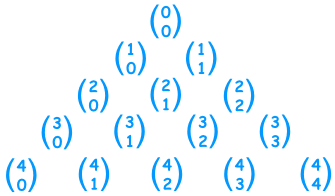
This can be very useful ... you can now work out any value in Pascal's Triangle directly (without calculating the whole triangle above it).Example: Row 4, term 2 in Pascal's Triangle is "6" ...

... let's see if the formula works:

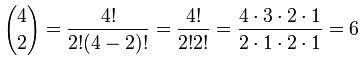
Yes, it works! Try another value for yourself.

public class Solution {
    public ArrayList<Integer> getRow(int rowIndex) {
        // IMPORTANT: Please reset any member data you declared, as
        // the same Solution instance will be reused for each test case.
        ArrayList<Integer> result = new ArrayList<Integer>();
        for(int i = 0; i <= rowIndex; i ++){
            result.add(items(rowIndex, i));
        }
        return result;
    }
    public int items(int m, int n){ // m!/ (n!(m-n)!)
        int i = m;
        long ret = 1;
        for (int j = 1; j <= n; j ++){
            ret *= i --;
            ret /= j;
        }
        return (int)ret;
    }
}

注意的地方是ret要用long，用int会溢出。