最近在刷leetcode,会将一些比较常用的算法整理归纳一下;
双指针法:
以一道题为例(leetcode 第26题);
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。 不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。 给定数组 nums = [1,1,2], 函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 你不需要考虑数组中超出新长度后面的元素。
解法:
1、要求在“原地修改数组”,意味直接修改原有输入数组,不能增加拷贝动作;
2、所以很容易想到, 对于一串数字 1 1 2 2 3 3 4 4......... 将重复的1 剔除掉,之后2放到1的位置上,同理重复的2剔除掉,3放到重复的2位置上;
3、因此,可以抽象的理解为 构造一个新的数组,只不过这个数组的和原来空间一致, 并且他的值都来源于原数组;
需要一个指针去一个个赋值新的数组,又需要一个指针去寻找原数组里的值,所谓双指针;想到这里解法就很简单了
class Solution { public int removeDuplicates(int[] nums) { int i = 0; for(int j = 1; j < nums.length; j++) { if(nums[j] != nums[i]) { i++; //i表示了新数组的长度 nums[i] = nums[j]; } } return i+1; } }
优点: 避免了new一个新的数组,很好的降低了空间复杂度;
再举一个栗子(leetcode的第11题):
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
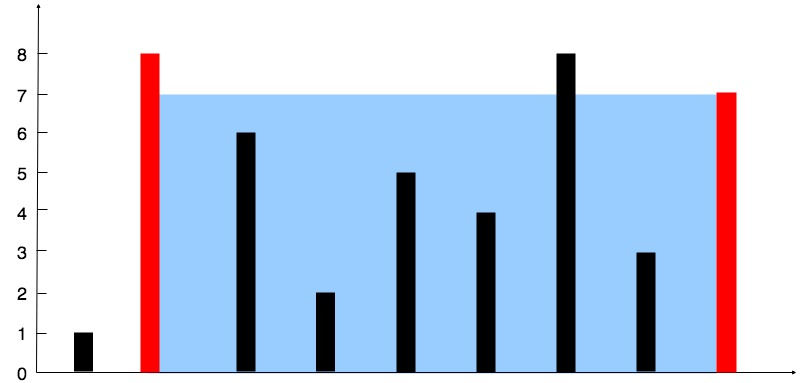
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。 示例: 输入: [1,8,6,2,5,4,8,3,7] 输出: 49
一:当然可以通过遍历法找出所有的组合中的最大面积, 然而时间复杂度为 O(n^2),代码的性能也较差;
二:双指针法:
双指针法具体如何去使用可以从以下几个方面去考虑
(1)i,j指针的初始值及其代表的实际含义;
(2)i,j指针各自如何变化能够保证 可以收敛,所有可能被遍历到 且 趋向于找到最优解法;
因此,映射到上题可以这样考虑:
(1)i,j 初始化为0和n-1两个位置
(2)为了找到一个更优的解,将i,j中更小的数向中间移动才能保证新的解有可能更大;直到i和j相遇,寻找结束;
实现代码为:
class Solution {
/*又是一道双指针的题目*/
public int maxArea(int[] height){
int length = height.length;
int rightIndex = length - 1, leftIndex = 0;
int maxWater = 0;
while(rightIndex > leftIndex)
{
maxWater = Math.max(maxWater,(rightIndex - leftIndex)*((height[rightIndex] >= height[leftIndex]) ? height[leftIndex]: height[rightIndex]));
if(height[leftIndex] <= height[rightIndex])
{
leftIndex++;
}
else
rightIndex--;
}
return maxWater;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号