后缀数组

后缀数组

先下几个常见的定义

\(s(i, j)\)表示\([i, j]\)形成的连续子串

\(suf[i]\)表示以\(i\)为开头的后缀

\(rank\)数组：\(rank[i]\)表示将\(1\sim n\)的后缀排序后，\(suf[i]\)的排名

\(sa\)数组：\(sa[i]\)表示将\(1 \sim n\)的后缀排序后，排第\(i\)的在哪里

举个例子：

sort(a + 1, a + n + 1, cmp);

当我们采用上述代码之后，\(a\)数组存下的实际就是排第\(i\)的在哪里

---

\(sa\)数组不会相同，因为后缀的长度互不相同

在假想状态下，我们考虑在字符串的某尾加上无限个\(0\)

这样子，我们可以使得两个后缀具有相同的长度，便于比较

比如字符串"\(abaa\)"

我们实际上是在比较这4个字符串的排名：

\(abaa，baa0，aa00，a000\)

---

先看一个有趣的事情：
对于字符串\(S = S_1 + S_2, T = T_1 + T_2\)，且\(|S_1| = |S_2|, |T_1| = |T_2|\)
如果\(S_1 < T_1\)，那么\(S < T\)
如果\(S_1 = T_1\;and\;S_2 < T_2\)，那么\(S < T\)

---

这要怎么利用呢？

也就是说，我们现在把所有的后缀都看做是长度为\(n\)的字符串

我们先处理出所有的\(s(i, i)\)的字典序排名，如果不存在\(s(i, i) = s(j, j)\)，那么我们的序排好了

否则，我们可以利用所有的\(s(i, i)\)，按照上面的排序方式，得出所有的\(s(i, i + 2^1 - 1)\)的字典序排名

同样，如果不存在\(s(i, i + 2^1 - 1) = s(j, j + 2^1 - 1)\)，那么我们的序就排好了

否则，合并出\(s(i, i + 2^2 - 1)\)，然后再去判断

依次类推

当我们合并到\(s(i, i + 2^k - 1)\;(2^k \geq n)\)时，我们一定能判断出字典序排名

如果合并的时候，我们的复杂度可以做到\(O(n \log n)\)，那么总体而言，就能做到\(O(n \log ^2 n)\)

如果合并的时候，我们能做到\(O(n)\)，那么总体而言，就能做到\(O(n \log n)\)

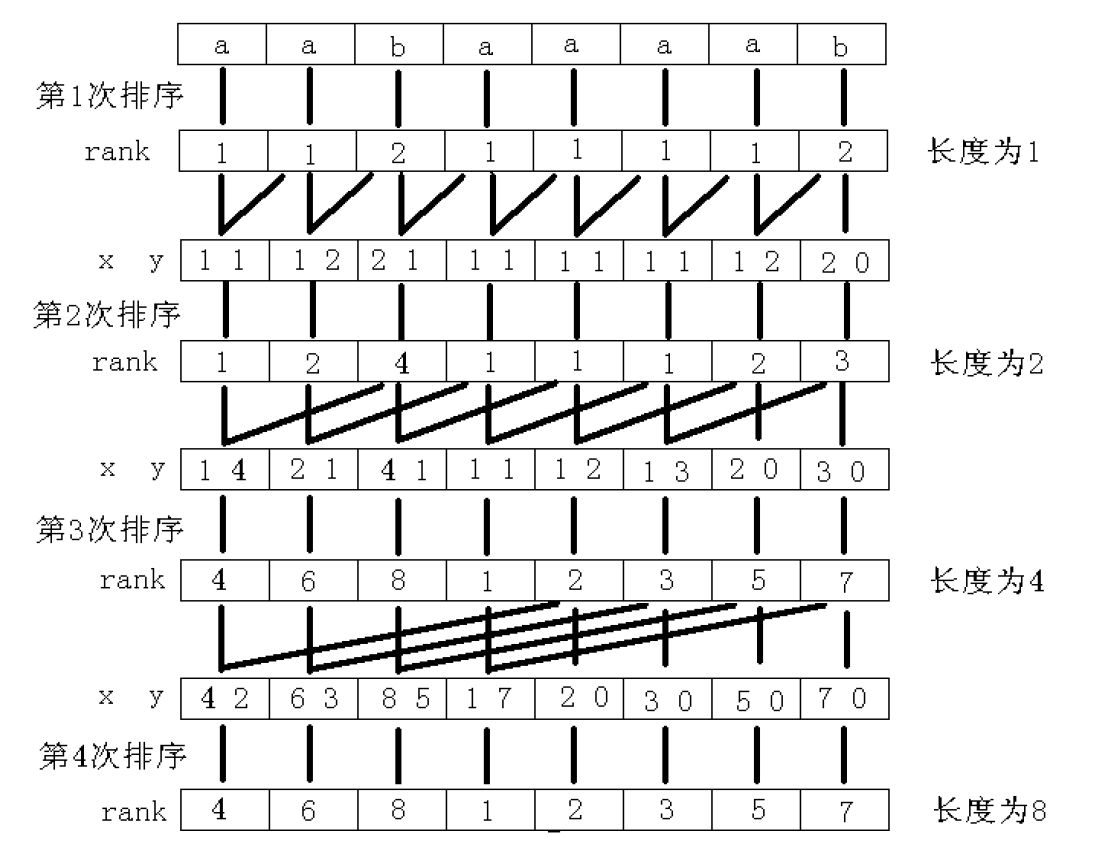
可以对着上面这张经典的图理解一下

---

在描述\(O(n \log n)\)的鬼畜写法之前，我们先来看看\(O(n \log^2 n)\)的写法

inline bool cmp(int x, int y) { return P[x] < P[y]; }
inline void Suffix_sort() {
    for(int i = 1; i <= n; i ++) sa[i] = i;
    for(int i = 1; i <= n; i ++) rk[i] = s[i];
    //初始化sa和rank
    for(int k = 1; k <= n; k <<= 1) {
        //倍增
        for(int i = 1; i <= n; i ++) 
            P[i] = make_pair(rk[i], rk[i + k]);
        //通过stl的pair+sort来实现双关键字排序
        sort(sa + 1, sa + n + 1, cmp);
        int tmp = 1; rk[sa[1]] = 1;
        for(int i = 2; i <= n; i ++)
            rk[sa[i]] = (P[sa[i]] == P[sa[i - 1]]) ? tmp : ++ tmp;
        //排完序之后，按照字典序的顺序对每个点重新计算rank
        if(tmp >= n) break;
        //如果当前的排名已经 >= n，代表不存在两个相同的量，也就是排完了
    }
}

（它在luogu上跑过了1000000）

请确保你在明白了\(O(n \log^2 n)\)的写法后，再继续往下阅读

我们只需要把上面的\(sort\)换成基数排序即可

基数排序原理十分的好懂，请自行了解

void sort(int *a, int n, int m) {
    for(int i = 1; i <= n; i ++) cnt[p2[i]] ++;
    for(int i = 1; i <= m; i ++) cnt[i] += cnt[i - 1];
    for(int i = 1; i <= n; i ++) b[cnt[p2[i]] --] = i;
    //b用来暂时存储对第二关键字排完序之后的结果
    for(int i = 0; i <= m; i ++) cnt[i] = 0;
    for(int i = 1; i <= n; i ++) cnt[p1[i]] ++;
    for(int i = 1; i <= m; i ++) cnt[i] += cnt[i - 1];
    for(int i = n; i >= 1; i --) a[cnt[p1[b[i]]] --] = b[i];
    //这里一定要倒叙枚举
    for(int i = 0; i <= m; i ++) cnt[i] = 0;
}

inline void Suffix_sort() {
    for(int i = 1; i <= n; i ++) sa[i] = i;
    for(int i = 1; i <= n; i ++) rk[i] = s[i];
    int m = 128; //m初始化为字符集的大小
    for(int k = 1; k <= n; k <<= 1) {
        for(int i = 1; i <= n; i ++) 
            p1[i] = rk[i], p2[i] = rk[i + k];
        sort(sa, n, m);
        int tmp = 1; rk[sa[1]] = 1;
        for(int i = 2; i <= n; i ++)
            rk[sa[i]] = 
            	(p1[sa[i]] == p1[sa[i - 1]] && p2[sa[i]] == p2[sa[i - 1]]) ? 
            		tmp : ++ tmp;
        if(tmp >= n) break;
        m = tmp;
    }
}

---

那么我们能不能进一步优化呢？

当然是可以的，可以发现上面代码中的\(rk, p1, p2\)数组其实只需要保留两个即可

并且，对第二关键字实际上并不需要基排，只需要调用上一次的\(sa\)数组就可以得到结果

然而经过测试，发现在\(10^6\)的数据下只有\(20ms\)的常数差距

因此实际上没有必要学习网上流传的写法...

---

经过这么一段长长的文字，你终于懂了后缀数组，但是给后缀排序有啥用呢？

我们需要引入一个更强大的数组

\(lcp(i, j)\)表示后缀\(i\)和后缀\(j\)的最长公共前缀

\(height\)数组，表示\(lcp(suf[sa[i]], suf[sa[i - 1]])\)，即字典序第\(i\)小和字典序第\(i - 1\)小的最长公共前缀

---

一个十分重要的性质
对于后缀\(suf[i]\)和\(suf[j]\)，满足\(lcp(i, j) = min(height[k])\;(k \in[rk[i] + 1, rk[j]])\)

---

考虑证明：

首先证明，\(lcp(i, j) \leq min(height[k])\;(k \in[rk[i] + 1, rk[j]])\)

我们记\(min(height[k]) = h\)

如果\(lcp(i, j) > h\)，那么对于\(k \in [rk[i] + 1, rk[j]]\)而言

我们记\(lcp(i, j) = L\)

由于\(k\)的排名处于\(i\)和\(j\)之间，并且\(i\)和\(j\)的前\(L\)都相同，必然有\(k\)包含\(L\)这个前缀

否则，\(k\)的排名由于在\(L\)之前就出现了不同，因此要么在\(i\)之前，要么在\(j\)之后

因此，有\(height[k] = L > h = min(height[k])\)

这不可能，因此\(lcp(i, j) \leq h\)

然后证明，可以取到上界

这是因为\(height[i] \geq h\)，可以看做\(suf[sa[i]]\)和\(suf[sa[i - 1]]\)至少有长为\(h\)的公共前缀

公共前缀满足传递性，因此可以取到上界

---

那么怎么求\(height\)数组呢？

如果暴力的求解，复杂度显然是\(O(n^2)\)的

我们可以很清楚的知道\(suf[sa[i]]\)和\(suf[sa[i - 1]]\)在字符串构成的联系不如\(suf[i]\)和\(suf[i - 1]\)的联系

毕竟，\(suf[i]\)和\(suf[i - 1]\)只相差了一个字符

那么，我们直接按照下标顺序来计算的时候，可以发现

---

我们记\(h[i]\)表示\(suf[i]\)和字典序排在它前面的最长公共前缀

那么\(h[i] \geq h[i - 1] - 1\)

比如现在正在求\(h[i]\)，排在\(i\)之前的后缀是\(suf[j]\)

后缀\(i\)为\(abc...\)，后缀\(j\)为\(aba...\)，那么\(h[i] = 2\)

求\(h[i + 1]\)时，由于\(h[i] \geq 1\;(h[i] = 0可以无视)\)

因此，去掉首字母的后缀\(i + 1\)为\(bc...\)，后缀\(j + 1\)为\(ba...\)

可以发现，\(j + 1\)还是保持排在\(i + 1\)的前面，不妨设排在\(i + 1\)前面的后缀为\(k\)

那么，一定有\(h[i + 1] = lcp(i + 1, k) \geq lcp(i + 1, j + 1) = h[i] - 1\)

---

和求后缀数组比起来，求\(height\)显得十分的简洁

void Solve() {
    for(int i = 1, k = 0; i <= n; i ++) {
        if(k) k --; //此时的k相当于h[i]，得到的新k相当于h[i] - 1
        int j = sa[rk[i] - 1];
        while(s[j + k] == s[i + k]) k ++;
        height[rk[i]] = k; // = h[i]
    }
}

由于每次求\(h[i]\)时，\(k\)指针都只会\(- 1\)，也就是增加\(1\)的势能

而每次\(k\)往前挪移的时候，都需要\(1\)的势能

那么，势能总量是\(O(n)\)的，也就是求\(height\)数组只需要\(O(n)\)的复杂度